格的反软理想
童 娟,廖祖华*,赵衍才,2,廖翠萃,张龙祥,路 腾,吴树忠
(1. 江南大学 理学院 信息与计算科学系, 江苏 无锡 214122; 2. 无锡城市职业技术学院 基础课部,江苏 无锡 214153)
格的反软理想
童 娟1,廖祖华1*,赵衍才1,2,廖翠萃1,张龙祥1,路 腾1,吴树忠1
(1. 江南大学 理学院 信息与计算科学系, 江苏 无锡 214122; 2. 无锡城市职业技术学院 基础课部,江苏 无锡 214153)
首先给出了格的反软理想新概念,证明2个反软理想分别在软集的限制并和“或”运算下仍然是反软理想.其次,利用软集的反对偶给出反软理想的等价刻画.再次,利用软集的反扩张原理给出反软理想在同态映射下反像与原像的性质.最后,在全体反软理想组成的集合H上,引入链条件并讨论H是阿丁的或诺特的充要条件.
反软理想;软集;反对偶;同态;反像
Anti-soft ideals of lattices. Journal of Zhejiang University(Science Edition), 2017,44(1):033-039
0 引 言
1999年,MOLODTSOV[1]提出了软集的概念,其理论与模糊集、直觉模糊集、粗糙集等有很强的互补性,主要从参数化角度为研究不确定性问题提供统一的数学框架.后来软集在理论、应用等方面得到迅速发展[2-3].2007年,AKTAS等[4]在软集理论与群论的基础上提出了软群的新概念并研究了其基本性质,由此开创了软集代数研究的新领域.
19世纪末,PEIRCE等提出了格的概念,20世纪30年代BIRKHOFF对格论进行了相关研究[5].格是一种重要的偏序结构,其理论已经深入到数学研究的各个领域[6].2010年,LI[7]基于完备格提出了软格的概念,并讨论了它和模糊软集的关系.2008年,吴广庆[8]给出了格的L-fuzzy素理想的定义,得到了格的L-fuzzy素理想、格的L-fuzzy理想的若干等价刻画.2009~2011年,花秀娟等[9-10]研究了模糊格,给出了格上的(∈,∈∨q)-模糊素理想以及(λ,μ)-模糊子格(理想)的定义,并研究了它们的相关性质.2014年,李京效等[11]把模糊软集理论运用到格上,引入了(λ,μ)模糊软理想并讨论了其相关性质.同年,王德江等[12]给出了R-广义模糊子格理想的定义,并研究了它们的交、并、同态像及原像的相关性质.
1990年,BISWAS[13]引入了群上的反模糊子群,开创了反模糊子代数研究的新领域.2012年,FENG等[14]介绍了反模糊(λ,μ)-子群并研究了其相关性质.2015年,郭二芳等[15]对反模糊子群和反模糊正规子群做了一些研究.
反模糊子集在直觉模糊集上有重要的应用,直觉模糊集的非隶属度是反模糊子集,它在投票问题中可表示投反对票的情况.由于直觉模糊集在投票问题中能很好地刻画赞成人群及反对人群的情况,所以有关直觉模糊集理论及其在决策、逻辑规划、医疗诊断、机器学习和市场预测等领域中的应用研究已引起广泛关注,并取得了丰硕成果[16-17].
吴修竹等[18]提出了反软子半群的概念,由此开创了反软子代数的研究领域,随后,童娟等[19]给出了反软子格的定义,并研究它的一系列性质.
温永川[20]将参数集赋予群的代数结构,提出了一种新型的软群,并研究了其相关性质.廖祖华研究组[21-27]基于他们的思想,将参数集赋予格的代数结构,提出了反软理想这一新的代数结构,并研究了其基本性质.
下文安排如下:第1节给出本文所需的相关知识,第2节给出2个反软理想在软集运算下的性质、等价刻画、原像及反像的性质,第3节在全体反软理想组成的集合H上引入链条件,并讨论H是诺特的或是阿丁的一些基本性质.
1 预备知识
定义1[6]设在一个偏序集(L,≤)中,如果任意两元x,y都有上确界x∨y和下确界x∧y,则称偏序集(L,≤)为一个格.
下文中L表示格.
定义2[6]设L1为格L的一个非空子集,若∀a,b∈L1,总有a∧b∈L1,a∨b∈L1,则称L1为格L的子格.
定义3[20](笛卡尔直积) E1,E2是2个非空集合,称E1×E2={(x,y)|x∈E1,y∈E2}为E1和E2的笛卡尔直积.
定义4[28](格的直积) 设L1和L2是2个格.定义笛卡尔直积L1×L2上的运算:
(x1,y1)∧(x2,y2)=(x1∧x2,y1∧y2),
(x1,y1)∨(x2,y2)=(x1∨x2,y1∨y2).则由格的定义知,(L1×L2;∧,∨)是一个格,称(L1×L2;∧,∨)是格L1和L2的笛卡尔格直积.
定义5[6]设(L,≤)是格,I是L的非空子集且满足:
(1)g1∨g2∈I, ∀g1,g2∈I;
(2)若g2≤g1,则g2∈I, ∀g1∈I,g2∈L.
称I为L的一个理想.
定理1[6]设L是任意格,I是L的非空子集,则下列条件等价:
(1)I是L的理想;
(2)∀g1,g2∈L,g1∨g2∈I的充要条件是g1∈I且g2∈I;
(3)I是L的子格,∀g1∈I,g2∈L,有g1∧g2∈I.
引理1 I是L的非空子集,如果满足下列条件:
(1)∀g1,g2∈I,有g1∨g2∈I;
(2)∀g1∈I,g2∈L,有g1∧g2∈I.
则I是L的理想.
定义6[2]令X是初始全集,E是一个参数集,P(X)表示X的幂集,E1⊆E,F:E1→P(X)为映射,则称(F,E1)为X的软集,也称F是E1的软集.
下文中,X表示初始全集,P(X)表示X的幂集.
定义7[29](软集的限制并) (F,E1),(G,E2)是X的软集,若软集(H,E)满足:
(1)E=E1∩E2≠∅;
(2)∀e∈E,有H(e)=F(e)∪G(e).
则称(H,E)是软集(F,E1)和(G,E2)的限制并,记作(H,E)=(F,E1)∪R(G,E2).
定义8[2](软集的或运算) (F,E1),(G,E2)是X的软集,令(H,E1×E2)=(F,E1)∨(G,E2),其中∀(α,β)∈E1×E2,H(α,β)=F(α)∪G(β),称(H,E1×E2)是(F,E1)与(G,E2)的或运算,并记为(F,E1)∨(G,E2).
定义9[15](扩张原理) 设f:E1→E2为一个映射,H1:E1→P(X)和H2:E2→P(X)均为软集,令:
f-1(H2)(g1)=H2(f(g1)),
则f(H1),f-1(H2)分别为E2,E1上的软集,并称f(H1)为H1的像,f-1(H2)为H2的原像.
定义10[18](反扩张原理) 设f:E1→E2为一个映射,H1:E1→P(X)和H2:E2→P(X)均为软集,令:
f-1(H2)(g1)=H2(f(g1)),
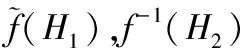


2 格的反软理想
本节引入反软理想的概念,并用实例说明格的反软理想的存在性,同时讨论格的反软理想在软集运算中的等价刻画、反像与原像等性质.
定义13 设H:L→P(X)是一个软集,∀g1,g2∈L,若满足:
(1)H(g1∨g2)⊆H(g1)∪H(g2);
(2)H(g1∧g2)⊆H(g1).
则称H为L的反软理想.
例1 设L={0,a,b,1}是一个四元格,其中a‖b且0≤a,b≤1,取X={x,y,z,w},且H:L→P(X):H(0)=∅,H(a)={y,z},H(b)={x,z},H(1)={x,y,z}.由定义13知,H为L的反软理想.
例1说明了格的反软理想的存在性.
定理2 设L1与L2是L的子格,且L1∩L2≠∅,又设H1与H2分别是L1与L2上的反软理想,则H=H1∪RH2是L1∩L2上的反软理想.
证明 因为L1与L2是L的子格,且L1∩L2≠∅,所以L1∩L2是L的子格,又因为H1,H2分别是L1,L2上的反软理想,∀g1,g2∈L1∩L2,有g1,g2∈Li(i=1,2),故H1(g1∨g2)⊆H1(g1)∪H1(g2),H1(g1∧g2)⊆H1(g1),H2(g1∨g2)⊆H2(g1)∪H2(g2),H2(g1∧g2)⊆H2(g1).所以,
H(g1∨g2)=(H1∪RH2)(g1∨g2)=H1(g1∨g2)∪H2(g1∨g2)⊆(H1(g1)∪H1(g2))∪(H2(g1)∪H2(g2))=(H1(g1)∪H2(g1))∪(H1(g2)∪H2(g2))⊆H(g1)∪H(g2);H(g1∧g2)=(H1∪RH2)(g1∧g2)=H1(g1∧g2)∪ H2(g1∧g2)⊆H1(g1)∪H2(g1)=H(g1).
所以,H=H1∪RH2是L1∩L2上的反软理想.
定理3 设H1,H2分别是L的子格L1,L2上的反软理想,则H=H1∨H2也是L=L1×L2上的反软理想.
证明 由格的直积知L是一个格,∀(g1,g2),(m1,m2)∈L1×L2,则g1,m1∈L1且g2,m2∈L2.因为H1,H2分别是格L1,L2上的反软理想,所以H1(g1∨m1)⊆H1(g1)∪H1(m1),H1(g1∧m1)⊆H1(g1);H2(g2∨m2)⊆H2(g2)∪H2(m2),H2(g2∧m2)⊆H2(g2).因此:
(1)H((g1,g2)∨(m1,m2))=H((g1∨m1),(g2∨m2))=H1(g1∨m1)∪H2(g2∨m2)⊆(H1(g1)∪H1(m1))∪(H2(g2)∪H2(m2))⊆(H1(g1)∪H2(g2))∪(H1(m1)∪H2(m2))=H(g1,g2)∪H(m1,m2);
(2)H((g1,g2)∧(m1,m2))=H((g1∧m1),(g2∧m2))=H1(g1∧m1)∪H2(g2∧m2)⊆H1(g1)∪H2(g2)⊆H(g1,g2).
由(1)、(2),知H=H1∨H2是L=L1×L2上的反软理想.
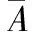
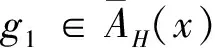
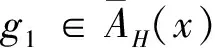
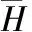
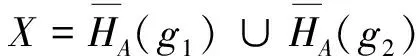
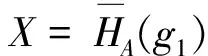
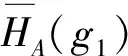
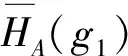
由(1)、(2)知,A(x)为L的一个理想.
定理6 设L1,L2是格,f:L1→L2是同态映射,H1:L1→P(X)是软集,H2:L2→P(X)也是软集.则有:

(2)若H2是L2的反软理想,则f-1(H2)是L1的反软理想.
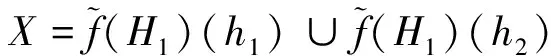
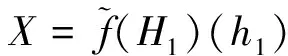
(2)∀g1,g2∈L1,由H2为L2的反软理想,则
f-1(H2)(g1)∪f-1(H2)(g2)=H2(f(g1))∪H2(f(g2))⊇H2(f(g1)∨f(g2))=H2(f(g1∨g2))=f-1(H2)(g1∨g2);f-1(H2)(g1)=H2(f(g1))⊇H2(f(g1)∧f(g2))=H2(f(g1∧g2))=f-1(H2)(g1∧g2).
所以f-1(H2)为L1的反软理想.
定理7 f:L1→L2为格的满同态映射,H2:L2→P(X)为L2的软集,则H2为L2的反软理想的充要条件是f-1(H2)是L1的反软理想.
证明 必要性:由定理6(2)知结论成立.
充分性:(1)∀h1,h2∈L2,若X=H2(h1)∪H2(h2),则H2(h1∨h2)⊆H2(h1)∪H2(h2);若X≠H2(h1)∪H2(h2),因为f是满同态映射,故存在g1,g2∈L1使f(g1)=h1,f(g2)=h2且f(g1∨g2)=f(g1)∨f(g2)=h1∨h2,因为f-1(H2)是L1的反软理想,所以H2(h1∨h2)=H2(f(g1∨g2))=f-1(H2)(g1∨g2)⊆f-1(H2)(g1)∪f-1(H2)(g2)=H2(h1)∪H2(h2),故H2(h1∨h2)⊆H2(h1)∪H2(h2).
(2)∀h1,h2∈L2,因为f是满同态映射,所以存在g1,g2∈L1使得f(g1)=h1,f(g2)=h2,故f(g1∧g2)=f(g1)∧f(g2)=h1∧h2,因为f-1(H2)是L1的反软理想,所以H2(h1∧h2)=H2(f(g1∧g2))=f-1(H2)(g1∧g2)⊆f-1(H2)(g1)=H2(h1),故H2(h1∧h2)⊆H2(h1).
由(1)、(2)知,H2是L2的反软理想.
定义14[20]f:L1→L2是映射,H是L1的软集,∀x,y∈L1,若f(x)=f(y),有H(x)=H(y),则称H是f-不变的.
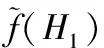
证明 必要性:由定理6(1)知结论成立.
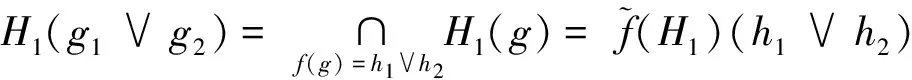

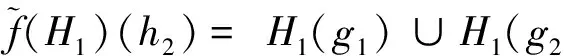
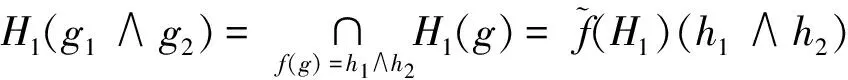

3 反软理想的链条件
本节在反软理想组成的集合H上引入升链及降链条件,并讨论H是阿丁或诺特的充要条件.
定义15 记L上全体反软理想集合为H,在反软理想中定义一个二元关系“≤”:H1≤H2⟺H1(g)⊇H2(g),∀g∈L.
定义16 记L上全体反软理想集合为H,在反软理想中定义一个二元关系“=”:
H1=H2⟺H1(g)=H2(g),∀g∈L.
定理9 定义15中二元关系“≤”是一个偏序,称(H,≤)是一个偏序集.
证明 ∀H1∈H,∀g∈L,因为H1(g)⊇H1(g),所以由定义得H1≤H1;∀H1,H2,H3∈H,若H1≤H2且H2≤H3,由定义∀g∈L,H1(g)⊇H2(g)且H2(g)⊇H3(g),故H1(g)⊇H3(g),所以H1≤H3.∀H1,H2∈H,若H1≤H2且H2≤H1,由定义∀g∈L,H1(g)⊇H2(g)且H2(g)⊇H1(g),故H1(g)=H2(g),所以H1=H2.
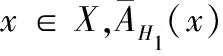

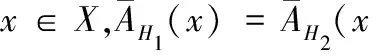
定义17 设H是格的全体反软理想的集合,H中任意元素列{Hi|i=1,2,…}若组成一个降链,即H1≥H2≥…≥Hn≥…,如果存在一个正整数m,使得Hm=Hm+n,n=1,2,…,则称H满足降链条件,或称H为阿丁的.
定义18 设H是L的全体反软理想的集合,H中任意元素列{Hi|i=1,2,…}若组成一个升链,即H1≤H2≤…≤Hn≤…,如果存在一个正整数m,使得Hm=Hm+n,n=1,2,…,则称H满足升链条件,或称H为诺特的.
定义19 Ω(L)表示L的一理想族,对于Ω(L)的任意理想的升链L1⊆L2⊆…⊆Ln⊆…,如果存在正整数n,使得对所有m>n,有Lm=Ln,则称Ω(L)满足升链条件,此时称Ω(L)是诺特的,min{i|Li=Li+1,i=1,2,…}称为{Li}的诺特平稳指数,记为n{Li}.
定义20 Ω(L)表示L的一理想族,对于Ω(L)中任意理想的降链L1⊇L2⊇…⊇Ln⊇…,如果存在正整数n,使得对所有m>n,有Lm=Ln,则称Ω(L)满足降链条件,此时称Ω(L)为阿丁的,min{i|Li=Li+1,i=1,2,…}称为{Li}的阿丁平稳指数,记为a{Li}.



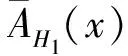
4 结束语
将参数集赋予格的代数结构,给出了反软理想的概念,得到了反软理想在软集运算下的性质及同态性.最后,研究了由反软理想组成的集合H上链条件的相关性质.下一步可以引入并研究格的反软素理想的代数结构.
[1] MOLODTSOV D. Soft set theory-first results[J]. Computers and Mathematics with Applications,1999,37:19-31.
[2] MAJI P K, BISWAS R, ROY A R. Soft set theory[J]. Computers and Mathematics with Applications, 2003,45:555-562.
[3] MAJI P K, ROY A R. An application of soft sets in a decision making problem[J]. Computers and Mathematics with Applications, 2002,44:1077-1083.
[4] AKTAS H, CAGMAN N. Soft sets and soft groups[J]. Information Sciences, 2007,177:2726-2735.
[5] BIRKHOFF G. Lattice Theory[M]. Providence: American Mathematical Society,1961.
[6] 胡长流,宋振明.格论基础[M].开封:河南大学出版社,1990. HU C L, SONG Z M. Lattices Theory Foundation[M]. Kaifeng: Henan University Press,1990.
[7] LI F. Soft lattices[J]. Global Journal of Science Frontier Research,2010,10(4):157-159.
[8] 吴广庆.格的L-fuzzy素理想[J].模糊系统与数学,2008,22(4):63-67. WU G Q.L-fuzzy prime ideals of lattice[J]. Fuzzy Systems and Mathematics, 2008,22(4):63-67.
[9] 花秀娟,朱熙.L-fuzzy格及(λ,μ)-fuzzy凸子格[J].纺织高校基础科学学报,2009,22(4):529-531. HUA X J, ZHU X.L-fuzzy lattice and(λ,μ)-fuzzy convex sublattice[J]. Basic Sciences Journal of Textile Universities, 2009,22(4):529-531.
[10] 花秀娟,辛小龙,刘庆.(∈,∈∨q)-模糊素理想与(λ,μ)-模糊子格(理想)[J].模糊系统与数学,2010,24(4):33-38. HUA X J, XIN X L, LIU Q. (∈,∈∨q)-Fuzzy prime ideal and (λ,μ)-fuzzy sublattice(ideal)[J]. Fuzzy Systems and Mathematics, 2010,24(4):33-38.
[11] 李京效,辛小龙,贺鹏飞.模糊软格与模糊软理想[J].模糊系统与数学,2014,28(2):69-75. LI J X,XIN X L, HE P F. Fuzzy soft lattices and fuzzy soft ideals[J]. Fuzzy Systems and Mathematics, 2014,28(2):69-75.
[12] 王德江,梁久祯,廖祖华.R-广义模糊子格的理[J].计算机科学,2014,41(1):271-274. WANG D J, LIANG J Z, LIAO Z H. Ideal ofR-generalized fuzzy sublattice[J]. Computer Science,2014,41(1):271-274.
[13] BISWAS R. Fuzzy subgroups and anti fuzzy subgroups[J]. Fuzzy Sets and Systems,1990,35(1):121-124.
[14] FENG Y M, YAO B X. On (λ,μ)-anti-fuzzy subgroups[J]. Journal of Inequalities and Applications,2012,78:1-5.
[15] 郭二芳,李玉瑛,王绪柱.反模糊子群的运算[J].数学的实践与认识,2015,45(12):279-284. GUO E F, LI Y Y, WANG X Z. Operations of anti-fuzzy subgroups[J]. Mathematics in Practice and Theory, 2015,45(12):279-284.
[16] ATANASSOV K T. On Intuitionistic Fuzzy Sets Theory [M]. Berlin/Heidelberg: Springer-Verlag, 2012.
[17] BUSTINCE H, HERRERA F, MONTERO J. Fuzzy Sets and Their Extensions: Representation, Aggregation and Models[M]. New York: Springer Publishing Company: Physica -Verlag, 2007.
[18] 吴修竹,廖祖华,刘维龙.反软子半群[J].模糊系统与数学,2015,29(5):44-50. WU X Z, LIAO Z H, LIU W L. Anti-soft subsemigroups[J]. Fuzzy Systems and Mathematics, 2015,29(5):44-50.
[19] 童娟,廖祖华,路腾,等.反软子格[J].模糊系统与数学,2016,30(1):20-27. TONG J, LIAO Z H, LU T, et al. Anti-soft sublattices[J]. Fuzzy Systems and Mathematics,2016,30(1):20-27.
[20] 温永川.关于软集的研究[D].大连:辽宁师范大学,2008. WEN Y C. The Study of Soft Set[D]. Dalian: Liaoning Normal University, 2008.
[21] 赵迪,廖祖华,朱晓英,等.半群的软理想[J].模糊系统与数学,2014,28(4):45-50. ZHAO D, LIAO Z H, ZHU X Y, et al. Soft ideals of semigroup[J]. Fuzzy Systems and Mathematics,2014,28(4):45-50.
[22] 殷霞,廖祖华,朱晓英,等.软集与新型软子群[J].计算机工程与运用,2012,48(33):40-43. YIN X, LIAO Z H, ZHU X Y, et al. Soft sets and the new soft subgroup [J]. Computer Engineering and Applications, 2012,48(33):40-43.
[23] 叶灵军,廖祖华,朱晓英,等.软完全正则子半群[J].工程数学学报,2014,31(3):341-346. YE L J, LIAO Z H, ZHU X Y, et al. Soft completely regular sub-semigroup[J]. Chinese Journal of Engineering Mathematics, 2014,31(3):341-346.
[24] 关贝贝,廖祖华,朱晓英,等.软子半群[J].模糊系统与数学,2014,28(4):39-44. GUAN B B, LIAO Z H, ZHU X Y, et al. Soft subsemigroups[J]. Fuzzy Systems and Mathematics,2014,28(4):39-44.
[25] 叶婷,廖祖华,朱晓英,等.半群的软完全素理想[J].模糊系统与数学,2014,28(3):1-5.YE T, LIAO Z H, ZHU X Y, et al. Soft completely prime ideals of semigroup[J]. Fuzzy Systems and Mathematics,2014,28(3):1-5.
[26] YIN X, LIAO Z H. Study on soft groups[J].Journal of Computers,2013(8):960-967.
[27] ZHENG G P, LIAO Z H, WANG N N, et al. Soft lattice implication subalgebra[J]. Applied Mathematics and Information Sciences,2013,7(3):1181-1186.
[28] 方捷.格论导引[M].北京:高等教育出版社,2014. FANG J. Lattice Theory Guidance[M]. Beijing: Higher Education Press, 2014.
[29] ALI M I, FENG F, LIU X Y, et.al. On some new operations in soft set theory [J]. Computers and Mathematics with Applications, 2009,57(9):1547-1553.
TONG Juan1, LIAO Zuhua1, ZHAO Yancai1,2, LIAO Cuicui1, ZHANG Longxiang1, LU Teng1, WU Shuzhong1
(1.DepartmentofInformationandComputerScience,SchoolofScience,JiangnanUniversity,Wuxi214122,JiangsuProvince,China; 2.DepartmentofBasicScience,WuxiCityCollegeofVocationalTechnology,Wuxi214153,JiangsuProvince,China)
Firstly, the definition of anti-soft ideals is given, and we show that the restricted union and‘OR’operation of two anti-soft lattices are still anti-soft ideal. Then, we discuss the equivalent characterizations of anti-soft ideals based on the anti-dual of soft set. In addition, based on the anti-extension principle, the properties of their anti-image and inverse image are derived under the homomorphic mapping. Finally, we introduce the condition of chain overHwhich is composed of all the anti-soft ideals, and discuss the necessary and sufficient condition for thatHis Artinian or Noetherian.
anti-soft ideal; soft set; anti-dual; homomorphism; anti-image

2015-07-27.
江苏省自然科学基金资助项目(BK20151117);国家自然科学基金资助项目(61673193).
童 娟(1992-),ORCID:http://orcid.org/0000-0002-4049-7803,女,硕士研究生,主要从事软集代数研究.
*通信作者,ORCID:http://orcid:org/0000-0002-7205-664X,E-mail:liaozuhua57@163.com
10.3785/j.issn.1008-9497.2017.01.005
O 159;O 153.1
A
1008-9497(2017)01-033-07

