利用几何画板，助力“二次函数”课堂教学

朱社义

浙江省临安市岛石中心学校

摘 要：几何画板能准确地展现几何图形，揭示几何规律，侧重过程教学，动态地再现数学知识的发生、发展和形成过程，开创了教与学的新方式.几何画板的应用，能最大限度地调动学生思维的积极性和创造性，潜移默化地促使学生自主学习.本文在教学实践的基础上，结合一些典型的教学案例，从选择函数探索图象，分析图象研究性质，函数变换动态演示，观察最值总结规律。四个方面较深入地阐述了几何画板在初中数学教学中的具体应用，从而促进信息技术与数学教学的有效整合，提高教学效率。

关键词：几何画板；二次函数；图象

几何画板将函数图象从纸面上转移到了电子屏幕上来，这样就使图形更加规范，变换更加顺畅，有效的提高了课堂效率。我们所熟知的几何画板通常应用在几何图形的绘制上，在函数图象上的应用体现了几何画板的拓展性。在使用时，要注意到以知识为主，以软件为辅，重点以教师演示为主，不要求学生掌握软件，避免喧宾夺主。下面笔者从四个方面进行阐述。

一、选择函数，探索图象

学过二次函数的人都知道，二次函数的图象是一個抛物线。抛物线的概念学生在生活中也不陌生，二次函数的学习将这个概念搬到了书本上。对于初学者来说，可以从图形和解析式两个方向同时学习，教师建立函数的同时也生成图象，让学生有一个完整的认识。

在教材中，二次函数安排在了九年级上册第一章，自此开始，函数世界的大门真正向学生打开，更加复杂的函数图象也即将与学生们见面。相比于一次函数的图象是一条直线，二次函数中多了一项乘方运算，而函数的变化也更加复杂，[x2]是变量变化的一个积累。那么二次函数的图像又会是怎样？变化规律又会是怎样？它又有哪些性质呢？等一系列问题开始困扰学生。我从一个例子开始给学生演示“同学们，我们现在开始探索二次函数[y=x2-2x+1]图象，很显然在学生还不知道二次函数图象时是很难画出完整图象的，特别是对于最低点，对称性等。如果这时能够借助几何画板，用点[x，x2]，的，轨迹来构造函数图象那就太好了，学生可以一目了然。

很清楚的看出[y=x2]的图象是一条抛物线，函数的最低点是原点，对称轴是[y]轴，以及图象的增减性等。这对学生来说是一个函数的整体印象的把握，这就体现了几何画板

的函数图象功能，为进一步教学的开展做出了准备。有一就有二，函数图象创建出来之后，就有了发挥的空间。[y=x2-2x+1]”可以说是最简单的二次函数，我们从简单的入手再画几个二次函数的图象例如[y=-x2]，[y=x2-2x+1]，[y=ax2+bx+ca≠0]从简单到复杂，从特殊到一般，运用几何画板可以快速的得到它们的图象，这也体现了运用几何画板可以提高课堂效率，对于运用几何画板作图还可提高学生学习数学的积极性和创造性。

二、分析图象，研究性质

函数的性质是学习函数部分的关键所在，有了几何画板的帮助，我们就可以非常方便地绘制出函数图象，通过函数的图象来分析函数主要的性质。总结规律需要较多数量的个例分析，而几何画板恰好提供了一个“无限”的函数图象库。

我们以[y=x2-2x+1]为着手点，我在演示函数图象时，就已经绘制出了函数图象。

对于该函数的图象，我们可以发现，函数图象呈左右对称的形态，对称轴为直线[x=1]。函数与[x]轴有一个交点，与[y]轴有一个交点。函数的最小值为0，最低点为（1，0）。通过对函数图象的解读，我们发现了很多性质，那这些性质是[y=x2-2x+1]独有的，还是二次函数共有的性质？带着这种疑问，我们继续绘制图象。接下来我有选取了[y=x2+2x+1]、[y=-x2-3x+1]、[y=x2-2x+3]等多个函数，一一进行图象的绘制，并寻找图象的性质，最终发现这些函数既有共同点又有各自的特性。共同点是二次函数都具有相同的形状，即抛物线型，开口方向有上有下；每个抛物线都具有一条对称轴，对称轴对应了函数取最小值的那一点。不同点是函数图象与横轴的交点有较大差异，函数最多与[x]轴有两个交点，最少也可能没有交点。从图象上得出的性质都是直观的，同时也是非常重要的性质，如果仅从解析式上很难总结得出。既然函数图象已经绘制出来，再结合解析式，我们就可以将函数的各项性质完整地表达出来。在分析了图形中的性质之后，我又引导学生进行增减性的函数性质分析，同时将函数解析式与图象进行对应，收到了良好的效果。

数形结合的思想是研究数学的利器，通过几何画板生成函数图象的便利，学生在学习函数性质时不再是“被教”而是主动去探索，这对学生整个学习体系的建立、学习习惯的形成都是一个重要的契机。

三、函数变换，动态演示

二次函数具有三个参数，即二次项系数、一次项系数和常数项。如果已知了二次函数的三个参数，那么整个函数也就确定出来了。几何画板的一大优势就在于可以通过拖动已经形

成的图象从而改变参数。利用这一功能，我们可以更好地研究各项参数对函数的影响作用，一目了然。

我们知道二次函数的图象有两个重要的形状指标，即开口大小和开口方向，它的位置指标有四个方向，上下左右。开口方向我们可以从二次项系数的正负轻松判断出来，但是开口大小受什么因素影响呢？我们通过保持函数的水平、竖直位置不变，拖动曲线，使它的开口大小发生改变，观察原解析式的变化。我们可以在函数显示的窗口发现，随着开口的变大，二次项系数是逐渐变小的。再来看函数图象的位置影响因素，随着函数图象的拖动，我们发现函数的参数变化杂乱无序，很难分析特点。这是因为解析式的“看法”不对，我们换一种形式看即可。比如[y=x2-2x+1]。

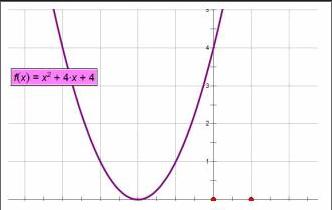
我们应当把它化成[y=x-12+0]，这样一来，当函数位置发生变化时，对应的“1”和“0”也发生着变化，并且变化的幅度是一致的，我们就摸清了函数位置的影响因素就是化成平方式之后的两个参数。通过我们的图像演示发现，函数在产生左右平移时，最大最小值不发生变化；在上下平移时，最大最小值发生改变。在学生理解时，可能会出现误区，比如说到平移，就认为是常数项的改变，这是比较笼统的。在竖直方向上的平移取决于常数项的变化，这是因为在y值上加减某一个数，就直接作用在了常数项上。但是对于左右平移，要作用在x上，这就体现了整个式子都要发生改变，但是不像上下平移那么直接，需要进行一步运算，如[y=x2-2x+1]向左平移3个单位，就是变成[y=x-1+32]，即[y=x2+4x+4]。

通过图象的变化，学生能够理解变化中的影响因素是主要目的。几何画板的应用让这一过程变得可视化，学生理解起来会更容易。没有万能的公式，在函数的变换中获取知识，才是“万能之道”。

四、观察最值，总结规律

函数方面的题目，出题点最多之处莫过于最值问题，同样我们在二次函数的教学中也把最值问题当做重点来讲解。二次函数的最值问题可不仅仅是图象上显示的“峰值”这么简单，而是要与取值范围、函数图象开口方向等来联系紧密。

从函数图象上进行分析，当没有约束条件时，开口向上的函数有最小值，无最大值；开口向下的函数有最大值，无最小值。最值的取得是在对称轴线上取到的值，最值为对称轴对应的[x]值代入函数所取得的[y]值。假设函数解析式为[y=ax2+bx+ca≠0]，那么对称轴就是[x=-b2a]相应的最值代入[x]值即可。但是求最值的问题往往没有这么简单，当函数有一个取值范围，而恰巧的是，在取值范围内还取不到对称轴所对应的[x]值。利用几何画板，我标亮了取值范围，图象的取值就像被“刀子”切割了一样，那么最值取多少就一目了然了。通过几组练习，学生逐渐掌握了这样的分析方法。当约束只能取到[-1≤x≤2]这样的条件时，对于一些开口向上的函数就可以取到了最大值，如上图所示。再如当函数图象是一个动态函数时，例如点A，B的坐标分为（1，4）和（4，4），抛物线[y=ax-m2+n]的顶点在线段AB上运动，与X轴交于C，D两点（C在D的左侧），点C的横坐标最小值为-3，问点D的横坐标最大值为？像这类题目如果仅用黑板分析，那么很多同学理解起來就比较困难，因为图象的动态比较抽象，如果这时我们能借助几何画板来演示这个动态过程，如图：

那么肯定会大大降低这个题目的理解难度，而且还可以提高学生学习数学的兴趣。

从研究最值的过程中，学生收获的不仅是一个结论，更重要的是解决问题的能力。在练习、考试中，学生还会面临其他的最值问题，甚至可能遇到没见过的函数，掌握了方法才是关键所在。

以上就是笔者在自身的教学实践中总结的几何画板应用实例，过程中难免有所疏漏，敬请各位同仁进行指正。几何画板的应用，能最大限度地调动学生思维的积极性和创造性，潜移默化地促使学生自主学习的教学工具，作为教师绝不应当丧失学生般的“学习精神”，对于这些先进的教学方法应当及时学习，及时掌握，与学生在不断的配合中逐步提升教学效果。

参考文献：

[1]牟丽华.几何画板优化初中数学教学的案例研究[D].重庆师范大学，2012.

[2]蔡亮亮.探索几何画板在初中数学教学中的运用[J].中学课程辅导：教学研究，2015，9（29）.

[3]张晓芬.巧用几何画板优化数学教学[J].江西教育：教学版，2015（17）：35-35.

[4]李铭.用几何画板解决二次函数的教学难点[J].中学教学参考，2010（5）：24-25.