关于正整数不含分部量2的有序分拆的几个组合双射

郭育红， 王汝军

(河西学院 数学与统计学院, 甘肃 张掖 734000)

关于正整数不含分部量2的有序分拆的几个组合双射

郭育红， 王汝军

(河西学院 数学与统计学院, 甘肃 张掖 734000)

利用正整数有序分拆的共轭分拆, 分别给出了偶数2k、奇数2k+1和正整数n的不含分部量2 的自反的有序分拆数的递推关系式的组合双射证明. 此外, 还给出了NAGI关于正整数n不含分部量 2的有序分拆数的一个恒等式的不同组合双射.

正整数的有序分拆;共轭分拆;自反的有序分拆;组合双射;关系式

Journal of Zhejiang University(Science Edition), 2017,44(3):261-265

0 引 言

1919年，MACMAHON[1]首次定义了正整数的有序分拆，即把正整数n表示成一些正整数的有序和,其中的每一项叫该分拆的分部量.例如, 4的有序分拆有4, 3+1,1+3, 2+2, 2+1+1,1+2+1,1+1+2,1+1+1+1，共8个. 也可以将相同的分部量写成幂,将有序分拆表示成向量的形式. 例如,上述4的8个有序分拆是: (4), (3,1), (1,3), (22), (12,2), (1,2,1), (2,12), (14). MACMAHON[1]给出了有序分拆的一些性质和表示图, 称为Zig-Zag graph, 类似于无序分拆的Ferres graph,即将有序分拆每个分部量ni依次用一行含有ni个的点来表示,但要求下一行的第1个点与上一行的最后一个点对齐.例如分拆(6,3,1,2,2)的Zig-Zag graph见图1.

利用有序分拆的Zig-Zag graph给出该分拆的共轭分拆,即将Zig-Zag graph从左向右按列来读. 则图 1按列读产生的有序分拆 (15, 2, 1, 3, 2, 1) 就是分拆 (6, 3, 1, 2, 2) 的共轭分拆, 它们互为共轭.

图1 Zig-Zag 图Fig.1 Zig-Zag graph

MUNAGI[2-3]给出了包括Zig-Zag graph在内的5种求有序分拆的共轭分拆方法,本文只介绍direc detection of conjugates(简称DD)法, 是一种比较宽泛直接的表示法, 即正整数的任意一个有序分拆通常有2种形式:

(1)C=(1a1,b1, 1a2,b2, 1a3,b3，…),a1>0,ai≥0,i>1;bi≥2,i≥1;

(2)E=(b1, 1a1,b2, 1a2,b3, 1a3, …),ai≥0,bi≥2.

这里将有序分拆C的共轭分拆记为C′,于是上述2种形式的有序分拆对应的共轭分拆分别为：

(3)C′=(a1+1, 1b1-2,a2+2, 1b2-2,a3+2，…);a1>0,ai≥0,i>1;bi≥2,i≥1;

(4)E′=(1b1-1,a1+2, 1b2-2,a2+2, …),ai≥0,bi≥2.

例如，(1,3,4,13,2,12,6)的共轭分拆是

(1+1,13-2,0+2,14-2,3+2,12-2,2+2,16-1)=

(2,1,2,12,5,4,15).

利用有序分拆的共轭可给出一些分拆恒等式的组合双射证明.

文献[4]讨论了正整数不含分部量2的有序分拆, 给出了一系列计数结果. 包括正整数不含分部量2的自反的有序分拆问题. 正整数自反的有序分拆的定义如下:

定义1[1]如果正整数n的一个有序分拆的分部量从左向右读和从右向左读相等, 则这个分拆叫自反的有序分拆.

例如, (1,3,2,5,2,3,1)就是17的一个自反的有序分拆.

本文将利用正整数有序分拆的共轭分拆给出文献 [4] 中涉及的关于正整数不含分部量2的自反的有序分拆的几个组合双射证明. 文献[2] 给出了定理1的递推关系证法, 下文将给出该定理的组合双射证明.

定理1[2]正整数n的分部量2在左端或右端最多出现一次有序分拆数等于正整数n+1不含分部量2的有序分拆数.

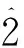
1 主要结果及证明

文献[4]给出了下面关于自反的有序分拆的结果.

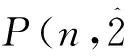
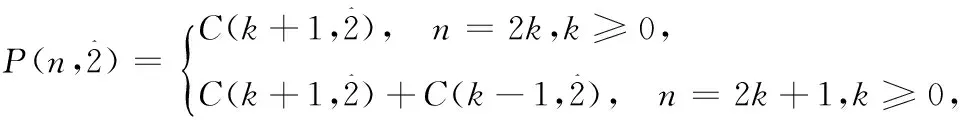
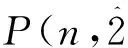
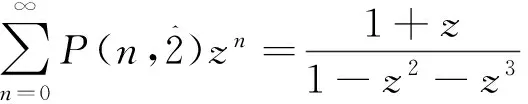
文献[4]给出了一种从中间分部量考虑累加的证法，本文则给出更直接的组合双射证明.

证明 (1) 当n=2k时,将n的不含分部量2的自反的有序分拆分成2种类型:

(A)分部量的个数为偶数;

(B)分部量的个数为奇数.

在(A)类中, 对于任何一个自反的有序分拆,由于分部量的个数是偶数, 于是以中间相同的2个分部量为准, 保留第1个, 删掉第2个及其右边的所有分部量, 然后在右端添上分部量1, 就得到k+1的右端分部量为1的不含分部量2的有序分拆. 反之亦然.

在(B)类中, 由于分拆的分部量个数是奇数, 这时, 显然中间的分部量为大于2的偶数2s,s>1. 将中间分部量除以2, 然后删掉右边的所有分部量, 得到一个右端分部量为s的分拆, 再用s+1代替s, 就得到k+1的右端分部量是大于1的不含分部量2的有序分拆. 反之亦然.故

(2)当n=2k+1时, 也将n的不含分部量2的自反的有序分拆分成2种类型来考查:

(C)中间分部量是3;

(D)中间分部量不是3.

在(C)类中, 将任何一个分拆的中间分部量3连同其右边的分部量都删掉, 就得到k-1的不含分部量2的有序分拆.

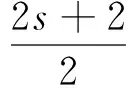
显然上述是一一对应的, 故有

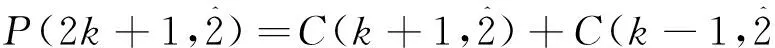
证毕.

由上述证明易得以下推论.

推论1 偶数2k,k>1的分部量的个数是偶数, 且不含分部量2的自反的有序分拆数等于k的不含分部量2的有序分拆数.

文献 [4]给出了关于正整数n的不含分部量2的有序分拆数的递推关系:

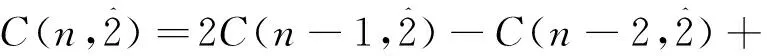
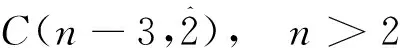
于是自然地有以下递推关系.

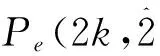
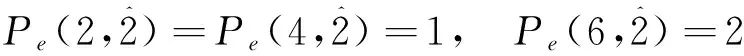
显然, 偶数的不含分部量2的自反的有序分拆数也满足以下递推关系式.

.

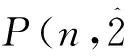
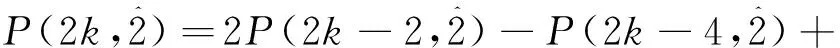
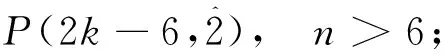
证明 将2k,2k-4的不含分部量2的自反的有序分拆分成以下3类:

(A)2k的首末两端分部量都是1的分拆;

(B)2k的首末两端分部量都是3的分拆;

(C)2k的首末两端分部量都是大于3的分拆, 以及2k-4的分拆.

对于(A)类中的任一个分拆, 删掉首末两端的分部量1, 得到2k-2的不含分部量2的自反的有序分拆. 反之亦然.

对于(B)类中的任一个分拆, 删掉首末两端的分部量3, 得到2k-6的不含分部量2的自反的有序分拆. 反之亦然.

对于(C)类中的2k的任一个分拆, 设首末两端的分部量d,d>3, 这时用d-1代替d, 于是得到2k-2的首末两端的分部量大于2的分拆, 即得到2k-2的首末两端的分部量不等于1的不含分部量2的自反的有序分拆; 对于2k-4任意一个不含分部量2的自反的有序分拆,给该分拆的首末两端分别添上分部量1, 就得到2k-2的首末两端的分部量等于1的分拆. 故(C)类中的分拆对应2k-2的所有不含分部量2的自反的有序分拆. 反之亦然.

综上,有

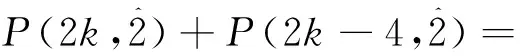
即

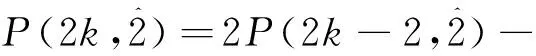
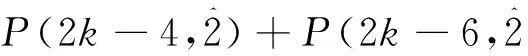
证毕.

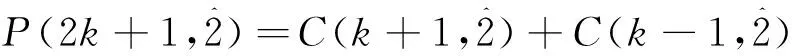
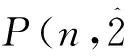
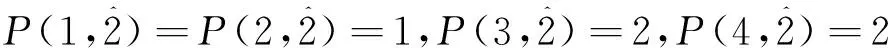
下面给出该关系式的组合双射证明.

证明 由于考查的是奇数的自反的有序分拆,故分部量的个数是奇数, 且中间分部量也是奇数.于是将2k+1的不含分部量2的自反的有序分拆分成2类:

(A)中间分部量不等于3;

(B)中间分部量等于3.

在(A)类中, 对于2k+1的任意一个自反的有序分拆, 设中间分部量是d, 于是用d-1代替d, 这时若d=1, 则得到2k的分部量是偶数的自反的有序分拆; 若d≠1, 则得到2k的分部量是奇数的自反的有序分拆. 反之, 对于2k的任何一个分部量的个数是偶数的自反的不含分部量2的有序分拆,在中间添加分部量+1, 可得2k+1的中间分部量是1的自反的不含分部量2的有序分拆; 对于2k的任何一个分部量的个数是奇数的自反的不含分部量2的有序分拆,此时中间分部量是偶数,给中间分部量+1,可得2k+1的中间分部量不等于1的奇数的自反的不含分部量2的有序分拆. 这样就得到了2k+1的所有不含分部量2的自反的有序分拆.

在(B)类中, 由于中间分部量是3,于是中间3个分部量组成分拆(s,3,s),这里s≠2.依据中间的分拆(s,3,s),将(B)类中的分拆又分为以下2种类型考虑:

(a)中间的分拆(s,3,s)中s>1;

(b)中间的分拆(s,3,s)中s=1.

对于(a)类中的任一个分拆, 求该分拆的共轭分拆, 仍得到分部量个数是奇数的自反的分拆, 这是因为若设正整数n的有序分拆的分部量个数为t, 则其共轭分拆的分部量个数为n-t+1. 且此时得到的共轭分拆的中间3个分部量组成的分拆必然是(2,1,2),于是删掉中间的分拆(2,1,2), 可得2k-4的分部量个数为偶数的自反的有序分拆, 然后再求该分拆的共轭, 可得2k-4的分部量个数为奇数的不含分部量2的自反的有序分拆.

反之, 对于2k-4的分部量个数为奇数的任一个不含分部量2的自反的有序分拆, 先求其共轭, 得到分部量是偶数的分拆, 再在中间添上分拆(2,1,2), 然后求所得到的2k+1的分拆的共轭分拆, 可得2k+1的中间分部量为3的自反的分拆.

于是, (a)类分拆对应2k-4的分部量个数为奇数且不含分部量2的自反的有序分拆.

在(b)类中, 直接删掉中间分拆(1,3,1), 则得到2k-4的分部量个数为偶数的不含分部量2的自反的有序分拆. 反之, 对于2k-4的分部量个数为偶数的不含分部量2的自反的有序分拆, 中间添上分拆(1,3,1)，可得2k+1的中间分拆是(1,3,1)的相应有序分拆.

综上, (B)类中的分拆对应2k-4的所有不含分部量2的自反的有序分拆.故有

证毕.

下面用例子说明上述组合双射.

例1 17的分拆(4,3,3,3,4),(1,1,4,1,3,1,4,1,1)与12的分拆(4,4,4), (1,1,4,4,1,1)之间的对应关系如下:

.

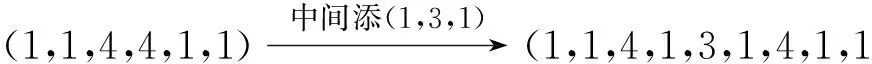
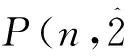
证明 将n的不含分部量2的自反的有序分拆分成2类:

(A)首末两端的分部量等于1;

(B)首末两端的分部量大于1, 包括只含一个分部量的情形.

对于(A)类中的任何一个n的不含分部量2的自反的有序分拆, 删掉首末两端的分部量1, 就得到n-2的不含分部量2的自反的有序分拆. 反之, 对于n-2的任何一个不含分部量2的自反的有序分拆, 在首末两端添上分部量1,则得到n的首末两端分部量是1的自反的不含分部量2的有序分拆.

对(B)类分拆, 又可分为2种类型考虑:

(a)n为偶数;

(b)n为奇数.

在(a)类中考虑以下2种情形:

情形1： 分部量的个数是奇数, 这时中间分部量是偶数, 由于不含分部量2, 故中间分部量为大于2的偶数, 于是将中间分部量-3, 得到n-3的首末两端分部量均大于1的相应分拆. 反之亦然.

情形2： 分部量的个数是偶数, 此时先求该分拆的共轭,再将得到的共轭分拆的中间3个分部量分别-1,可得n-3的首末两端分部量都为1的相应分拆. 反之亦然.

在(b)类中亦考虑2种情形:

情形1： 中间分部量为大于1的奇数, 这时将中间分部量-3, 得到n-3的首末两端分部量都大于1的相应分拆. 反之, 对于n-3的首末两端分部量都大于1的分拆, 当分部量的个数为偶数时, 中间添分部量3; 当分部量的个数为奇数时, 中间分部量+3, 可得n的中间分部量、首末两端分部量均大于1的相应分拆.

情形2： 中间分部量是1, 这时先求该分拆的共轭, 再将得到的共轭分拆的中间3个分部量分别-1, 就得到n-3的首末两端分部量都为1的相应分拆. 反之亦然. 特别地, 对于分拆(k,1,k), 对其共轭分拆(1k-1,3,1k-1)的中间3个分部量分别-1, 得到分拆(1k-2,3,1k-2),然后将中间的分部量2再分拆成1+1, 得到n-3的只含有分部量1的分拆.

反之,n-3只有分部量1的分拆对应n的分拆(k,1,k).

证毕.

下面用例子来说明上述证明中(B)类的对应关系.

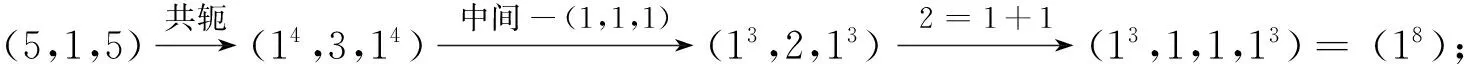
定理1的组合证法 将正整数n+1的不含分部量2的分拆分为以下4类:

(A)最右端的分部量等于1;

(B)最右端的分部量等于3;

(C)最右端的分部量等于5;

(D)最右端的分部量大于3,但不等于5.

对于(A)类中的分拆,将右端的分部量1删掉,就得到了n的不含分部量2的分拆. 反之亦然.

对于(B)类中的分拆, 将右端的分部量3减去1, 就得到n的最右端分部量是2的分拆.反之, 对于n的右端分部量是2的分拆, 给右端分部量+1就得到n+1的只出现1个分部量2在右端的分拆.

对于(C)类中的分拆,将右端的分部量5分拆成2+1+2, 然后删掉分部量1, 并将2个2分别放在去掉分部量5的分拆的首末两端, 得到n的首末两端分部量都为2的分拆. 反之亦然.

对于(D)类中的分拆, 将右端的分部量d分拆成2+t, 并分别将2和t-1放在去掉分部量d的分拆的左右两端, 得到n的仅左端是分部量2的分拆. 因为d>3,d≠5,故t-1≠2. 反之，n仅左端是分部量2的分拆, 将其左端的分部量与右端的分部量相加再+1后放在右端, 则得到n+1的右端分部量为大于3且不等于5的分拆.证毕.

[1]MACMAHONPA. Combinatory Analysis：Vol 1 [M]. Cambridge: Cambridge University Press,1915.

[2] MUNAGI A O. Primary classes of compositions of numbers [J]. Annales Mathematicae et Informaticae,2013,41:193-204.

[3] MUNAGI A O. Zig-Zag graphs and partitions identities of A.K. Agarwal [J]. Annals of Combinatorics,2015,19(3):557-566.

[4] CHINN P, HEUBACH S. Integer sequence related to compositions without 2’s [J]. Journal of Integer Sequences,2003(6): Article 03.2.3.

Several combinatorial bijections about compositions without 2’s of positive integers.

GUO Yuhong, WANG Rujun

(SchoolofMathematicsandStatistics,HexiUniversity,Zhangye734000,GansuProvince,China)

Using the conjugate of compositions, we present combinatorial bijective proofs of the recurrence relation of the self-inverse compositions without 2’s of even 2k, 2’s of odd 2k+1, and without 2’s of positive integern, respectively. In addition, we also obtain the combinatorial bijection of an identity which was obtained by MUNAGI relating to the number of the compositions without 2’s of positive integern. The methods used in this paper are different from the proofs of MUNAGI.

compositions of positive integer; the conjugate of compositions; the self-inverse compositions; combinatorial bijection; relation

2015-11-02.

国家自然科学基金资助项目(11461020).

郭育红(1970-)，ORCID：http://orcid.org/0000-0002-1403-2033，女，硕士，教授，主要从事组合数学研究，E-mail：gyh7001@163.com.

10.3785/j.issn.1008-9497.2017.03.002

O 157

A

1008-9497(2017)03-261-05