例谈高考试题中的转化与化归思想
辽宁省实验中学分校 毛洪
转化与化归的思想方法,就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化,进而得到解决的一种方法.一般总是将复杂的问题通过变换转化为简单的问题,将难解的问题通过变换转化为容易求解问题,将未解决的问题通过变换转化为已解决的问题.
转化与化归的原则有:熟悉化原则、简单化原则、直观化原则、正难则反原则.转化与化归的思想方法用在研究、解决数学问题时,可以将问题从一种状态转化到另一种状态,也就是转化到另一种情境,从而使问题得到解决,这种转化是解决问题的有效策略.
常见的转化方法有:(1)直接转化法:把原问题直接转化为基本定理、基本公式或基本图形问题;(2)换元法:运用“换元”把式子转化为有理式或使整式降幂等,把较复杂的函数、方程、不等式问题转化为易于解决的基本问题;(3)数形结合法:研究原问题中数量关系(解析式)与空间形式(图形)关系,通过互相变换获得转化途径;(4)等价转化法:把原问题转化为一个易于解决的等价命题,达到化归的目的;(5)构造法:“构造”一个合适的数学模型,把问题变为易于解决的问题;(6)坐标法:以坐标系为工具,用计算方法解决几何问题等.
本文仅以近些年的几道高考数学题为例,剖析其中的转化与化归思想.
一、函数、方程、不等式之间的转化与化归
例1(2014年北京卷)已知函数f(x)=xcosxsinx,x∈
(1)求证:f(x)≤0;
【解析】此处仅对第(2)问作出分析.
(2)解法 1(参变量分离):
解法2:(一端化零,分类讨论)
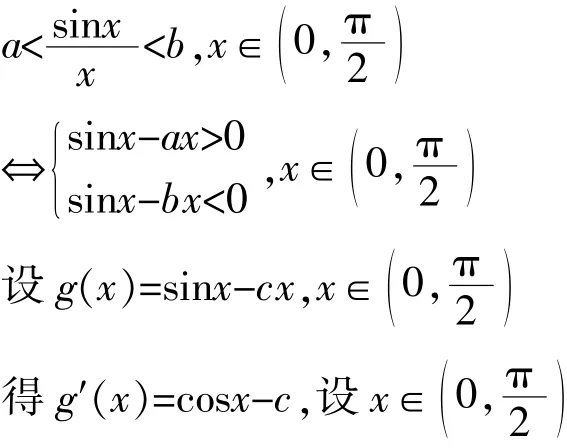
【说明】函数、方程和不等式就像“一胞三兄弟”,解决方程和不等式问题,需要函数的帮助,解决函数的问题需要方程和不等式的帮助.因此借助于函数、不等式和方程进行转化与化归可以将问题化繁为简,一般可将不等式问题转化为最值(值域)问题,从而求出参变量的范围.解法1和解法2都是将不等式问题转化为函数最值问题。学生在面对不等式恒成立问题时,首先就会想到参变量分离,求函数最值,解法1中g(0)不存在会导致学生仅利用高中知识体系无法求出b的最小值.是否能在高中教学中渗透洛比达法则,可因学生理解和学习的能力不同,因人而异.
解法2中如何对参数进行分类是学生运用分类讨论思想解题时的一大难点,引导学生关注端点函数值是否为零以及导数的变号零点是分类的关键.其中当0<c<1时,零点不可解出,为讨论增加了难度.
二、数量关系与空间图形之间的转化与化归
著名数学家华罗庚说过:“数缺形时少直观,形少数时难入微.”本题通过对不等式进行适当变形,从几何角度剖析,直观明了.
例1的解法3(几何意义法):
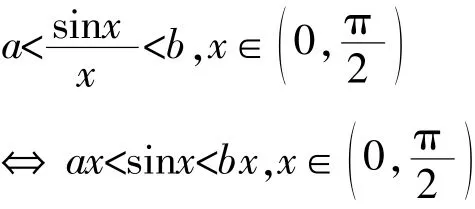
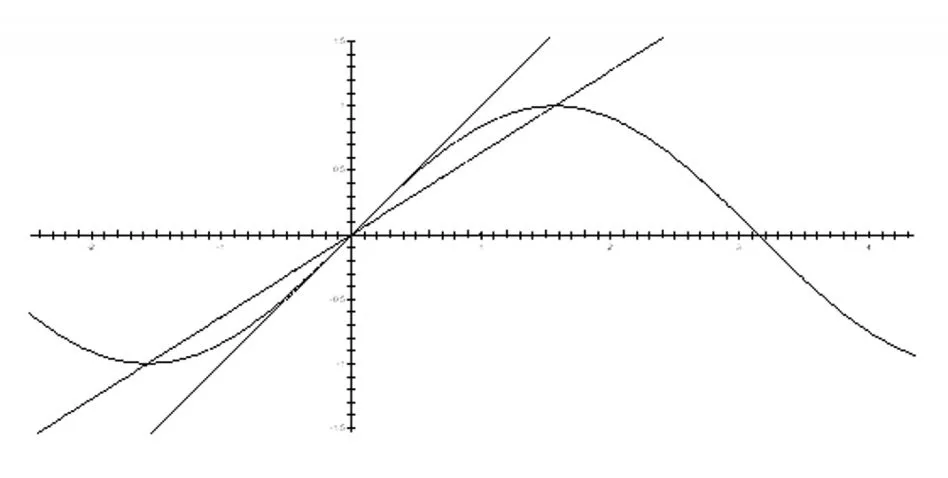
【说明】几何意义法十分直观清晰,体现了用数形结合思想解题.但笔者在实际教学中却发现,学生面对函数问题时,较少联想到它的几何意义,从而错失了一个如此简洁的解题思路.这还需要一线教师在教学时,经常挖掘题目的几何直观意义,并在教学中常常渗透数形结合思想.
无独有偶,从几何角度剖析高考试题,往往可以得出简洁清晰的解答方法.
例 2(2013年江苏卷)设函数f(x)=lnx-ax,g(x)=ex-ax,其中 a为实数.
(1)若 f(x)在(1,+∞)上是单调减函数,且 g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若 g(x)在(-1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
【解析】此处仅对第(2)问作出分析.
(2)若 g(x)在(-1,+∞)上是单调增函数,则g′(x)=ex-a≥0在(-1,+∞)上恒成立
当 0<x<e 时,h′(x)>0,h′(x)单调递增且连续不断,
当 x>e 时,h′(x)<0,h′(x)单调递减且连续不断,
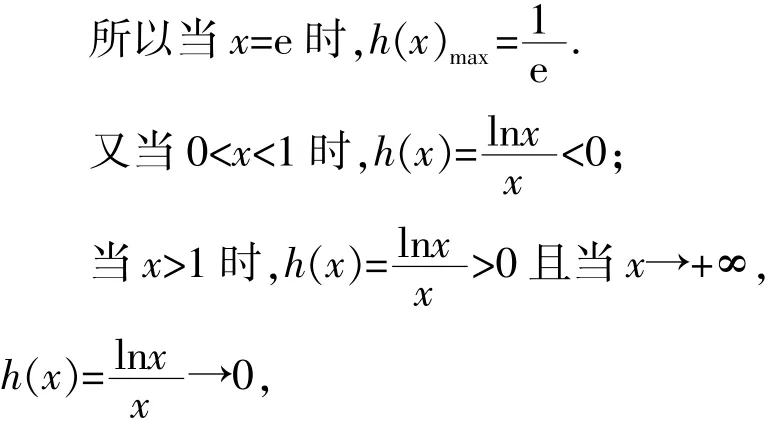
所以h(x)的图像以x轴正半轴为渐近线.
据此作出 h(x)的简图如下,则 f(x)的零点个数就是直线y=a与函数h(x)图像交点的个数.
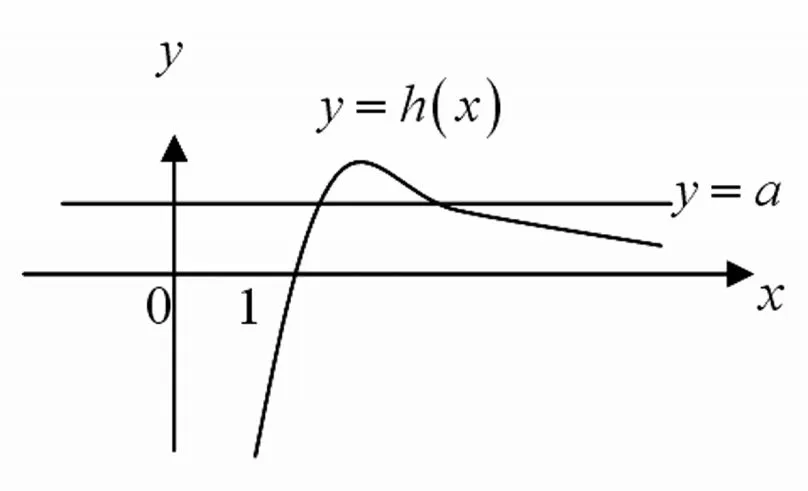
三、以换元为手段的转化与化归
例 3(2013 年陕西卷)已知函数 f(x)=ex,x∈R.
(Ⅰ)若直线y=kx+1与f(x)的反函数的图像相切,求实数k的值;
(Ⅱ)设 x>0,讨论曲线 y=f(x)与曲线 y=mx2(m>0)公共点的个数;
【解析】此处仅对第(Ⅲ)问作出分析.
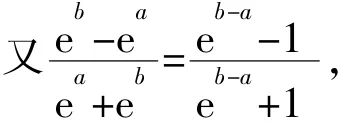

所以 h(x)在(0,+∞)上单调递增.
故有 h(x)>h(0)=0.
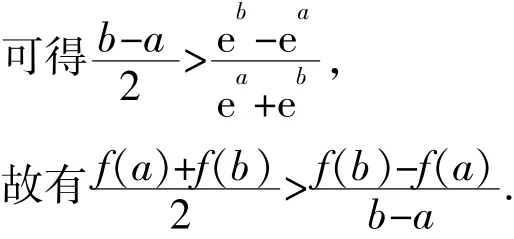
【说明】本题将二元不等式证明问题,通过适当变形,转化为以x=b-a为自变量的函数单调性问题.利用换元的手段将多元问题转化为单变量问题.
例 4(2014 年天津卷)设 f(x)=x-aex(a∈R),x∈R.已知函数 y=f(x)有两个零点 x1,x2,且 x1<x2.
(Ⅰ)求a的取值范围;
(Ⅲ)证明x1+x2随着a的减小而增大.
【解析】此处仅对第(Ⅲ)问作出分析.

于是 x1+x2为 t的函数 h(t)=(t>1),至此,通过换元,令t=已将二元问题转化成为一元问题.证明函数h(t)是增函数即可,过程略.
换元法可以将复杂多变量问题转化为单一变量的函数性质问题,再借助导数工具即可解决.
四、以构造为手段的转化与化归
本文例1还可以转化为定积分问题求解,具体如下:
解法4(定积分法)
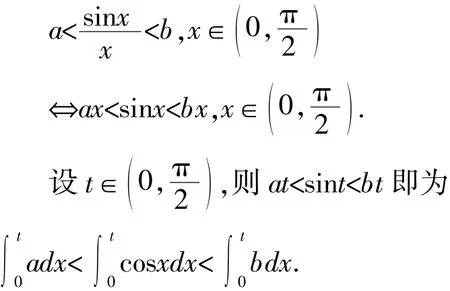
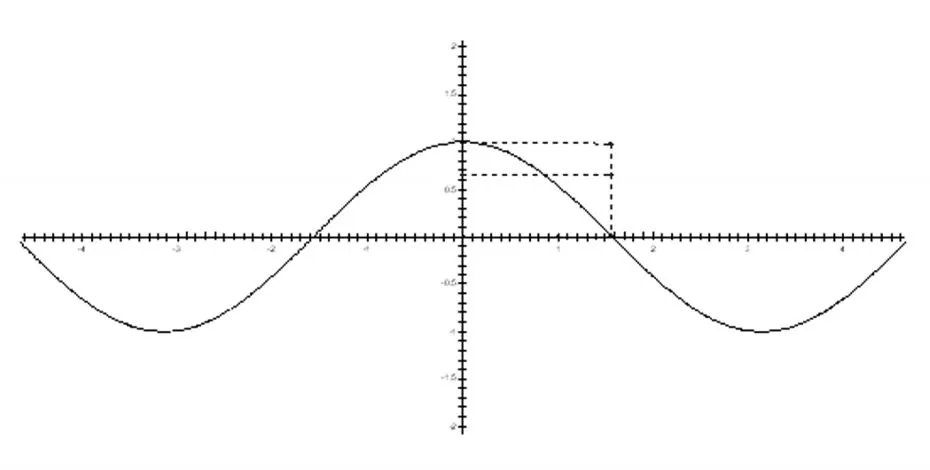
【说明】此种解法简洁新颖,其可行性依赖于题目区间端点的函数值恰好是不等式恒成立时的临界值.通过构造与原不等式等价的定积分,借助定积分的几何意义将函数间的大小关系转化为不同曲线围成图形面积间的大小关系,再转化为曲线和直线的位置关系是解题的核心,善于抓住图形中的临界位置和特殊点是解题的关键.
转化与化归思想在高考中占有十分重要的地位,数学问题的解决,离不开转化与化归,如未知向已知的转化、新知识向旧知识的转化、复杂问题向简单问题的转化,不同数学问题之间的互相转化、实际问题向数学问题的转化等.各种变换、具体解题方法都是转化的手段,转化的思想方法渗透到所有的数学教学内容和解题过程中.
在转化具体问题的教学中,我们应该引领学生学会把握转化与化归的指导思想:(1)把什么问题进行转化,即化归对象;(2)化归到何处去即化归目标;(3)如何进行化归,即化归方法.化归与转化思想是数学中解决问题的重要思想方法.

