一道2016年初中联赛几何证明题的多种证法
——高三复习课《三角恒等变换》教学实录与启示

四川师范大学数学与软件科学学院(610066) 罗燕 李昌勇

一道2016年初中联赛几何证明题的多种证法
——高三复习课《三角恒等变换》教学实录与启示

四川师范大学数学与软件科学学院(610066) 罗燕 李昌勇

2016年全国初中数学联赛决赛试题第13题是一道平面几何问题.

原题是：如图1,已知△ABC中AB=AC,点D是边AC上一动点,过D作DE//AB交BC于点E,点F为BD的中点.点O1、点O2分别为△CDE、△BDE的外接圆圆心.求证：

图1

一 参考答案及剖析

证明 (1)如图2,延长AF至G,使得FG=AF,则四边形ABGD为平行四边形;又由DE//AB知D,E,G三点共线,于是 DG=AB=AC;由条件知DE=DC,于是 △DO1E ∼= △DO1C;从而∠GDO1= ∠DEO1= ∠ACO1,又DO1=CO1,故 △DO1G ∼= △CO1A(SAS);于是O1G=O1A,而 AF=FG,所以O1F ⊥ AG,即 ∠AFO1=90°.

图2

评析 本题是将证明∠AFO1=90°转化为证明△AGO1为等腰三角形,从而由“三线合一”知O1F即是△AGO1的中线,也是△AGO1的高.在证明△AGO1为等腰三角形的过程中又将O1G、O1A放在两个三角形中,通过证明三角形全等得到O1G=O1A,这种思路对于学生而言更加容易想到.

(2)法一 因为⊙O1过D,E,⊙O2过D,E所以DE ⊥ O1O2;又DE//AB,所以AB ⊥ O1O2,注意到AF⊥O1F,FB⊥FO2.即△ABF与△O1O2F的对应边分别垂直,因此△ABF～△O1O2F,所以;又BF=FD,所以

法二 由△DO1G ∼=△CO1A知∠DO1G= ∠CO1A;又由∠DO1C= ∠DO1E知∠DO1A= ∠GO1E,注意到∠CDO1= ∠O1DE= ∠DEO1,于是∠DAO1= ∠DGO1,从而A,G,O1,D,四点共圆,于是∠FAO1= ∠GDO1=90°- ∠ACB,从而 ∠AO1F= ∠ACB;又 ∠DO2F=1/2∠DO2B=1/2·2(180°-∠DEB)= ∠DEC= ∠ACB,故 ∠AO1F= ∠DO2F;又 ∠O2FD=90°= ∠O1FA,故△O2FD～△O1FA,于是

评析 证明线段成比例,通常就是将这些线段放入某些三角形中,由三角形相似对应边成比例证得,只是所选的三角形不同,证明相似的难易程度就不同.法一利用问题(1)的结论,再找到一组垂直关系,证明相似就更容易,只是思维难度更大.法二这对三角形刚好包含这四条线段且刚好对应,运用了问题(1)的结论及过程中所得的全等三角形性质证相似,因此证明就显得更顺利成章了.这道题包含的几何知识非常丰富,因此解决这道题的方法也比较多,接下来介绍另外几种证法.

二 其他解法及剖析

(一)由三角形全等证垂直

图3

证明 (1)如图3,延长AF、DE交于G,显然四边形ABGD为平行四边形;又由DE//AB,F为BD中点,所 以 △ABF ∼= △GDF,则BG=AD,∠BGE= ∠BAD=180°-2∠ABC = 180°-2∠DEC = 180°-2∠BEG;所以 ∠GBE= ∠BEG,所以 EG=BG=AD;又DO1=EO1,∠DEO1= ∠EDO1= ∠O1DC,所以∠GEO1=180°-∠DEO1=180°-∠O1DC= ∠ADO1,所以 △ADO1∼= △GEO1,则AO1=GO1;又F 为AG中点,所以O1F ⊥ AF,即 ∠AFO1=90°.

评析 这种证法与参考答案的思路一致,只是所选的证明全等的三角形有所不同.所以将这种方法和参考答案归为“由三角形全等证垂直”.

(2)又 ∠DO1A= ∠GO1E,则 ∠AO1G= ∠DO1E=2∠C;又 O2为 △BDE 外接圆,则显然 ∠BED ＞ 90°,则∠BO2D=2∠DEC= ∠AO1G;又 BO2=DO2,AO1=O1G,所以△BO2D～△AO1G,故△O2FD～△O1FA,所以(F为BD,AG中点).

评析 这种证法的思想和参考答案的法二角度一致,只是证明△O2FD～△O1FA的方法不同,这种证法充分利用了问题一中△ADO1∼= △GEO1的结论及“整体”的思想,要比法二的证明更加容易.

(二)由三角形相似证垂直

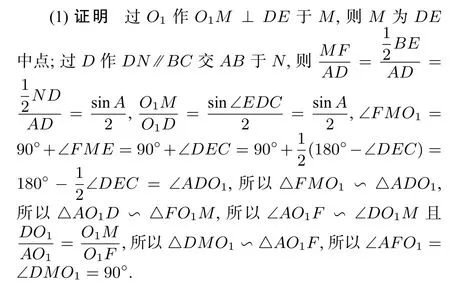
评析 这种证法是由相似三角形对应角相等证得的,直接构造一个直角三角形与∠AFO1所在的三角形相似是学生也比较容易想到的.

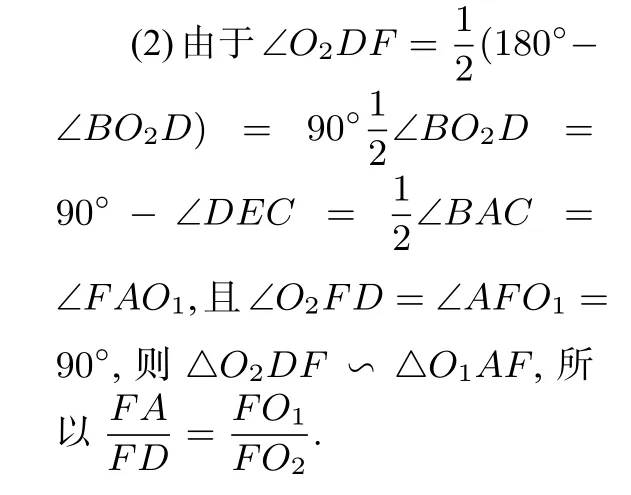
图4

评析 这种证法与参考答案的法二角度一样,但合理利用了题中条件所涉及的角度关系及问题一中的结论,使得证明△O2DF～△O1AF的难度降低了.

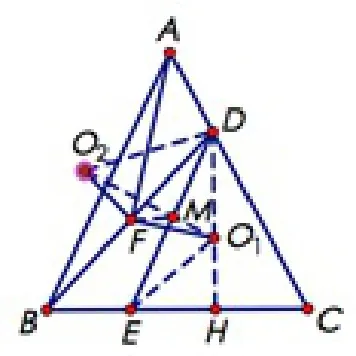
图5

(三)利用相似同时证明两个问

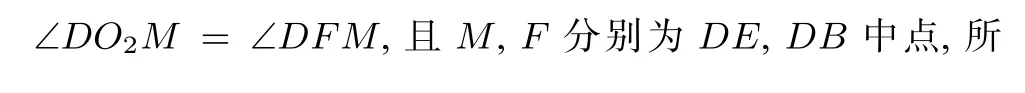
评析 此法通过证明△ABF～△O1O2F,由角的等量关系得到∠AFO1=90°,同时由这两个三角形的相似关系可以直接证得第二问,一举两得,只是考虑这组相似三角形的难度较方法(二)会更大一些.

(四)通过四点共圆证垂直

图6

评析 这种证法思维难度要大一些,需要有较强的几何观察力及丰富的几何知识,证明过程简单明了,但学生不容易想到这样的构造.

(2)因为

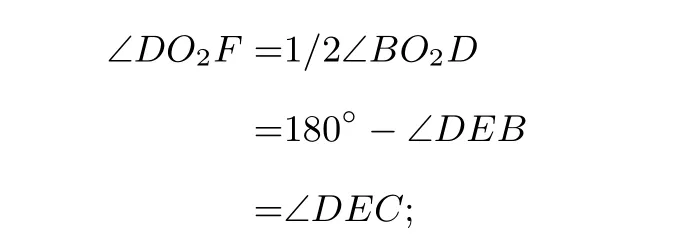
又 ∠O2FD= ∠DHE=90°,所以 △DO2F ～ △DEH;又△AO1F～△DO1M ～△DEH,所以△DO2F～△AO1F,所以

评析 同样是证明△DO2F～△AO1F,由于问题一的辅助线的添法使得证明△DO1M ～△DEH十分简单,同时由问题一中△ADO1～ △FMO1很容易证得△AO1F～△DO1M,从而得到△DO2F～△AO1F.

(五)从外心的角度证垂直

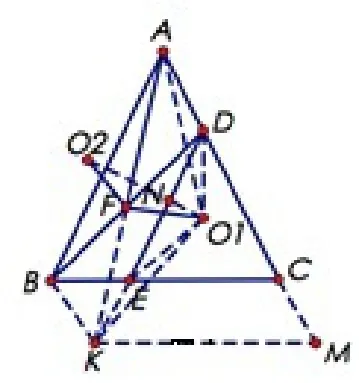
图7

证明 (1)作BK//AC交AF延长线于K,因为DE//AB,等腰△ABC,F为BD中点所以ABKD是平行四边形,所以BK=EK;作KM//BC交AC于M,CM=EK,AD=BK=CM,所以O1在AM 的中垂线上;因为O1为△DCE的外心,所以O1在EC的中垂线上,即在KM 的中垂线上,所以O1为△AKM外心;因为F为AK 的中点,所以O1F ⊥AK,即∠AFO1=90°.

评析 这种方法构造难度最大,首先想到利用中垂线证垂直是不容易的,其次外心是三角形三条中垂线的交点,那么如何构造一个三角形使得O1F是其一边上的中垂线,O1是它的外心就是最大的难点.同时在证明O1是△AKM的外心时,各种关系的转化也是较难的.

(2)作O1N ⊥ DE于N,因为∠O1FK= ∠O1NK=90°,所以O1,K,F,N 四点共圆,则 ∠NO1F= ∠NKF;同理O2,F,N,D四点共圆,则∠FO2N= ∠FDN,所以△O1FO2～△KFD,所以

评析 这种证法与参考答案中的法一思路一致,只是证明△O1FO2～△KFD方法不同,此法合理的利用了问题一的结论得图形中的“四点共圆”,思维难度较参考答案的法一要低一些.

竞赛中的几何题难度大,但题中所给的条件还是能够引发学生的一些思考,激发相关的知识结构网络.一道几何题的不同解法所呈现的思维方式不同,教学中应从学生的“就近发展区”展开对问题的讨论,由浅入深提高学生的思维层次.