ExplicitSolutionsofInitial-BoundaryValueProblemfor2×2LinearlyDegenerateSystems

WEI Zhen， YANG Yongfu

(Department of Mathematics, College of Sciences, Hohai University, Nanjing 210098, China)

ExplicitSolutionsofInitial-BoundaryValueProblemfor2×2LinearlyDegenerateSystems

WEI Zhen， YANG Yongfu

(DepartmentofMathematics,CollegeofSciences,HohaiUniversity,Nanjing210098,China)

Abstract： The explicit formula of the initial- boundary value problem for a class of 2×2 linearly degenerate quasilinear hyperbolic systems was presented. The existence and uniqueness of classical solutions for the initial- boundary value problem was presented by this method.

Keywords： quasilinear hyperbolic system; linearly degenerate system; initial- boundary value prblem; explicit solutions

CLCNumber： O 175.2Documentcode： A

It is well- known that for first order quasilinear hyperbolic systems, generally speaking, the classical solution exists only locally in time and the singularity may appear in a finite time[1- 2]. In some cases, however, the global existence of classical solutions can be obtained. For general quasilinear strictly hyperbolic systems with weakly linearly degenerate characteristic fields, the global existence and uniqueness ofC1solution to the Cauchy problem can be obtained, provided that the initial data is small inC1norm and decays at infinity[2- 4].

For the quasilinear strictly hyperbolic system of diagonal form, if the system is linearly degenerate, Yang[5]proved the existence and uniqueness of theC1classical solution to the mixed initial- boundary value problem on the domainD={(t,x)|t≥0,x≥0}. Moreover, Zhou and Yang[6]considered the mixed initial- boundary value problem for quasilinear hyperbolic systems with nonlinear boundary conditions on the domainD. Under the assumptions that the system is strictly hyperbolic and linearly degenerate or weakly linearly degenerate, the global existence and uniqueness ofC1solutions are obtained for small initial and boundary data.

Serre[7]used the characteristic method and obtained an explicit formula of solutions to the Cauchy problem for 2×2 diagonal systems. With the aid of a change of variables of Wagner’s type[8], Peng[9]deduced the explicit formula for the weak solutions of the Cauchy problem associated with tow kinds of 2×2 systems of conservation laws. Recently, Peng et al[10- 11]extened the similar results to rich systems.

As for the initial- boundary value problem, to our best knowledge, there are few results on the explicit representations for both classic and weak solutions. The goal of this paper is to provide explicit formula for the classic solutions of the initial- boundary value problem with two forward characteristic fields. To this end, we first decompose the initial- boundary value problem on the domainDinto two Cauchy problems and one Goursat problem. Then, we use a change of variables of Euler- Lagrange type to deduce the explicit solutions of the initial- boundary value problem. Moreover, the change of variables allows us to easily build the explicit expressions for theC1solution, so as to show the existence and uniqueness of theC1solutions. Finally, we give the explicit solutions of the initial- boundary value problem in different domains.

Now, we are concerned with the initial- boundary problem for quasilinear hyperbolic system whose characteristic fields are both linearly degenerate on the domain

D={(t,x)|t≥0,x≥0}.

It is well known that with a suitable choice of Riemann invariantswandzsuch a system can be written as

(1)

with initial data

t=0:w=w0(x),z=z0(x)x≥0,

(2)

where bothw0(x) andz0(x) areC1functions with boundedC1norms.

In what follows, we are going to discuss the initial- boundary value problem for system (1) with two forward characteristic fields.

To begin with, we suppose that

(3)

and on the boundary,

x=0:w=w1(t),z=z1(t)t≥0,

(4)

where bothw1(t) andz1(t) areC1functions with boundedC1norms and satisfy

(5)

Furthermore, we suppose that at the originO(0,0) the conditions ofC1compatibility are satisfied, namely,

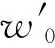
(6)

As a matter of fact, on the domainD, Liu and Zhou[12]essentially obtained the existence and uniqueness of theC1classical solution to the mixed initial- boundary value problem for system (1) with a forward characteristic and a backward characteristic. Moreover, they also established the uniformaprioriestimate for theC1norm of the solution (w,z). Similarly, it is easy to show that initial- boundary value problem (1)—(6) admits a unique globalC1solution with the uniformaprioriestimate. For the quasilinear hyperbolic system of diagonal form, if the system is linearly degenerate and strictly hyperbolic, Yang[5]proved the existence and uniqueness of theC1classical solution to the mixed initial- boundary value problem on the domainD. However, in the above two cases, the explicit expressions of theC1solution were not presented. We next construct a representation formula ofC1solution to the initial- boundary value problem (1)—(6). To this end, letΓ1:x=x1(t) be the characteristic satisfying

(7)

andΓ2:x=x2(t) be the characteristic satisfying

(8)

Consequently, the characteristic curvesΓ1andΓ2divide the domainDinto three parts denoted byD0,D1andD2, respectively, where

D0={(t,x)|t≥0,x≥x2(t)},D1={(t,x)|t≥0,x≤x1(t)},

D2={(t,x)|t≥0,x1(t)≤x≤x2(t)}.

(9)

Roughly, we are going to decompose the initial- boundary value problem on the domainDinto one Cauchy problem on the domainD0, one Cauchy problem on the domainD1, and one Goursat problem on the domainD2.

As in Ref.[9], on the domainDwe have

(10)

This allows us to make a change of Euler- Lagrange type (t,x)→(t′,y),y=Y(t,x) defined by

(11)

whereY0(x) is a strictly increasingC2function onx≥0. Similar to that in Ref.[9], on the domainD0we introduce

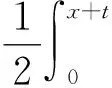
(12)

whereX0is the inverse function ofY0and it is easy to see thatXis also aC2continuous function with respect to their arguments. Thus, on the domainD0, we have

w(t,x)=w0(X0(Z(t,x)+t)),z(t,x)=z0(X0(Z(t,x)-t)),

(13)

hereZ(t,x) is the inverse function ofX(t,x). Obviously, on the domainD0, we haveZ≡Y.

So far, on the domainD0, we have established the explicit expressions for theC1solution (w,z). In what follows, we still need to construct the explict expressions for (w,z) on the rest domainsD1andD2.

We next solve the initial- boundary value problem (1)—(6) on the domainD1. Under the assumption (5), system (1) can be rewritten as

(14)

wherexis regarded as the original time variabletandtis looked on as the original space variablexin system (1).

We continue to solve the “Cauchy problem” (14) and (4) on the determinate domainD1. Similar to equation (10), on the domainD, we have

(15)

i.e.,

This also allows us to make a change of Euler- Lagrange type (x,t)→(x′,s),s=S(x,t) defined by

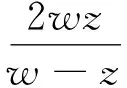
(16)

whereS0(t) is a strictly increasingC2function ont≥0. Likewise, on the domainD1we also introduce

(17)

whereT0is the inverse function ofS0and it is easy to see thatTis also aC2continuous function with respect to their arguments. Thus, on the domainD1, we have

w(t,x)=w1(T0(R(x,t)-x)),z(t,x)=z1(T0(R(x,t)+x)),

(18)

hereR(x,·) is the inverse function ofT(x,·). Obviously, on the domainD1, we also haveR≡S.

Finally, we consider the representation formula ofC1solution to the Goursat problem (1)—(6) on the domainD2. In this case, suppose that on the domainD2,

(19)

and

(20)

whereX0adnT0are defined by equation (12) and (17), respectively, and functionsYandSare to be determined later. Actually, in what follows, we are going to show that (Y,S) is the unique solution to the Cauchy problem for some ordinary differential equation(ODE) system.

It follows from equation (16) that

(21)

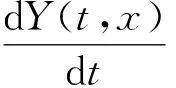
(22)

From the definition of the curveΓ2, it is easy to see that

(23)

where

is aC1function with respect to their arguments. Obviously, we deduce from equation (16) that

(24)

On the other hand, since the explicit expressions of the solutions have been obtained, we get on the curveΓ2,

(25)

As a result, on the curveΓ2, we have

(26)

Similarly, takingxas a parameter, we conclude that the system (21), (22) with boundary data equation (26) admits a unique global solutionY=Y(t,x),S=S(x,t) on the domainD2.

Thus, we have the following theorem.

Theorem1The initial- boundary value problem (1)—(6) admits a unique globalC1solution which is given explicitly by

(27)

whereX0andT0are the inverse functions ofY0andS0defined by equation (11) and (16), respectively.ZandRare the inverse functions ofXandTdefined by equation (12) and (17), respectively.Y=Y(t,x),S=S(x,t) is the unique solution to the Cauchy problem equation (21),(22) and (26).

Acknowledgements: The authors would like to thank Prof. Peng Yue- Jun’s suggestion for this problem and for helpful discussions. The authors are also grateful to Prof. Li Ta- Tsien and Prof. Zhou Yi for encouragement.

[1] LAX P D. Development of singularities of solutions of nonlinear hyperbolic partial differential equations [J].JournalofMathematicalPhysics, 1964,5(5) : 611- 613.

[2] LI T T. Global classical solutions for quasilinear hyperbolic systems [M]. Paris: Masson John Wiley & Sons, Ltd, Chichester, 1994.

[3] LI T T, ZHOU Y, KONG D X. Weak linear degeneracy and global classical solutions for general quasilinear hyperbolic systems [J].CommunicationsinPartialDifferentialEquations, 1994,19(7/8) : 1263- 1317.

[4] ZHOU Y. Global classical solutions to quasilinear hyperbolic systems with weak linear degeneracy [J].ChineseAnnalsofMathematicsSeries, 2004,25B(1) : 37- 56.

[5] YANG Y F. Mechanism of the formation of singularities for diagonal systems with linearly degenerate characteristic fields [J].CommunicationsonPureandAppliedAnalysis, 2009,8(2) : 757- 768.

[6] ZHOU Y, Yang Y F. Global classical solutions of mixed initial- boundary value problem for quasilinear hyperbolic systems [J].NonlinearAnalysis—TheoryMethods&Applications, 2010,73(6):1543- 1561.

[7] SERRE D. Intégrabilité dúne classe de système de lois de conservation [J].ForumMathematicum, 1992,4:607- 623.

[8] WAGNER D. Equivalence of the Euler and Lagrangian equations of gas dynamics for weak solutions [J].JournalofDifferentialEquations, 1987,68(1) :118- 136.

[9] PENG Y J. Explicit solutions for 2×2 linearly degenerate systems [J].AppliedMathematicsLetters, 1998,11(5):75- 78.

[10] PENG Y J. Euler- Lagrange change of variables in conservation laws [J].Nonlinearity, 2007,20(8) :1927- 1953.

[11] LI T T, PENG Y J, RUIZ J. Entropy solutions for linearly degenerate hyperbolic systems of rich type [J].JournaldeMathematiquesPuresetAppliquees, 2009,91(6) :553- 568.

[12] LIU J L, ZHOU Y. Initial- boundary value problem for the equation of timelike extremal surface in Minkowski space [J].JournalofMathematicalPhysics, 2008,49(4) : 043507.

2×2线性退化系统初边值问题的显式解

韦 真，杨永富

(河海大学 理学院，南京 210098)

给出了一类2×2线性退化拟线性双曲系统初边值问题解的显式公式，并证明初边值问题古典解的存在性和惟一性．

拟线性双曲系统； 线性退化系统； 初边值问题； 显式解

O175.2

A

ArticleID0427- 7104(2017)01- 0034- 06

Receiveddate2016- 02- 25

FoundationitemProject supported by NSFC(11571092)

Biography： WEI Zhen, female, graduate candidate; YANG Yongfu, male, associated professor, corresponding author, E- mail： yyang@hhu.edu.cn.