H0v空间上加权复合算子的超循环性

周 宁

H0v空间上加权复合算子的超循环性

周 宁

(天津大学 数学学院，天津 300350)

描述H0v空间中加权复合算子uCφ的超循环性，给出解析自映射φ是自同构或双曲非自同构时，加权复合算子uCφ在H0v空间上是超循环的充分条件，同时给出解析自映射φ是抛物非自同构时，加权复合算子uCφ在H0v空间上不是超循环的例子。

分式线性映射；加权复合算子；超循环

令D表示复平面上的开单位圆盘，H(D)表示D上解析函数全体，S(D)表示D上解析自映射全体。对于u∈H(D)，φ∈S(D)，定义加权复合算子uCφ如下：

(uCφf )(z) = u (z) f (φ(z))，f∈ H(D)，z∈ D

复合算子的研究是解析函数理论与算子理论相结合的产物[1-2]。

设v：D→(0，∞)是有界且连续的权函数，则Hv∞和H0v空间定义如下：

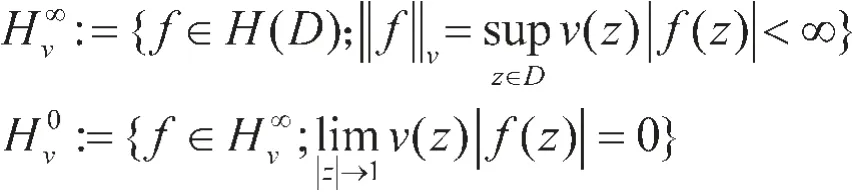
由文献[3]可知，在范数‖·‖v意义下，Hv∞和H0v空间是Banach空间，且多项式在H0v中稠密，因此H0v是可分的。

令X表示可分的无限维Banach空间，L(X)表示X上连续线性算子。T∈L(X)，若存在x∈X使得轨道orb(T，x)：=｛x，Tx，T2x，…}在X中稠密，则称T是超循环的。其中x称为T的超循环向量，HC(T)表示T的超循环向量全体构成的集合。

算子循环性的研究是线性动力系统中重要的内容之一[4-11]。文献[5]描述了复合算子在H0v空间上的超循环性。受其启发，本文主要研究加权复合算子在H0v空间上的超循环性。

1 预备知识

按不动点性质可将φ∈LFT(D)进行如下分类：

(1)若φ有唯一不动点，且在∂D上，则称φ是LFT(D)中抛物映射。

本文中会用到单位圆盘上解析自映射φ的迭代性质，为此需要应用Denjoy-Wolff定理。

定理1.1 (Denjoy-Wolff)若解析自映射φ：D→D在D内没有不动点，则存在α∈∂D使得φn的在D的紧子集上一致收敛于α。其中α称为φ的Denjoy-Wolff点。

在本文中为确保算子的超循环性，需要用到超循环准则。

定理1.2 (超循环准则)令X表示拓扑向量空间，T∈L(X)。我们说T满足超循环准则，如果存在一列递增的整数列(nk)，两个稠密子集D1，D2X和映射Snk：D2→X使得：Tnk(x)→0对任意x∈D1；Snk(x)→0对任意y∈D2；TnkSnk(y)→y对任意y ∈ D2。

上面的超循环准则是确保算子超循环性的充分条件。

在Hv∞和H0v空间中，v：D→(0，∞)是有界且连续的权函数，如果对任意z∈D满足v(z)=v(|z|)则称权函数为径向的。如果一个权既是径向的，同时关于|z|非增且，则称之为经典权。在本文中研究的权均为经典权。

2 H0v空间上加权复合算子的超循环性

引理2.1 若解析映射φ：D→D在D内没有不动点，如果αD且权是经典的，则在α点为0的多项式全体构成的集合Aα在Hv0中稠密。

证明：由文献[5]中Proposition3.3易得。

以下引理来自于文献[5]中Proposition3.4。

引理2.2 若v为经典权函数，解析映射φ：D→D在D内没有不动点。 如果α∈∂D是φ的Denjoy-Wolff点，则对任意多项式Ρ有。

定理2.3 如果加权复合算子uCφ在H0v上是超循环的，则解析自映射φ是单的，且在D中没有不动点，同时对任意z∈D，u(z)≠0。

证明：由于多项式在H0v和H(D)中均稠密，因此若uCφ在H0v上是超循环的，则在H(D)上也是超循环的，由文献[6]中命题1.1，我们得到这个结论。

由定理2.3可知，若解析自映射φ是椭圆映射（或斜驶的)，则加权复合算子uCφ在H0v上肯定不是超循环的。

定理2.4 若φ是双曲自同构或抛物自同构。 如果加权复合算子uCφ：H0v→H0v连续，且对z∈D有

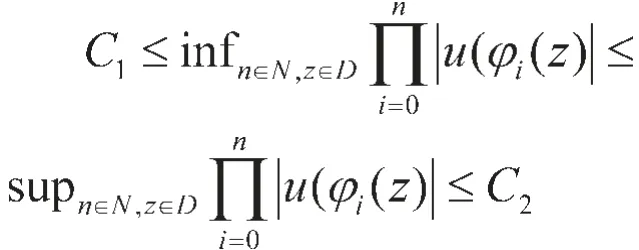
C1，C2为大于0的常数，则uCφ在H0v上是超循环的。

证明：由于φ是双曲自同构或抛物自同构，则有z0，z1∈∂D(可以有z0=z1的情形)使得φn(z)→z0对所有z∈D—{z1}和φn-1(z)→z1对所有z∈D—{z0}。根据引理2.1， 我们有Az0和Az1在H0v中稠密。

对任意f∈Az0，根据引理2.2，有

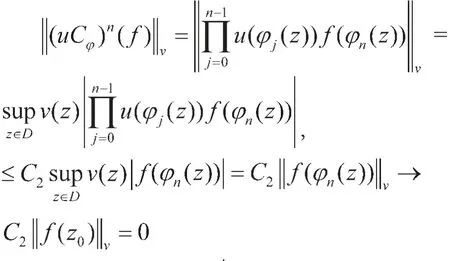
定 义Snf (z)=对z∈ D。同理，对于 f∈ Az1，‖Snf‖v→ 0，且 (uCφ)nSnf=f。因此，满足超循环准则，uCφ是超循环的。

例2.5 由定理2.4，易知φ∈Aut(D)且无内部不动点时，如果复合算子Cφ：H0v→H0v连续，则Cφ在H0v上是超循环的。

定理2.7 若φ是双曲非自同构的。如果加权复合算子uCφ：H0v→H0v连续，且对z∈D有

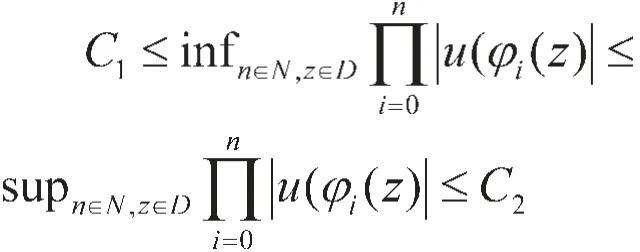
C1，C2为大于0的常数，则uCφ在H0v上是超循环的。

证明：该定理的证明类似于参考文献[2]中7.2节线性分式超循环定理(a)的证明。

由于φ是双曲非自同构，则有吸引点z0∈∂D使得φn(z)→z0，排斥点z1(D—在外，可能是∞)。根据引理2.1， 我们有Az0和Az1在H0v中稠密。首先，假设排斥固定点z1位于原点z0和确定的直线上，且和z0分别位于原点两侧。用△表示过z1点在z0处与D相切，且切线垂直于过原点、z0和z1的直线的开圆盘，则φ是△的共形自同构。对任意f ∈ Az0，同定理 2.4，‖(uCφ)n( f )‖v → 0，定义 Snf (z)=×对z∈D。同理，对于f∈ Az1，‖snf‖v→ 0，且 (uCφ)nsnf =f。此外，若 z1没有位于以上位置，则存在D的一个共形自同构γα固定z0且把z1映到以上位置。 因此，满足超循环准则，uCφ是超循环的。

定理2.8令v(z)=(1-|z|2)p，(0＜p＜1)，假设 φ ∈ LFT(D)

是抛物非自同构的，如果加权复合算子uCφ：Hv0→Hv0连 续， 且 对z∈D有supn∈N,z∈DC同时满足，当z→1时，u(z)不趋于0，则算子uCφ在H0v空间上不是超循环的。

证明：由于φ∈LFT(D)是抛物非自同构的，因此在∂D上有唯一不动点。不失一般性，不妨设其不动点为1。因此，由文献[2]，我们有

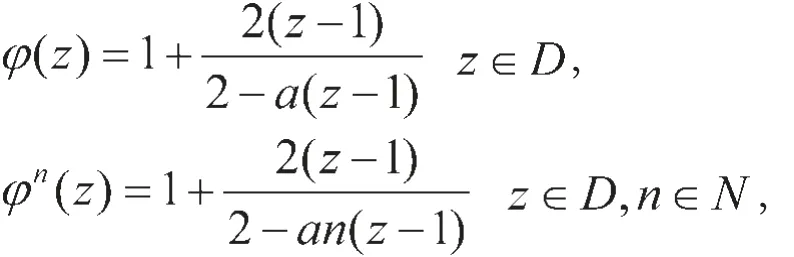
其中 a=φ"(1)，Rea＞0。

通过计算易得：

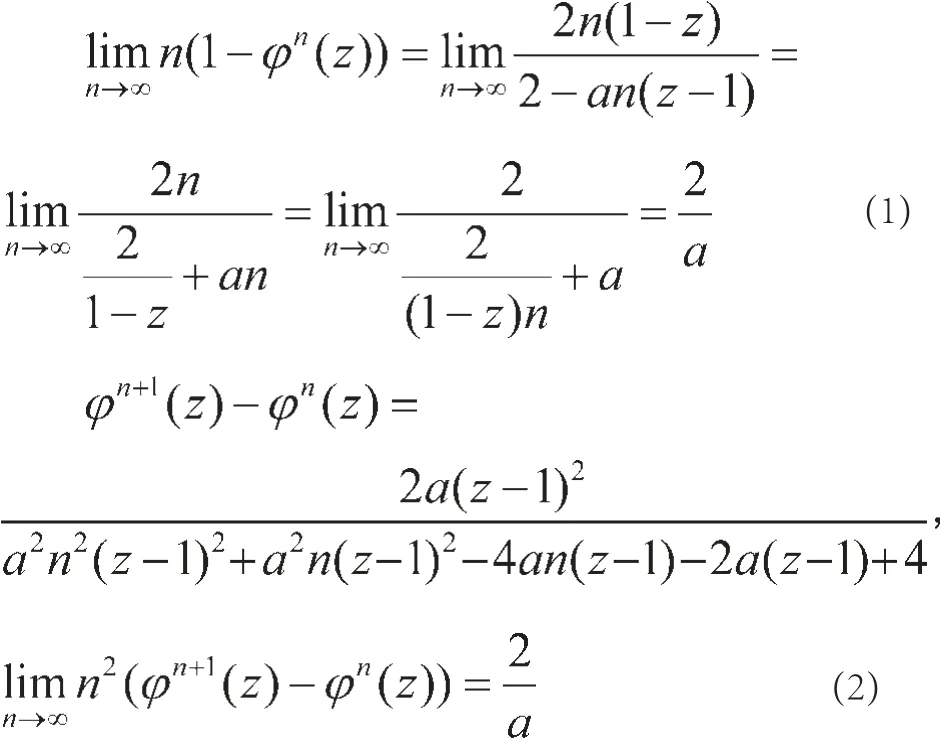
由于迹(φn(z))n非切逼近于固定点1，固定z∈D可知存在常数c ＞0使得对任意n。

1-|φn(z)|≥ c|1-φn(z)|，结合 (1)式和 (2)式可得

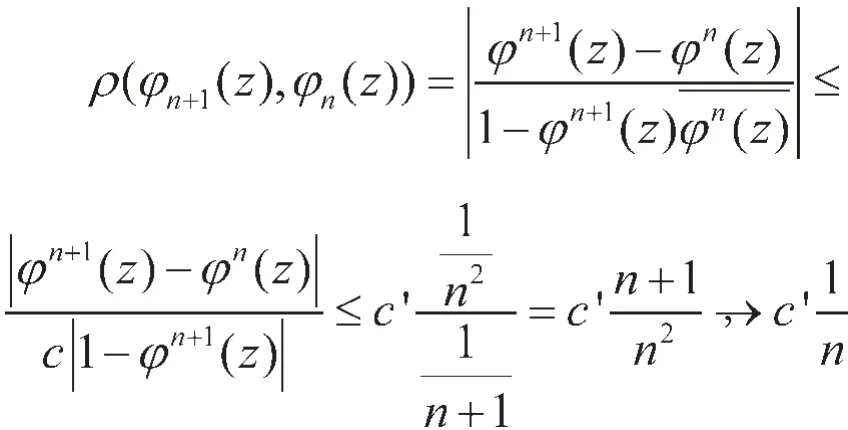
n→∞(c，c'为大于0的常数)。

在下面的证明中，为了方便，特用C泛指大于0的常数，与具体数值无关。

当v(z)=(1-|z|2)p(0＜p＜1)时，显然权v满足(L1)条件，由引理1.3得

设f∈H0v，

|(uCφ)n+1f(z)-u(φn(z))(uCφ)nf(z)|

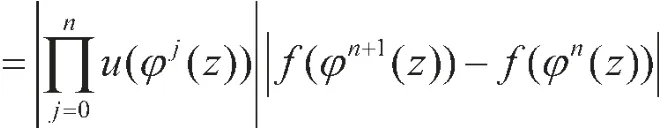
≤ C| f (φn+1(z))-f (φn(z))

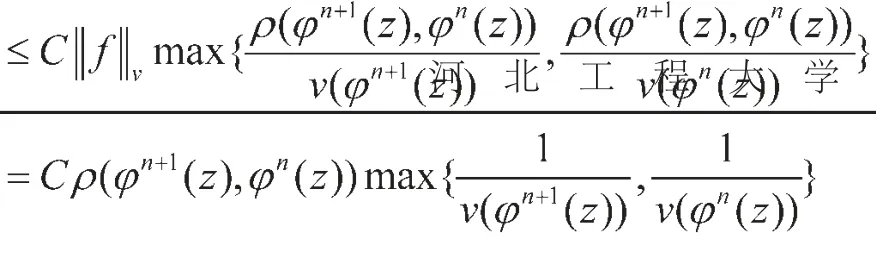
由(1)式，

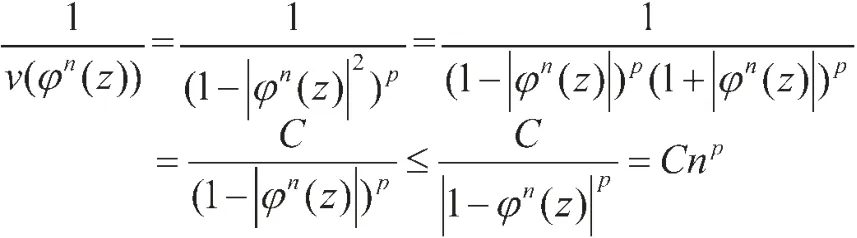
又因为迹(φn(z))n趋于固定点1，因此当n→∞时，u(φn(z))→u (1)且不趋于0，进而可得。

最后，假设f∈Hv0是uCφ的超循环向量，则对于g∈ Hv0存在数列 {nk}，当 k→∞时，‖(uCφ)nkf －g‖v→0，由于Hv0中范数收敛可以得到逐点收敛，因此对z∈D有

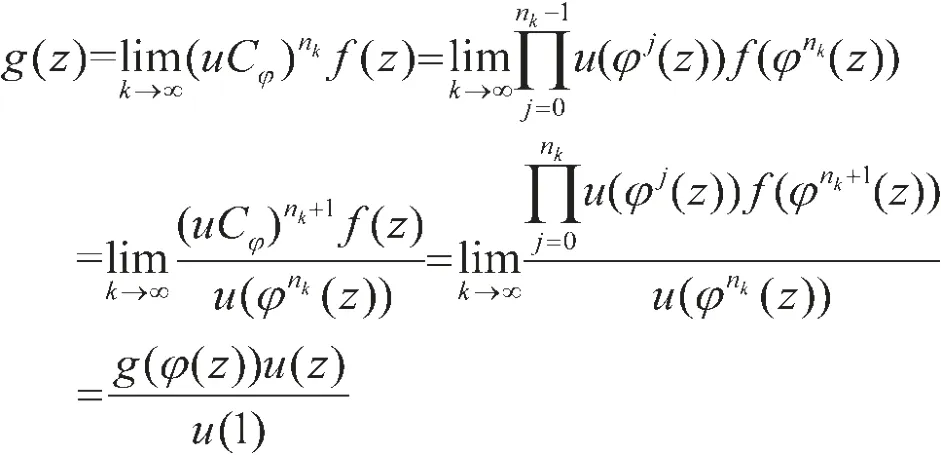
这与φ是非自同构矛盾，因此uCφ在H0v空间上不是超循环的。

3 结论

若 φ∈LFT(D)， 加 权 复 合 算 子 uCφ：H0v→Hv0(u∈H(D))连续。

1)当φ是椭圆映射(或斜驶的)时，算子uCφ在H0v空间上不是超循环的。

2)当φ是抛物自同构的或双曲的且对z∈D有

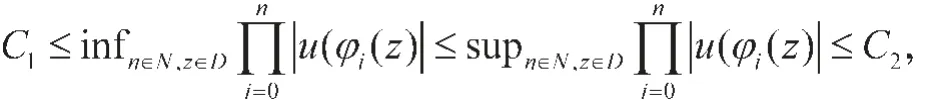
C1，C2为大于0的常数，则算子uCφ在H0v空间上是超循环的。

3)当φ是抛物非自同构的，令v(z)=(1-|z|2)p，(0＜p＜1)，且对 z∈D有同时满足当z→1时，u(z)不趋于0，则算子uCφ在H0v空间上不是超循环的。

[1]CCOWEN C C，MACCLUER B D.Composition operators on spaces of analytic functions[M].Boca Ralon：CRC Press，1995.

[2]SHAPIRO J H.Composition Operators and Classical Function Theory[M]. Berlin：Springer-Verlag，1993.

[3]LUSKY W.On the Structure of Hv0(D) and hv0(D)[J].Mathematische Nachrichten，1992，159(1)：279-289.

[4]ROLEWICZ S.On orbits of elements[J].Studia Mathematica，1969， 32(32)：17-22.

[5]ALEJRO M，ELKE W.Hypercyclic composition operators on-spaces[J].Mathematische Nachrichten，2013，286(1)：34-41.

[6]YOUSEFI B，REZAEI H.Hypercyclic property of weighted composition operators[J].Proceedings of the American Mathematical Society，2007，135(10)：3263-3271.

[7]ZHANG L，ZHOU Z H.Dynamics of composition operators on weighted Bergman spaces[J].Indagationes Mathematicae，2016，27(1)：406–418.

[8]LIANG Y X，ZHOU Z H.Hypercyclic behaviour of multiples of composition operators on the weighted Banach space[J].Bulletin of the Belgian Mathematical Society Simon Stevin，2014，21(3)：385-401.

[9]ZHANG L，ZHOU Z H.Hypercyclicity of weighted composition operators on a weighted Dirichlet space[J].Complex Variables & Elliptic Equations，2014，59(7)：1043-1051.

[10]BAYART F，ÉTIENNE Matheron.Dynamics of Linear Operators[M].Cambridge：Cambridge University Press，2009.

[11]BOURDON P S，SHAPIRO J H.Cyclic phenomena for composition operators[J].Memoirs of the American Mathematical Society，1997，125(596)：105.

[12]ELKE W.Differences of Composition Operators between Weighted Banach Spaces of Holomorphic Functions on the Unit Polydisk[J].Results in Mathematics，2008，51(3)：361-372.

Hypercyclicity of weighted composition operators on the H0vspace

ZHOU Ning
(School of Mathematics，Tianjin University，Tianjin 300350，China)

linear fractional transformation； weighted composition operators； hypercyclicity

O174

A

1673-9469（2017）03-0109-04

10.3969/j.issn.1673-9469.2017.03.024

2017-06-22

国家自然科学基金资助项目（11371276）

周宁（1992-），女，河北辛集人，硕士，从事多复变函数和算子理论方面的研究。

Absract：This paper characterizes the hypercyclicity of weighted composition operators on the Hv0space.The sufficient condition of hypercyclicity of weighted composition operators is presented， when φ is an automorphism or a hyperbolic non-automorphisms. The examples showing the fact that weighted composition operators uCφon the H0vspace are non-hypercyclic are also given， when φ is parabolic nonautomorphisms .