求解TSP问题的离散型差分进化算法∗
宁桂英 曹敦虔 周永权
(1.广西科技大学鹿山学院 柳州 545616)(2.广西民族大学理学院 南宁 530006)(3.广西民族大学信息科学与工程学院 南宁 530006)
求解TSP问题的离散型差分进化算法∗
宁桂英1曹敦虔2周永权3
(1.广西科技大学鹿山学院 柳州 545616)(2.广西民族大学理学院 南宁 530006)(3.广西民族大学信息科学与工程学院 南宁 530006)
针对旅行商(TSP)问题,提出了一种离散型差分进化算法,在该算法中,一方面,采用一种新的编码方法,把仅用于求解连续域上优化问题的差分进化算法推广到能用于求解离散TSP问题;另一方面,引入了2-OPT算子,将全局搜索与局部搜索有机地结合,通过对经典的TSP问题实例进行了测试,仿真结果表明,论文提出的算法具有较强的稳定性,是求解TSP问题的一种有效的方法。
差分进化;旅行商;启发式算法;适应度;2-OPT
1 引言
旅行商问题(traveling salesman problem,简称TSP)已被证明是一个典型的难以求解的NP-hand问题,它在生产线布局领域、库存配送领域及工程优化等领域有着广泛的应用,因此,寻找TSP问题的解具有重要的理论意义与实际应用价值。对TSP求解问题,目前的方法主要分为两大类:一类是精确算法(exact algorithms),如动态规划法、分支界限法、Dijkstra算法、Floyd算法、Bellman-Ford算法及改进的SPFA算法等[1]。这些算法的思想比较容易理解,理论上也能得到最优解,但在计算效率上不尽人意,难以解决大规模的问题;另一类是启发式算法(heuristic algorithms),如遗传算法(Genetic Algorithm,A)、模拟退火算法(Simulated Annealing,SA)、蚁群优化算法(Ant Colony Optimization,ACO)、禁忌搜索算法(Tabu Search,TS),最近领域搜索(Nearest Neighbor,NN)[2]、分层协同进化免疫算法(Hierarchical Co-evolution Immune Algorithm,HCIA)[3]、细菌觅食算法(Bacterial Foraging Algorithm)[4]及混合蛙跳算法(Shuffled Frog-Leaping Algorithm,SFLA)[5]等。这些算法虽不能保证在有限的时间内一定能得到问题的最优解,但通过大量的试验表明,这些启发式算法最终得到的最优解的误差能达到令人满意的程度。因此,启发式的群优化方法已成为目前人们求解TSP问题的一种有效方法。
差分进化算法(Differential Evolution,简称DE)是一种基于实数编码的,用于求解连续域上优化问题的智能优化算法,它是1995年由Storn和Price提出的,此后凭借其稳健性和强大的全局寻优能力在众多应用领域取得成功[6~7],如:图像处理、最优设计、参数识别等,尽管DE算法凭借其强有力的性能在连续优化问题上取得了巨大成功,但是在离散优化问题上应用较少,鉴于此,本文提出用离散差分进化算法(DDEA)求解TSP问题,该算法一方面结合TSP问题本身的特点,对DE算法提出了一种特殊的适用于求解离散问题的编码方法,另一方面,为了增强算法的局部搜索能力,加快收敛速度,在DE算法中引入具有较强局部搜索能力的2OPT算子[8],最后为了验证本文提出算法的性能,对14到200个经典的TSP问题进行了仿真,实验结果表明,本文提出的算法在解决中小规模的TSP问题中能够以较快的速度得到问题的最优解,验证了本文算法的有效性。
2 TSP问题概述
设某旅行商要拜访n个城市,规定每个城市必需且只能拜访一次,最后回到原出发城市,要求选择一条路径,使其沿着该路径行走的路程为所有路径中的最小值。
TSP模型可以表示为:设n个城市之间的距离矩阵为 D=(dij)n×n,其中dij代表城市i到城市 j的距离(i≠j),若i=j,定义 dij为一个足够大的实数M ,设 n(n>3)个城市分别标号为(1,2,…,n),一个TSP问题的可行解就是n个城市标号的环状排列,令π(n)为存放n个城市的任意排列的一维数组,则可行解的旅行总距离可表示为
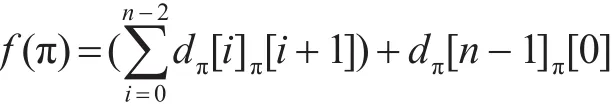
一个TSP问题的最优解是使 f(π)取得最小值的排列[9]。
3 求解TSP问题的离散型差分进化算法
3.1 标准DE算法步骤
3.1.1 变异操作
变异是差分进化算法用来产生新个体的一个关键步骤,变异操作主要通过下式进行:
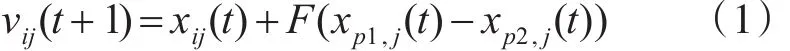
其中:xp1,xp2为任意选择的两个个体,p1,p2为[1,M]中任意选取的互不相等的随机整数,F为变异因子,i=1,2,…,M.j=1,2,…,n。
3.1.2 交叉操作
DE算法的交叉操作是将变异后的新个体与当前个体混合,然后按照以下规则选择哪个个体将进入下一代,交叉操作通常按下式进行:
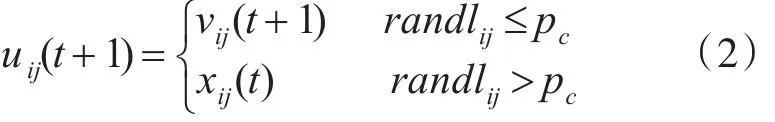
其中 pc为交叉因子,通常 pc取(0,1]之间的实数,randlij为[0,1]间随机数。
3.1.3 选择操作
为保证新生成的个体Ui是否进入下一代中,DE算法在进行交叉操作后,需要将新生成个体的适应度与当前种群中个体Xi的适应度进行比较。如果Ui的适应度优于 Xi,则选择Ui进入下一代;否则,直接让旧个体Xi进入下一代,具体操作为
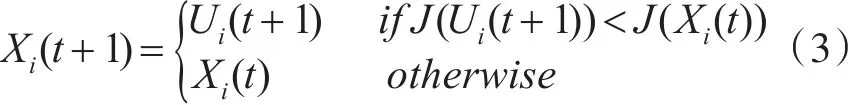
3.2 编码设计
变异操作是DE算法的主要操作,但这种操作是基于实数域上的四则运算,因此适用于连续域上的优化问题,而对于离散域上的组合优化问题的解是自然数的情况已不能满足要求。为了既保留DE算法变异算子的功能,又能解决离散域上的优化问题,本文提出一种特殊的编码方式。对包含n个城市的一个TSP问题,一个可行的编码是1到n上的随机整数构成的一个序列,如:序列(3,2,4,1,5)表示编号为3的城市在1号位置,编号为2的城市在2号位置,编号为4的城市在3号位置,编号为1的城市在4号位置,编号为5的城市在5号位置。通过DE变异算子之后,整数的运算不再满足封闭性,但是实数是有大小之分的,因此,可通过对变异后的实数按由小到大排序后再找出原来的数在新序中的位置这一方法来解决离散域上的优化问题。下面给出这一编码的定义。
定义1:设 Xi(t)=(xi1(t),xi2(t),…,xin(t))为DE算法第t代的一个基本个体,X'i(t)=(xi1'(t),xi2'(t),…,(t))为 Xi(t)按由小到大排序后的新个体,若xij(t)↔x'im(t),则称个体分量xij(t)经变异后对应分量为m。
如基本个体(-2.3,4.1,3.2,-1.5,2.4),升序排列后的个体为(-2.3,-1.5,2.4,3.2,4.1),对应的编码为(1,5,4,2,3)。
据定义1,通过DE算法的变异算子之后的任何个体均有一组对应的整数编码与之对应,因此,通过这种编码方法可以解决离散域上的TSP问题。
3.3 局部路径优化设计
尽管已有大量实验证明DE算法具有较强的稳定性和全局搜索能力,但与其它优化算法一样,标准DE算法也会存在收敛速度慢,易陷入局部极优等不足。因此,在求解TSP这一NP-hard问题时,考虑引入具有全局搜索能力的优化策略。已有文献表明,求解TSP问题的算法分为两大类型:一种是局部启发式搜索算法;一种是独立于问题的经典优化算法。常见的局部启发式优化算法有2-OPT,3-OPT和Lin-Kernighan(LK)等[8,10]。实验证明,在这些算法中,用2-OPT算子优化路径对求解TSP问题的局部最优解非常有效。但仅靠2-OPT算子本身的特性也会使问题陷于局部最优,因此,本文考虑首次将将具有较强全局搜索能力的DE智能算法与具有局部优化能力的2-OPT算子相结合,在进化前期用具有较强搜索能力的DE算法进行全面搜索,以增强群体的多样性,到后期对得到的路径再用2-OPT算子进行局部优化,以提高收敛速度和精度。
3.4 Complete 2-Opt(C2Opt)算子
在本文的算法中,先用DE算法对群体进行优化后,再对所有构成路径用C2OPT算子进行局部优化。
设ck为城市所在顶点,d(ci,cj)表示任意两个城市i与 j之间的距离,C2OPT算子的具体步骤如下[8]:
Step 1:选 取 一 条 路 径 c={c1,…,ci,ci+1,…,cj,cj+1,…,cn-1},并令 i=j=0 ;
Step 2:任选一条边,记为No.1:(ci,ci+1),其中i<n;
Step 3:任选另一条边,记为No.2:(cj,cj+1),其中i<n;
Step 4:如 果 |j-(i+1)| ≥2 且 d(ci,cj)+d(ci+1,cj+1)< d(ci,ci+1)+d(cj,cj+1),则用 2-Opt算子删 除 边 (ci,ci+1) 与 (cj,cj+1) ,并 连 接 边 (ci,cj) 和(ci+1,cj+1)且 ci+1与 cj的指向相反;
Step 5:再以cj作为No.2边下一个开始的城市,并令 j=j+1,重复Step 3~Step 4,直到 j=n-1,如果 j=n-1,令 j+1=0;
Step 6:以ci作为No.1边下一个开始的城市,并 i=i+1令,重复Step 2~ Step 5,直到 i=n-1,如果i=n-1,令i+1=0;
Step 7:重复Step 2~Step 6直到 N 次,使 N 足够大,直到所选取的路径无交叉边出现时终止。
图1和图2给出了使用C2OPT算子前和使用C2OPT算子后的示意图。
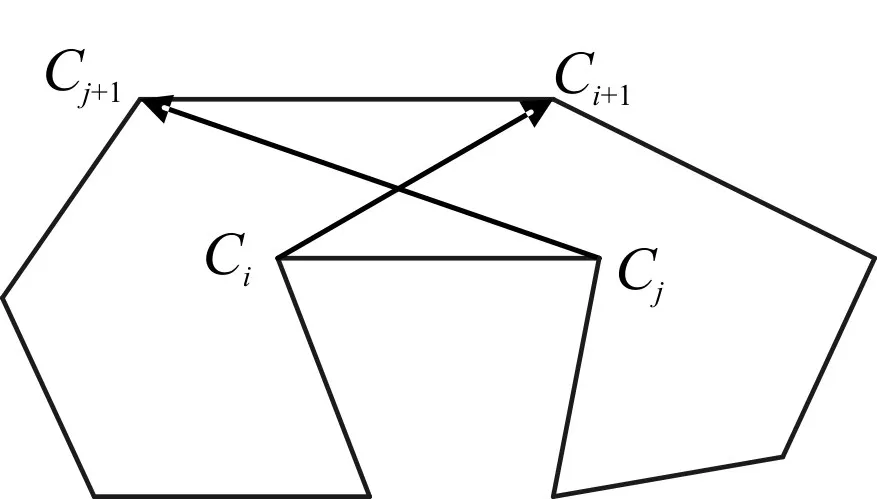
图1 使用C2OPT算子前

图2 使用C2OPT算子后
3.5 适应度函数选取
本文适应度函数取优化后对应路径长度的最小值。
3.6 参数设计
变异和交叉操作是DE算法的主要操作,而变异因子和交叉因子选取的好坏直接影响算法的性能,到目前为止,还没有一种选取方式能适合解决所有问题,据现有文献给出的范围,本文给出了变异算子F和交叉算子CR的最佳取值。以14个城市的TSP问题为例,此问题的已知的最优路径和为30.8785。

表1 不同参数运行结果
表1中给出了参数不同取值后运行10次所得平均结果。从表中可看出,求解TSP问题时,变异算子F和交叉算子CR的取值的不同对结果的影响很大,当F=0.5,CR=0.2时优化效果最好,从运行10次的平均值来看,此时的结果与最优值相当。因此,在本文算法中设置F=0.5,CR=0.2。
3.7 求解TSP问题的离散型DE算法具体步骤:
Step 1.初始化。随机生成1~n上的一个自然数序列,构成一个个体,依次生成m个初始种群,设置最大进化代数T,变异算子F和交叉算子CR;
Step 2.计算各个体的适应度;
Step 3.利用式(1)进行变异操作;
Step 4.对变异后的算子利用式定义1方法编码;
Step 5.利用式(2)进行交叉操作;
Step 6.对交叉后的个体利用2opt算子进行局部优化,生成新个体;
Step 7.选择操作;
Step 8.判断是否达到迭代要求,若是,停止,并输出路径和的最优结果,若否,则转Step 3。
4 算法性能分析
对本文提出的算法,在线性能定义如下:
定义2:设 f(t)为第t代群体的平均适应度,T为进化代数,则在同样的环境下,称为算法的在线性能。
在线性能表示算法在直到当前为止的时间内得到的所有性能的平均值,反映了算法的动态性能,图3给出了本文算法的在线性能曲线。
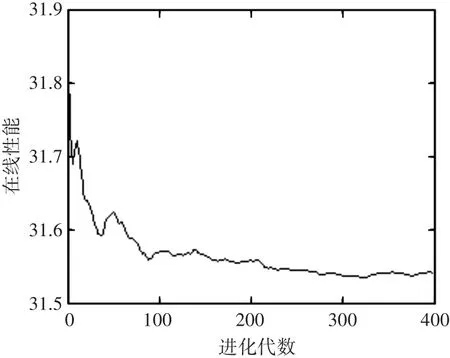
图3 在线性能曲线图
从图3可以看出,本文提出的算法具有较强的稳定性。
5 算例测试
由于Oliver30和Eil51经常被用来测试各种算法的测试实例,因此本文首先测试了Burma14,坐标为(16.47,96.10),(16.47,94.44),(20.09,92.54),(22.39,93.37),(25.23,97.24),(22,96.05),(20.47,97.02),(17.20,96.29),(16.30,97.38),(14.05,98.12),(16.53,97.38),(21.52,95.59),(19.41,97.13),(20.09,94.55)及Oliver30和Eil51的TSP问题,表2给出了本文算法的测试结果,并与文献[12]DGSO算法和文献[13]的SADPSO算法及文献[14]的ACO算法的结果进行了比较,从测试结果可以看出,四种算法对Burma14都能找到最优解,而对于Oliver30问题,本文算法进化200代就找到最优解,而且进化代数远比SADPSO少,收敛速度快,对Eil51问题,虽然与目前已知最优解有些差值,差值为1.3,但与文献相比都有所改进,说明本文算法的有效性。

表2 本文算法与相关文献结果比较
图4~图7分别给出了Oliver30和Eil51问题的最优路径图和进化曲线图。
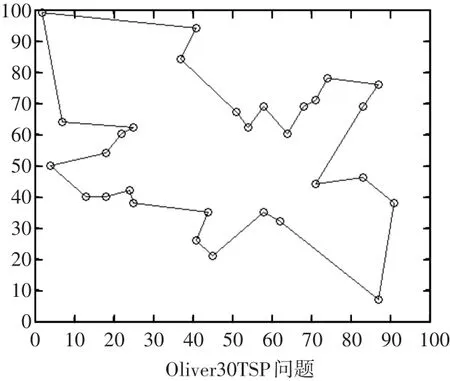
图4 本文算法优化Oliver30算例的路径图
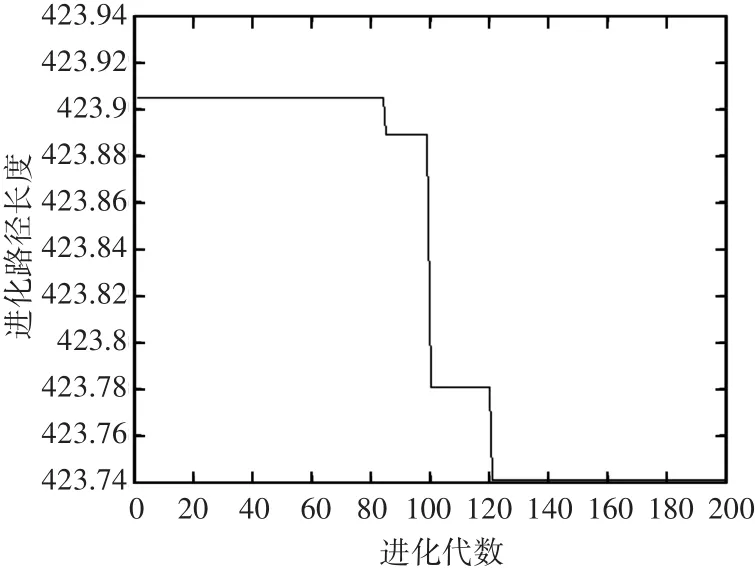
图5 本文算法优化Oliver30算例的进化曲线图
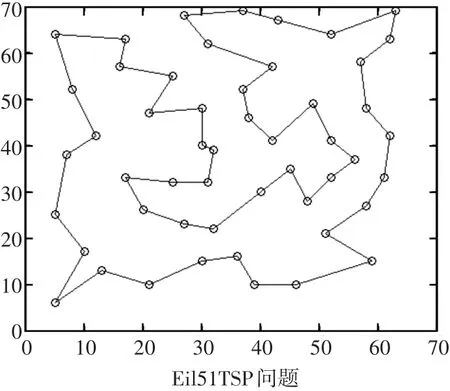
图6 本文算法优化Eil51算例的路径图
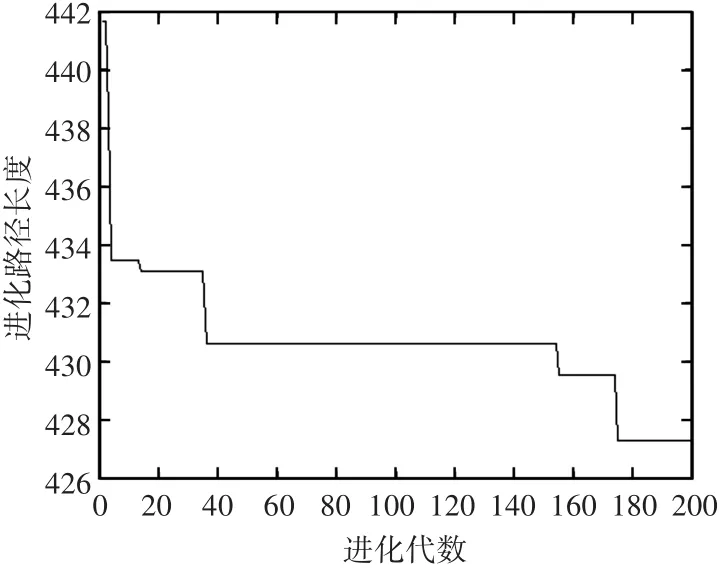
图7 本文算法优化Eil51算例的进化曲线图
为进一步验证该算法的有效性,本文选自城市数量为 48~200 的 Att48、kroa100、bier127、pr144、kroa200几个经典TSP问题进行了测试,这些测试实例选自国际通用的TSP标准库TSPLIB[15]。TSPLIB是一个开放的网络资源,其中收集了各种规模的TSP实例,并提供了所有实例的最优解作参考。为降低误差,本文与所给文献的参数设置基本保持一致,本文对每个算例运行10次,取其最优解,最差解和平均解作比较,并给出了本文算法所得结果的偏差率。最大进化代数为200,变异因子F=0.5,交叉因子CR=0.2,所得结果如表3所示。
从表3可以看出,对att48问题,本文算法每次都能找到问题的最优解,偏差为0,对Kroa100问题,虽然比标准库多出1,但是比文献[16]的改进的演化算法和文献[18]的离散型细菌觅食算法及文献[22]的多角色蚁群算法求解的结果好,而且进化代数少,耗时短,对bier127和kroa200问题,本文进化200代得到的最优结果较文献[20]的ACO&&SS算法进化2000代的效果好,而且也明显优于文献[21~22],充分显示本文算法的优越性,对pr144问题,找到的最优解比标准库给出的少2,从整个计算结果来看,本文算法计算偏差率都很低,说明该算法具有很强的稳定性和鲁棒性,能有效解决中小规模的TSP问题。
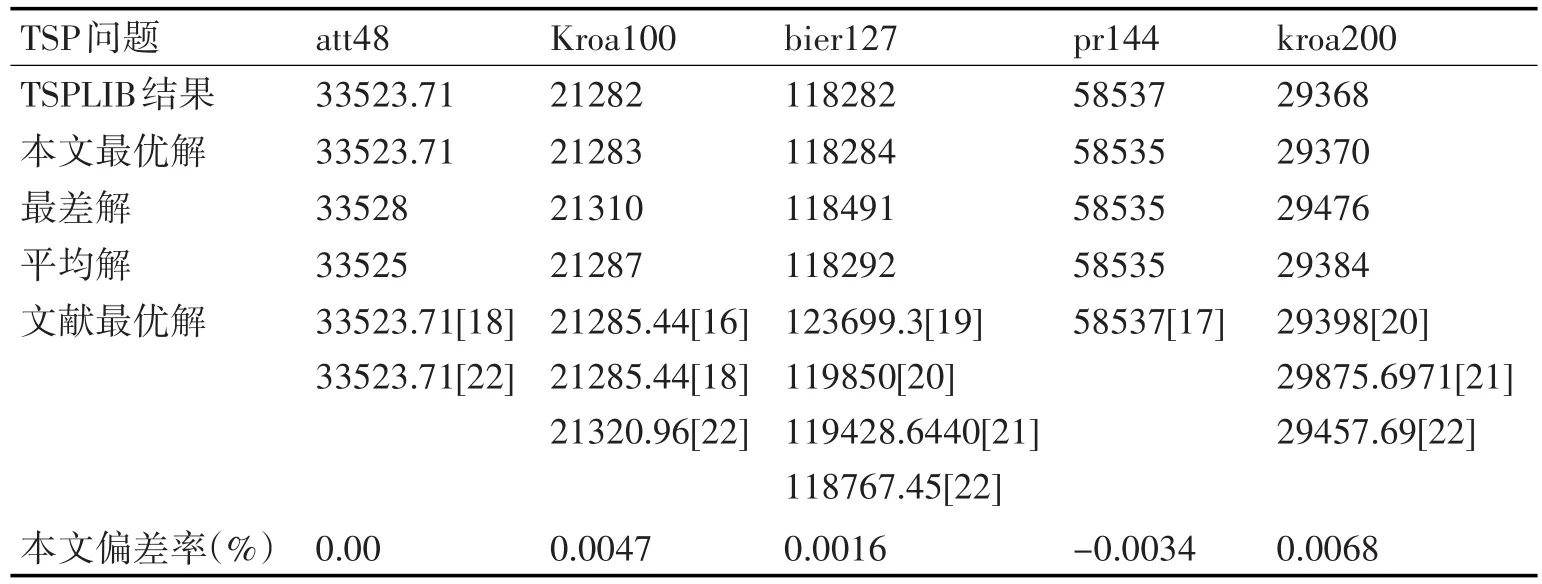
表3 本文算法计算结果与文献结果对比
偏差率是体现计算结果与最优解的偏离程度,偏差率越小,表明算法越稳定。本文中提到的偏差率计算公式为
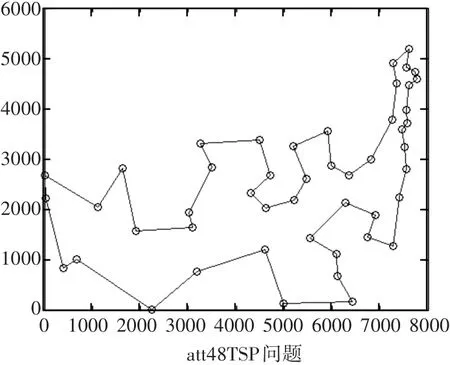
图8 本文算法优化Att48算例的路径图

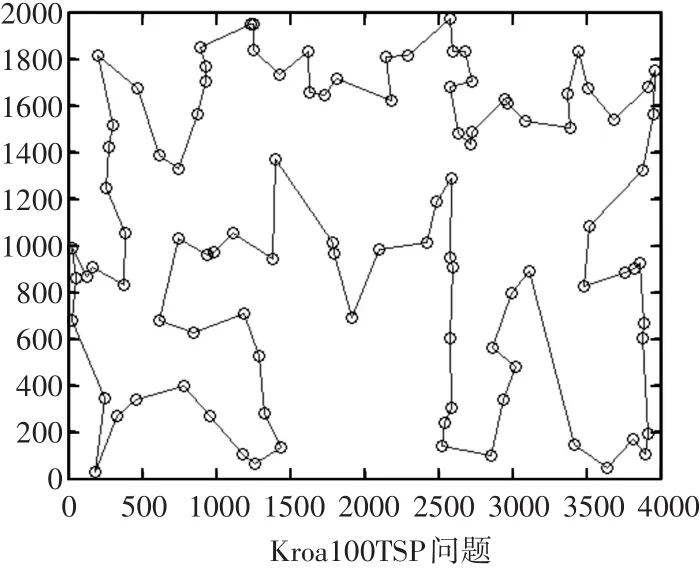
图9 本文算法优化Kroa100算例的路径图
图8~图12给出了本文算例Att48、kroa100、bier127、pr144、kroa200的最优路径图
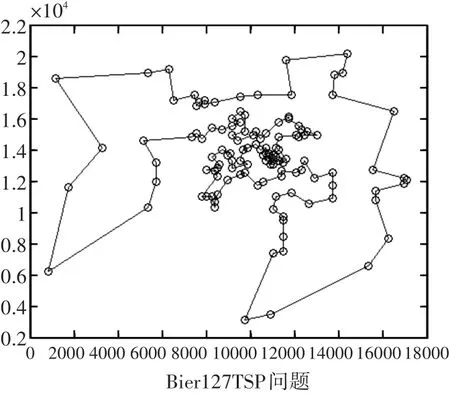
图10 本文算法优化Bier127算例的路径图
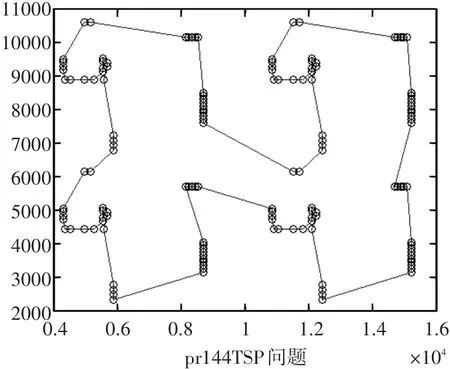
图11 本文算法优化pr144算例的路径图
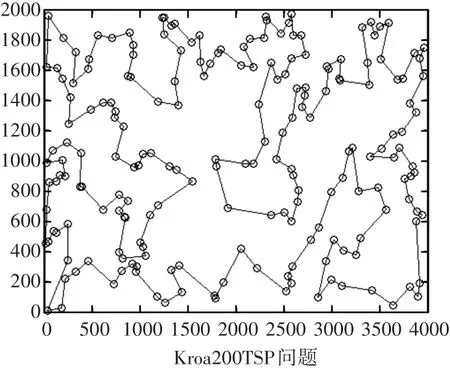
图12 本文算法优化Kroa200算例的路径图
6 结语
本文针对求解TSP问题,提出了一种求解TSP问题的离散型差分进化算法,通过特殊的编码方式和适当的参数测试设置,并首次将具有良好局部搜索能力的2-OPT算法与差分进化算法相融合,将仅用于求解连续域上优化问题算法拓展到用于解决离散组合优化问题。并选取了TSPLIB标准库中的几个14~200的TSP问题进行了测试仿真,仿真结果表明,在较少的进化代数的条件下,本文提出的算法所得到的最优解与TSPLIB中的最优解的偏差率都很低,说明本文算法在求解中小规模TSP问题时是有效可靠的。
今后的工作需将本算法进一步改进、优化以解决大规模的TSP问题及其它离散域上的复杂组合优化问题。
[1]李峰,庄东.运筹学[M].机械工业出版社,2014(4):243-255.LI Feng,ZHUANG Dong.Qperations Research[M].China Machine Press,2014,4:243-255.
[2]武妍,包建军.一种新的求解TSP的混合量子进化算法[J].计算机应用,2006,26(10):2433-2436.WU Yan,BAO Jianjun.New mixed quantum-inspired evolutionary algorithm for TSP[J].Computer Applications,2006,26(10):2433-2436.
[3]吴建辉,张兢,张小刚,等.分层协同进化免疫算法及其在 TSP 问题中的应用[J].电子学报,2011,39(2):336-340.WU Jianhui,ZHANG Jing,ZHANG Xiaogang,et al.Hierarchical Co-Evolution Immune Algorithm and Its Application on TSP[J].Acta Electronica Sinica,2011,39(2):336-340.
[4]尤梦丽,雷秀娟.改进的细菌觅食算法求解TSP问题[J].广 西 大 学 学 报 自 然 科 学 版 ,2013,38(6):1437-1439.YOU Mengli,LEI Xiujuan.An improved bacterial foraging algorithm for the traveling salesman problem[J].Journal of Guangxi University(Natural Science Edition),2013,38(6):1437-1439.
[5]张敬敏,马丽,李媛媛.求解TSP问题的改进混合蛙跳算法[J].计算机工程与应用,2012,48(11):47-50.ZHANG Jingmin,MA Li,LI Yuanyuan.Improved shuffled frog-leaping algorithm for traveling salesman problem[J].Computer Engineering and Applications,2012,48(11):47-50.
[6]曾宇容,王林,富庆亮.基于DE和PSO的混合智能算法及其在模糊EOQ模型中的应用[J].计算机应用研究,2012,29(2):438-441.ZENG Yurong,WANG Lin,FU Qingliang.Hybrid intelligent algorithm based on differential evolution and particle swarm optimization algorithm and its application in fuzzy EOQ model[J].Application Research of Computers,2012,29(2):438-441.
[7]WANG Lin,HE Jing,WU De-sheng,et al.A novel differential evolution algorithm for joint replenishment problem under interdependence and its application[J].International Journal of Production Economics,2012,135(1):190-198.
[8]Lin S.Kernigham B W.An effective heuristic algorithm for the travelling salesman problem[J].Operations Research,1973,21(2):4982-5161.
[9]Dorigo M.Stutzle T.Ant Colony Optimization[M].Massachusetts:MIT Press,London,England,2004:69-75.
[10]祝崇隽,刘民,吴澄,等.针对模糊需求的VRP的两种2-OPT算法[J].电子学报,2001,29(8):1035-1037.ZHU Chongjun,LIU Min,WU Cheng,et al.Two kinds of 2-opt algorithm for VRP with Fuzzy demand[J].Acta Electronica Sinica,2001,29(8):1035-1037.
[11]Peng Gang,Ichiro Ilmura,Shigeru Nakayma.An Evolutionary Multiple Heuristic with Genetic Local Search for Solving TSP[J].International Journal of Information Technology,2008,14(2):1-11.
[12]周永权,黄正新,刘洪霞.求解TSP问题的离散型萤火虫群优化算法[J].电子学报,2012,40(6):1164-1170.ZHOU Yongquan,HUANG Zhengxin,LIU Hongxia.Discrete Glowworm Swarm Optimization Algorithm for TSP Problem[J].Acta Electronica Sinica,2012,40(6):1164-1170.
[13]张长胜,孙吉贵,欧阳丹彤.一种自适应离散粒子群算法 及 其 应 用 研 究[J].电 子 学 报 ,2009,37(2):299-304.ZHANG Changsheng,SUN Jigui,OUYANG Dantong.A Self-Adaptive Discrete Particle Swarm Optimization Algorithm[J].Acta Electronica Sinica,2009,37(2):299-304.
[14]吴庆洪,张纪会,徐心和.具有变异特征的蚁群算法[J].计算机研究与发展,1999,36(10):1240-1245.WU Qinghong,ZHANG Jihui,XU Xinhe.An ant colony algorithm with mutation features[J].Journal of Computer Research and Development,1999,36(10):1240-1245.
[15] TSP Library.http://www.Iwr.uni-heideberg.de/iwr.compot/software/TSPLIB95/TSP.LIB.html.
[16]蔡之华,彭锦国,高伟,等.一种改进的求解TSP问题的演化算法[J].计算机学报,2005,28(5):823-829.CAI Zhihua,PENG jinguo,GAO Wei,et al.An Improved Evolutionary Algorithm for the Traveling Salesman Problem[J].Chinese Journal of Computers,2005,28(5):823-829.
[17]孙光福,李程俊,张冬梅,等.一种求解TSP问题的演化算法[J].计算机工程,2011,37(11):209-211.SUN Guangfu,LI Chengjun,ZHANG Dongmei,et al.Evolutionary Algorithm for Solving Traveling Salesman Problem[J].Computer Engineering,2011,37(11):209-211.
[18]王勇臻,陈燕,李桃迎.离散型细菌觅食算法求解TSP问题[J].计算机应用研究(网络版),2014,31(12):3642-3645.WANG Yongzhen,CHEN Yan,LI Taoying.Discrete bacteria foraging optimization algorithm for solving TSP[J].Application Research of Computers,2014,31(12):3642-3645.
[19]饶卫振,金淳,黄英艺.求解TSP问题的最近领域与插入混合算法[J].系统工程理论与实践,2011,31(8):1420-1426.RAO Weizhen,JIN Chun,HUANG Yingyi.Hybird algorithm,of the nearest neighbor and insertion for the traveling salesman problem[J].Systems Engineering-Theory&Practice,2011,31(8):1420-1426.
[20]张晓霞,唐立新.一种求解TSP问题的ACO&&SS算法设计[J].控制与决策,2008,23(7):765-766.ZHANG Xiaoxia,TANG Lixin.An ACO&SS algorithm for traveling salesman problem[J].Control and Decision,2008,23(7):762-766.
[21]王忠英,白艳萍,邱利霞.经过改进的求解TSP问题的蚁群算法[J].数学的实践与认识,2012,42(4):133-140.WANG Zhongying,BAI Yan-ping,YUE Lixia.An Improved Ant Colony Algorithm for Solving TSP Problems[J].Mathematics in Practice and Theory,2012,42(4):133-140.
[22]杜鹏桢,唐振民,孙研.一种面向对象的多角色蚁群算法及其TSP问题求解[J].控制与决策,2014,10(29):1733-1734.DU Pengzhen,TANG Zhenmin,SUN Yan.An object-oriented multi-role ant colony optimization algorithm for solving TSP problem[J].Control and Decision,2014,10(29):1733-1734.
A Discrete Differential Evolution Algorithm for TSP Problem
NING Guiying1CAO Dunqian2ZHOU Yongquan3
(1.Lushan College of Guangxi University Science and Technology,Liuzhou 545616)(2.College of Science,Guangxi University for Nationalities,Nanning 530006)(3.College of Information Science and Engineering,Guangxi University for Nationalities,Nanning 530006)
A discrete differential evolution algorithm is proposed for solving traveling salesman problem(TSP)in this article.In the algorithm,on the one hand,the differential evolution algorithm with a new coding method is used to solve a discrete TSP,which is often used to solve problems on a continuous domain.On the other hand,the 2-OPT algorithm is also introduced;the new algorithm combined the global search with the local search effectively.The classical TSP has been tested,the simulation results show that the proposed algorithm has strong stability and it is an effective method for solving TSP.
differential evolution,TSP,heuristic algorithm,fitness,2-OPT
TP183
10.3969/j.issn.1672-9722.2017.11.012
Class Number TP183
2017年5月9日,
2017年6月29日
国家自然科学基金项目(编号:61463007);2015年度广西高校科学技术研究项目(编号:KY2015YB521);2015年度广西教育厅科学研究项目(编号:KY2015YB081)资助。
宁桂英,女,硕士,讲师,研究方向:进化计算及应用。曹敦虔,男,硕士,讲师,研究方向:计算智能及多元样条函数。周永权,男,博士,教授,博导,研究方向:计算智能、智能优化、神经网络。

