在解题中促进学生学会研究的教学实践
——以“探索长方体和圆柱表面路径最短问题”为例

龚 辉

(江苏省太仓市沙溪第一中学 215421)

研究解题教学的文章较多，尤其是研究解题方法、解题技巧类的更多．事实上，目前较多存在解题教学功能异化的现象，比如过分追求应试的技巧、过分追求试题的偏、难、怪，大量存在通过刷题来提高成绩的现象，这些过分功利化的做法是导致数学学科饱受诟病的主要原因．

叶圣陶先生的教育思想之一是“教是为了不教”．试想，如果我们单纯地教学生知识，学生是很难达到不教而会的水平．因此，教什么就显得特别重要．我们要教会学生研究数学的方法、钻研数学的精神，从而慢慢地达到不教而教的目标．

“发展学生思维，教会学生思考，培养学生探究能力”是当今数学课堂教学改革的主要任务．我们要正确理解数学解题教学的教育功能，从培养学生的核心能力出发，让学生喜欢数学、懂得研究数学的方法，为学生的可持续发展奠定基础．

笔者就某次公开教学“探索长方体和圆柱表面路径最短问题”为例，探讨促进学生学会研究、学会学习的方法，以期抛砖引玉，与同行交流．

1 学会转化——知识从哪里来

布鲁姆在《教学目标分类学》明确指出，数学转化思想是“把问题元素从一种形式向另一种形式转化的能力”．在数学学习中，学会利用转化思想明确“知识从哪里来”是非常重要的．

在本课例的教学中，涉及把立体图形转化为平面图形，然后对转化后的平面图形问题用平面几何知识分析求解的过程．这是一种降低所研究问题的维度从而解决问题的方法，例如多元方程组利用消元的方法转化为一元方程；在研究立体图形时，将高维的图形转化为低维的图形等．

笔者在教学的第一个活动环节中，设计了如下的问题串：

(1)如图1，棱长为1的正方体ABCD—A1B1C1D1，一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点C1，求爬行的最短距离．

图1

(2)如图2，圆柱形木块的高为8，底面半径为2，下底面A点处有一蚂蚁，想吃到上底面相对的C点处的食物，需沿圆柱的表面爬行的最短路程是多少？(π取近似值3)．

图2

解决这两个问题，首先要明确最短路径问题的解决策略是“两点之间，线段最短”；然后引导学生思考路径的大致形态，明确不可能是线段，而应该分别是折线和曲线；最后再研究如何将不在同一平面内的折线和曲线转化到同一个平面内．在问题设计的梯度方面，从正方体问题变式为圆柱问题，由直到曲，不断深入，体现了变式教学在数学解题和数学研究中的重要作用．

在问题1的处理上，笔者首先引导学生思考运用“两点之间，线段最短”解决路径最短问题的前提条件是什么？学生明白“在同一平面内”这个前提之后，再进行大胆猜想：如何将立体图形转化为平面图形，使得点A和点C1在同一个平面内？在师生互动中归纳解决的方法：将正方体的表面展开．随后，教师引导学生作深入的思考：是否需要完全展开，怎么展开？最后，教师利用Geogebra软件进行动画演示，直观地展现出立体图形平面化的过程．

在问题2的处理环节中，笔者引导学生继续用降维转化的方法，学生明白“我要做什么”、“我已经会什么”、“我该怎么做”，从而主动探究解决圆柱问题的方法：将圆柱的侧面展开，使点A、C在同一个平面内，从而可以运用“两点之间，线段最短”解决问题．

在教学实施过程中，笔者欣喜地发现，学生在掌握了正方体的转化策略之后，只需在教师的略微引导下，便可顺畅地解决圆柱的表面路径最短问题．可见，教会学生研究数学问题的方法是非常重要的，解题教学的境界和目的，应该从“做题目”向“做实验”转变，并最终向“做研究”深入．

2 学会生长——知识往哪里去

G·波利亚(George Polya)在《怎样解题》一文中提出了著名的解题表理论，其中，在“回顾反思”环节，波利亚指出，解题后要思考你能否用别的方法导出这个结果？你能不能一下子看出它来？你能不能把这个结果或方法用于其他的问题？

然而，在数学教学中以追求数学题目的答案为终极目标的现象较为普遍，解题教学中就题论题者较多．如何充分利用数学题目这一思维的载体，充分发挥它的教育价值？若能从研究的角度看解题，真可谓研究无处不在，只是我们平时浅尝辄止罢了．因此，解题后的再思考，是知识再生长的过程，再生长的不仅是数量，还有深度，更是研究数学的一种态度．

在第二个活动环节中，笔者设计了如下两个问题：

(1)如图3，长方体的底面为边长为1的正方形，高为2，一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点C1，求最短距离．

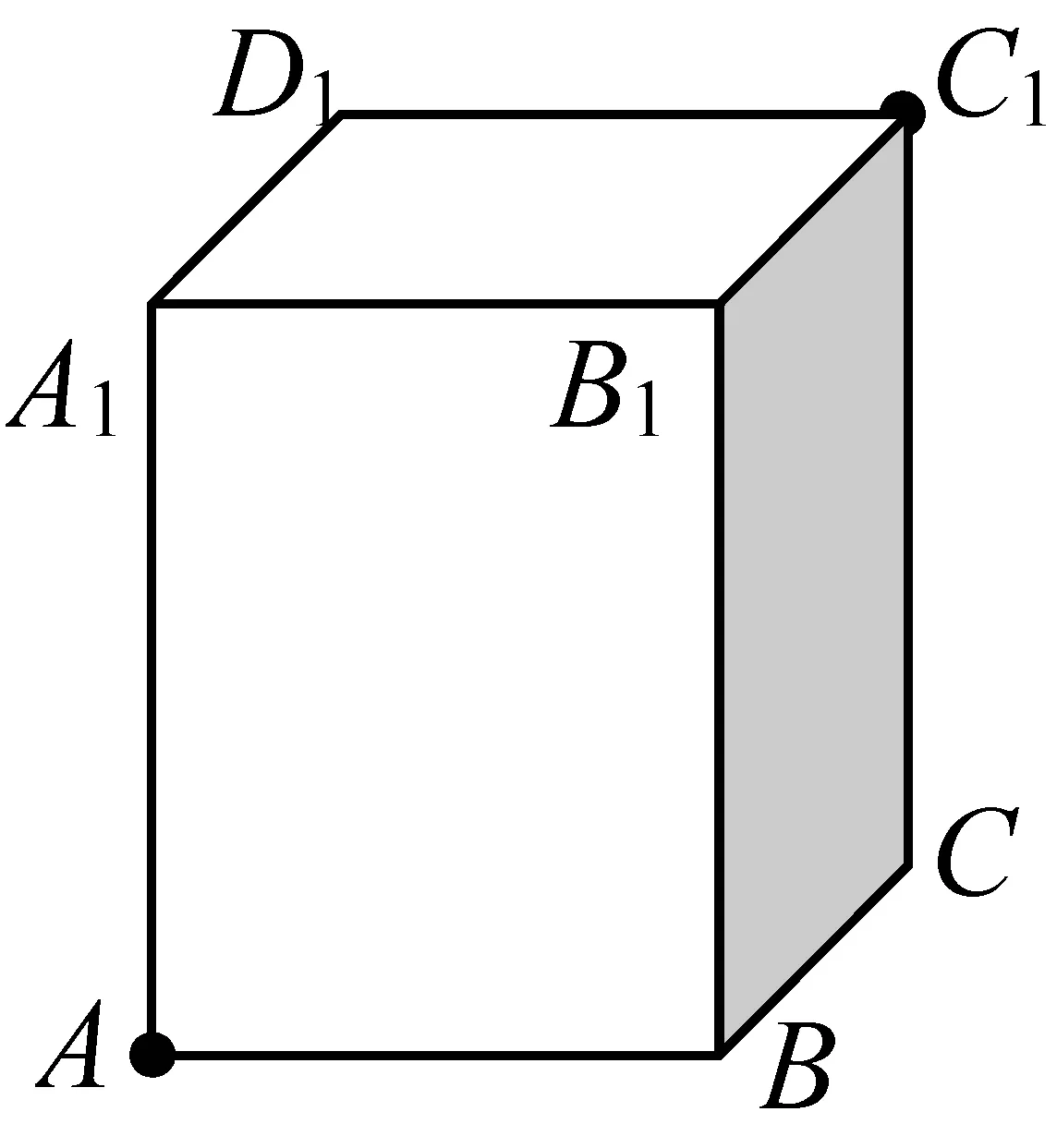
图3

图4

(2)变式：如图4，将上题中长方体的底面边长改为2的正方形，高改为1，求点A到点C1的最短距离.

在活动一的教学中，学生已经能够运用翻转一个面将立体图形转化为平面图形，从而解决正方体中相关问题的方法．设计这两个问题的主要目的是引导学生不要满足于活动一所获得的方法，更要善于对结论进行推广，并在变式中发现的问题：不同的学生用不同的表面展开方式，计算得到的结果是不一致的．这种认知上的矛盾冲突，非常容易激发学生的学习热情和探索欲望，达到了“学起于思，思源于疑”的目的．

通过这两个问题的研究，结合Geogebra软件的动画演示，学生明白了将长方体的两个表面展开在同一个平面内共有12种方法，其中能够使点A和点C1在同一平面内的有6种方法，6种方法中又有3种情况的本质是相同的．

知识再生长的目标，是能够从特殊情况中归纳出一般规律，并能够用数学严密的逻辑方法去证明．笔者在教学中追问：对于任意边长的长方体，我们能否根据其边长直接明确翻转的方式，从而不必讨论而求出最短的路径？

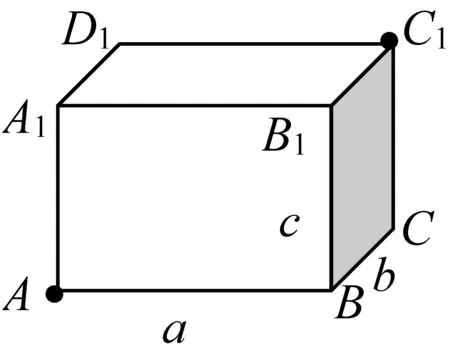
图5

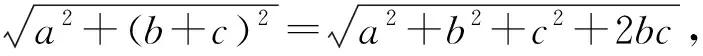
数学的魅力在于数学答案的封闭性和数学研究过程的开放性．这种开放是需要教师在教学中不断地引导学生进行深入的尝试与思考，将拓展与变式常态化，不要仅仅满足于数学试题的解答，要提高到数学问题的解决，明白学得的数学知识该往哪里去，使学生养成一种自觉的思维习惯和良好的思维品质．

3 学会创新——知识的再认识

著名国学大师王国维在《人间词话》中写道：“诗人对宇宙人生，须入乎其内，又须出乎其外.入乎其内，故能写之；出乎其外，故能观之.”数学解题教学最终应该达到跳出题目看题目的境界，要让学生从解惑中生疑，从而引导学生不断地深入研究，不断地提出新的问题．“出乎其外”，是对学生发散性思维和批判性思维的培养．

在第三个活动环节中，笔者出示了下面的问题：

如图6，圆柱形木块的高为7，底面半径为8，下底面A点处有一蚂蚁，想吃到上底面相对的C点处的食物，需沿圆柱表面爬行的最短路程是多少？(π取近似值3)．

图6

本小题是活动一中圆柱表面最短路径问题的变式，学生按侧面展开的方式可以得到最短路径长为25．然后，教师提问：有没有更短的路径呢？显然，学生陷入了深深的思维冲突之中：刚才不是已经用侧面展开的方法解决了最短问题，怎么还会更短呢？

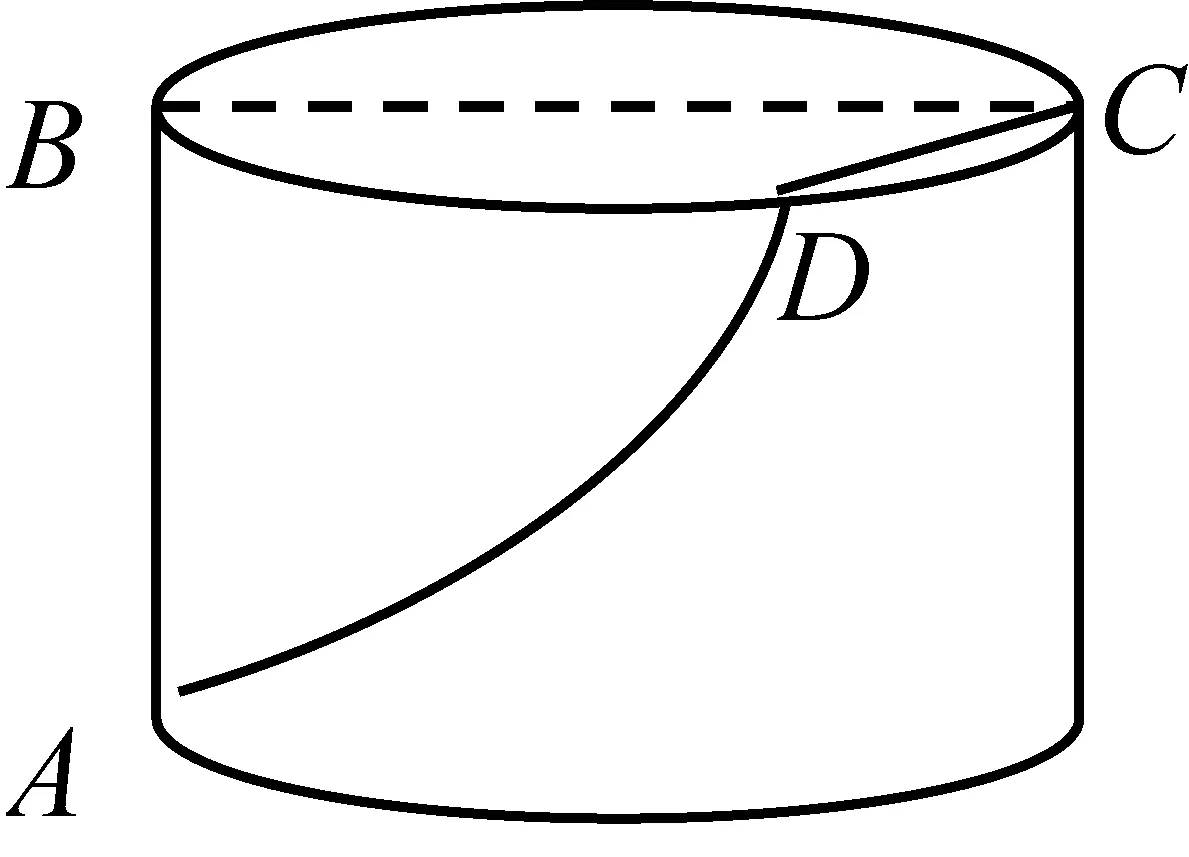
图7

本题还可以引导学有余力的学生在课外再作深入的研究：如图7，若蚂蚁一部分走侧面曲线AD，一部分走底面线段CD，路程会不会比前面两种都更短呢？

本节课的教学目的不只在于最终得到了什么公式或是结论，关键是从公式和结论的探究活动中学会了研究数学问题的一般方法，因此，过程更胜于结果．

阿弗烈·诺夫·怀德海(Alfred North Whitehead)说：“把学校学到的知识忘掉，剩下的那一部分才是教育”．就数学教学而言，若干年后忘掉的是答案、公式和结论，而忘不掉的，则是解题教学过程中蕴含的“为学生发展”而存在的数学研究方法和数学理性精神．因此，教师应力求让研究成为数学课堂教学的常态，使数学研究逐步成为学生学习的自觉行为乃至学习习惯，使学生的科学精神和研究能力得到长足的进步．