时态德摩根逻辑的语义与证明论*

梁飞

中山大学逻辑与认知研究所

中山大学哲学系

liangf25@mail2.sysu.edu.cn

1 引言

德摩根代数又称拟布尔代数（quasi-Boolean algebras）、分配i-格（distributive i-lattice），它是带德摩根否定的分配格，是布尔代数的弱化。德摩根代数最早由莫斯尔（G.Moisil）在1935年提出（[19]），之后它在逻辑与代数领域中得到广泛研究（[1,2,6,20]）。类似于二值代数与布尔代数的关系，德摩根代数与四值代数4（见下图）关系密切，卡尔曼（J.A.Kalman）（[17]）证明了4（[17]中为D）是德摩根代数的一个子直不可归约代数（subdirectly irreducible algebras），每一个德摩根代数均能嵌入4的直积（direct product）中。

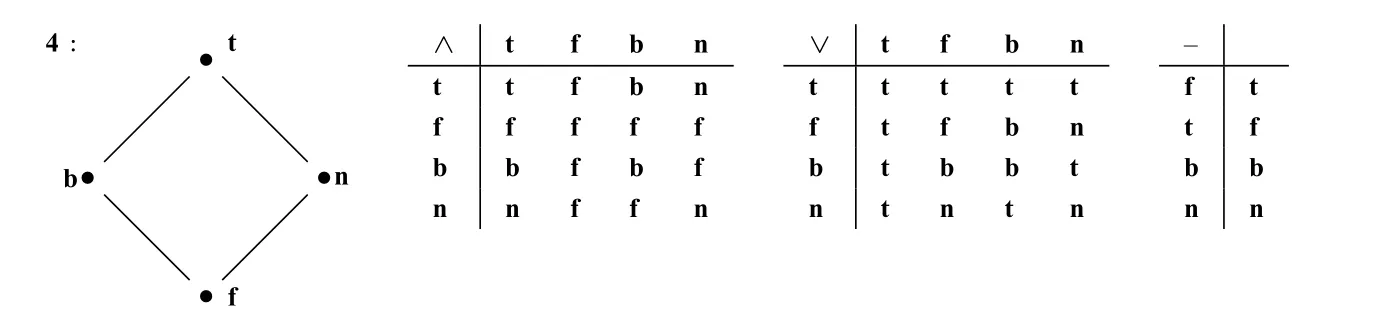
贝尔纳普（N.Belnap）在研究相干性与推衍（entailment）时（[21]）认识到德摩根代数是一度蕴涵（first-degree implication）系统Rfde的代数语义模型。邓恩（M.Dunn）在[8]中证明了Rfde相对于4是可靠且完全的。随后，在[3,4]中，贝尔纳普创造性地给出了四值代数的直观解释。他将n解释为“缺乏信息”，将b解释为“矛盾信息”。邓恩在此基础上，进一步给出了四值逻辑的关系语义模型。（[7,9,10]）贝尔纳普和邓恩的这一系列工作使四值逻辑在逻辑学、计算机科学、人工智能等领域均受到大量关注，四值逻辑也被称作“贝尔纳普-邓恩”（Belnap-Dunn）逻辑。

如果在布尔代数上加入一元时态算子G（将来总是…）、H（过去总是…）及其对偶算子F（过去可能…）、P（将来可能…），那么所得到的结构就是时态代数（Tense algebras）。时态代数所对应的逻辑是极小时态逻辑Kt。相应地，费加罗（A.V.Figallo）与佩莱特（G.Pelaitay）研究了带有一元时态算子的德摩根代数（[11]），称之为时态德摩根代数（Tense De Morgan algebras）。他们从代数的角度证明了时态德摩根代数的表示定理、拓扑对偶（duality）定理，并在此基础上刻画了该结构的同余（congruence）关系。本文将从逻辑的角度研究时态德摩根代数。首先给出时态德摩根代数所对应的逻辑：时态德摩根逻辑（DMt）。其次给出该逻辑的关系语义，证明DMt在该语义下的可靠性与完全性。最后，本文还从证明论的角度研究时态德摩根逻辑的显示演算（display calculus），并证明该演算切割消除定理及子结构性质。

2 时态德摩根逻辑的代数语义

定义1([11])一个德摩根代数（简称DM-代数）是A=(A,∧,∨,～,1,0)，其中(A,∧,∨,1,0)是有界分配格，且满足以下4个条件：对任意a,b∈A，

定义2([11])一个时态德摩根代数（简称DMt-代数）是A=(A,∧,∨,～,G,H,1,0)，其中(A,∧,∨,～,1,0)是德摩根代数，G,H是定义在A上的一元算子且满足以下条件:对任意a,b∈A，

(T1)G(1)=1，H(1)=1；

(T2)G(a∧b)=G(a)∧G(b)，H(a∧b)=H(a)∧H(b)；

(T3)a≤GP(a),a≤HF(a)，其中F(a):=～G～(a),P(a):=～H～(a)；

(T4)G(a∨b)≤G(a)∨F(b)，H(a∨b)≤H(a)∨P(b)。

DMt-代数构成了时态德摩根代数簇，下文中我们用DMT代表该代数簇。

推论1([11])以下命题在DMt-代数中成立：对任意a,b∈A，

(T5)如果a≤b，那么G(a)≤G(b)且H(a)≤H(b)；

(T6)如果a≤b，那么P(a)≤P(b)且F(a)≤F(b)；

(T7)F(0)=0，P(0)=0；

(T8)F(a∨b)=F(a)∨F(b)，P(a∨b)=P(a)∨P(b)；

(T9)PG(a)≤a，FH(a)≤a；

(T10)G(a)∧F(b)≤F(a∧b),H(a)∧P(b)≤P(a∧b)。

易知，若DMt-代数满足a∧～a≤0或1≤a∨～a，则其为时态代数。

定义3(时态德摩根逻辑语言)给定可数无穷原子命题集Prop，时态德摩根逻辑（记作DMt）语言递归定义如下：

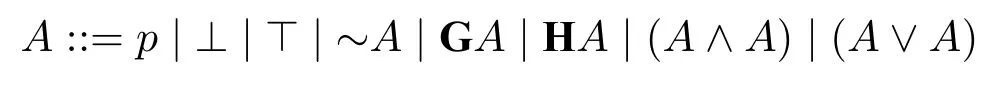
其中p∈Prop。下文中我们用Fm代表DMt公式集。

令F::=～G～，P::=～H～。

定义4(公理系统)DMt公理系统定义如下：

1.公理

2.规则

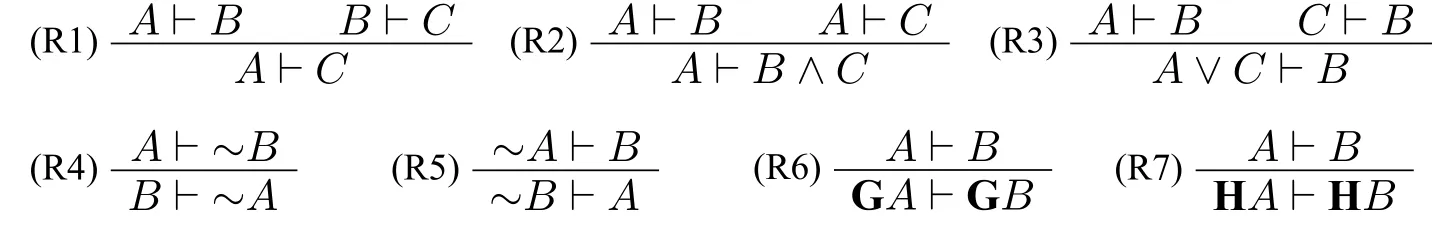
推论2以下矢列在DMt中可证：

定义5称矢列A⊢B在系统S中可证（记作A⊢SB），如果存在一个由公理开始的证明序列，序列中的每一个元素要么是公理，要么由规则得到。

定义6(赋值及有效)任给时态德摩根代数A=(A,∧,∨,～,G,H,1,0)，称σ:Prop→A是A中的赋值函数。对任意A∈Fm，Aσ递归定义如下：

称A⊢B在代数A中有效（记作A|=A⊢B），如果对任意A中赋值σ，Aσ≤Bσ，其中≤是A中的格序。任给代数类K，称A⊢B在代数类K中有效(记作:K|=A⊢B)，如果对任意A∈K，A|=A⊢B。

定理1任给矢列A⊢B，A⊢DMtB当且仅当DMT|=A⊢B。

证明：根据林登鲍姆-塔斯基（Lindenbaum-Tarski）证明易得。 □

下面我们证明DMt的系统性质。

定义7(推演)任给Γ∪{A}⊆Fm，称Γ⊢A是DMt的推演，如果存在有穷集合Δ⊆Γ，使得∧Δ⊢A可证。

推论3以下命题成立：

(1)如果Γ⊢A且Γ⊢B，那么Γ⊢A∧B；

(2)如果Γ∪{A}⊢C且Γ∪{B}⊢C，那么Γ∪{A∨B}⊢C；

(3)如果Γ⊢A且Δ∪{A}⊢C，那么Γ∪Δ⊢C。

证明：(1)设Γ⊢A，据推演定义可知，存在有穷集Γ1⊆Γ，使得∧Γ1⊢A(i)。同理可得，存在有穷集Γ2⊆Γ，使得∧Γ2⊢B。据(A6)、(R1)和(i)得∧Γ1∧∧Γ2⊢A，同理有∧Γ1∧∧Γ2⊢B。据(R2)，∧Γ1∧∧Γ2⊢A∧B，因为Γ1∪Γ2⊆Γ且有穷，得证。(2)与(3)证明与之类似，从略。 □

下面给出理论与对偶理论的定义及性质。

定义8任给Σ⊆Fm，称Σ是DMt的理论，如果Σ满足以下条件:

(1)Σ/=∅；

(2)如果A∈Σ且A⊢B，那么B∈Σ；

(3)如果A∈Σ且B∈Σ，那么A∧B∈Σ。

定义9任给Σ∂⊆Fm，称Σ∂是DMt的对偶理论，如果Σ∂满足以下条件:

(1)Σ∂/=∅；

(2)B∈Σ∂且A⊢B，那么A∈Σ∂；

(3)如果A∈Σ∂且B∈Σ∂，那么A∨B∈Σ∂。

定义10设Σ是DMt的理论，称Σ是DMt的一致素理论，如果Σ满足以下条件:

(1)⊥/∈Σ；

(2)如果A∨B∈Σ，那么A∈Σ或B∈Σ。

推论4如果Γ是一致素理论，那么是对偶理论，其中Γ是Γ的补集。

证明：设B∈且A⊢B，欲证A∈。假设A∈/，那么A∈Γ。故B∈Γ，且B∈/Γ，与题设条件矛盾，故A∈。如果A∈且B∈，假设A∨B∈/，那么A∨B∈Γ，因为Γ是素理论，故A∈Γ或B∈Γ，矛盾。 □

引理1如果Γ⊬B且⊥/∈Γ，那么存在一致素理论Σ，使得Γ⊆Σ且B/∈Σ。

证明：枚举所有的DMt公式：A0,A1,...,Σ的构造如下：

根据构造，易知Σ⊬B，且⊥/∈Σ。现证Σ是一个理论。

如果Ai∈Σ且Ai⊢Aj，假设Aj/∈Σ，那么Σj∪{Aj}⊢B。因为Ai⊢Aj，据推论3(3)，得Σj∪{Ai}⊢B，故Σ⊢B，矛盾。假设Ai,Aj∈Σ且Ai∧Aj/∈Σ，易知Σij∪{Ai∧Aj}⊢B。不失一般性，设i≤j，根据构造可知Ai,Aj∈Σj，所以Σj⊢Ai且Σj⊢Aj，据推论3(1)，Σj⊢Ai∧Aj。据推论3(3)，得Σij∪Σj⊢B，故Σ⊢B，矛盾。综上，Σ是一个理论。

现证Σ是素理论。假设Ai∨Aj∈Σ，Ai/∈Σ且Aj/∈Σ。不失一般性，设i≤j，那么Σj∪{Ai}⊢B且Σj∪{Aj}⊢B。据推论3(2)有Σj∪{Ai∨Aj}⊢B，又因为Σj∪{Ai∨Aj}⊆Σ，所以Σ⊢B，矛盾。 □

类似地，可证明引理2。

引理2如果Γ是一个一致理论，Δ是对偶理论，Γ∩Δ=∅，那么存在一致素理论Σ，使得Γ⊆Σ且Σ∩Δ=∅。

引理3对任意Γ⊆Fm，如果Γ/=∅且对∨封闭，那么存在对偶理论Σ∂，使得Γ⊆Σ∂。

证明：令Σ∂={A∈Fm|A⊢B，其中B∈Γ}。显然，Γ⊆Σ∂，Σ∂/=∅。下证Σ∂是对偶理论。设A1∈Σ∂且A2⊢A1，据构造存在B∈Γ，A1⊢B。据(R1)得，A2⊢B，故A1∈Σ∂。设A1∈Σ∂且A2∈Σ∂，据构造存在B1,B2∈Γ，A1⊢B1且A2⊢B2，据(A9)(R1)得，A1⊢B1∨B2且A2⊢B1∨B2，据(R3)，A1∨A2⊢B1∨B2。又因Γ对∨封闭，故B1∨B2∈Γ，故A1∨A2∈Σ∂。 □

3 时态德摩根逻辑的关系语义

本节我们将给出DMt的关系语义，定义其框架、模型及满足关系，进而证明DMt的可靠性与完全性。

定义11(框架及模型)称F=(W,≤,g,R,R-1)是时态德摩根框架，如果F满足以下条件:对任意w1,w2∈W,

(F1)(W,≤)是一个偏序结构；

(F2)g:W→W，使得:如果w1≤w2，那么g(w2)≤g(w1)；

(F3)对任意w∈W，gg(w)=w；

(F4)(≤◦R)⊆(R◦≤)；

(F5)(≤◦R-1)⊆(R-1◦≤)；

(F6)如果(w1,w2)∈R，那么(g(w1),g(w2))∈R。

定义赋值V:Prop→℘(W)↑，其中℘(W)↑意为：如果w1∈℘(W)且w1≤w2，那么w2∈℘(W)，并称M=(F,V)是时态德摩根模型。

框架中g函数为对合函数（involutive），最早由拉西娃（H.Rasiowa）在[6]中研究德摩根代数的表示定理时提出，用以解释德摩根否定。需要注意的是，因为德摩根逻辑中矛盾律与排中律的失效，各可能世界之间并不是反链（anti-chain）关系，而是偏序关系，因此模型中的赋值需要对该偏序关系保持。(F4)与(F5)保证了该框架所定义的赋值是上升集，(F6)保证了G与F，H与P之间能够相互定义。

定义12(满足及有效)对任意公式A∈Fm，满足关系定义如下：

(1)M,w⊨⊤；

(2)M,w⊭⊥；

(3)M,w⊨p当且仅当w∈V(p)；

(4)M,w⊨～A当且仅当g(w)⊭A；

(5)M,w⊨GA当且仅当对任意w′∈W，如果w′∈R(w)，那么w′⊨A；

(6)M,w⊨HA当且仅当对任意w′∈W，如果w′∈R-1(w)，那么w′⊨A；

(7)M,w⊨A∧B当且仅当w⊨A且w⊨B；

(8)M,w⊨A∨B当且仅当w⊨A或w⊨B。

根据F,P定义，易知：

(9)M,w⊨FA当且仅当存在v∈W，使得v∈R(w)且v⊨A；

(10)M,w⊨PA当且仅当存在v∈W，使得v∈R-1(w)且v⊨A。

赋值V:Prop→℘(W)↑可唯一地扩展至V′:Fm→℘(W)，故M,w⊨A当且仅当w∈V′(A)。若V′(A)⊆V′(B)，则称模型M满足A⊢B。若对F上的任意模型M，M满足A⊢B，则称A⊢B在框架类F上有效，记作A⊨B。

命题1对任意w∈W，如果w∈V′(A)且w≤w′∈W，那么w′∈V′(A)。

证明：施归纳于公式A的复杂度。当A=p,⊥,⊤时，据满足关系定义可得。当A=A1∧A2或A=A1∨A2时，据归纳假设易得。

当A=～B时，w∈V′(～B)。据满足关系定义g(w)/∈V′(B)。又因为w≤w′，据(F2)，得g(w′)≤g(w)。据归纳假设，g(w′)/∈V′(B)，即w′∈V′(～B)。

当A=GB时，w∈V′(GB)。据满足关系定义R(w)⊆V′(B)。对任意x∈W，如果x∈R(w′)，因为w≤w′，那么(w,x)∈(≤◦R)。据(F4)，存在z∈W使得z∈R(w)且z≤x。易见z∈V′(B)，据归纳假设得x∈V′(B)，故R(w′)⊆V′(B)，即w′∈V′(GB)。A=HB时证明与之类似。 □

定义13(典范框架与典范模型)称Fc=(Wc,⊆,g,RG,RH)为一个时态德摩根典范框架，如果Fc满足以下条件:对任意X,Y∈Wc,

(C1)Wc={X:X是一致素理论}；

(C2)g(X)={A∈Fm|～A/∈X}；

(C3)(X,Y)∈RG当且仅当G-(X)⊆Y⊆F-(X)；

(C4)(X,Y)∈RH当且仅当H-(X)⊆Y⊆P-(X)。

定义赋值Vc:Prop→℘(Wc),Vc(p)={X∈Wc|p∈X}，并称Mc=(Fc,Vc)为一个时态德摩根典范模型。

上述定义中，G-(X)={A|GA∈X}，F-(X),H-(X),P-(X)定义类似。由推论 2的 (7)、(9)、(11)、(13)及 (R6)、(R7)可得：

推论5G-(X)，H-(X)是理论，是对偶理论。

为了证明系统的完全性，我们首先来证明上述定义下的框架是一个时态德摩根框架。显然，(Wc,⊆)是一个偏序结构，(F1)成立。下证(F2)-(F6)成立。

引理4对任意X,Y∈Wc，以下命题成立：

(1)g(X)∈Wc，且gg(X)=X；

(2)如果X⊆Y，那么g(Y)⊆g(X)。

证明：(1)欲证g(X)∈Wc，即证明g(X)是一致素理论。设⊥∈g(X)，据定义～⊥/∈X。又据推论2(2)，得⊤/∈X。因为X/=∅及(A2)，⊤∈X，矛盾。故g(X)是一致的。

现证g(X)是一个理论。设A∈g(X)且A⊢B(i)，那么～A/∈X，根据推论2(4)、(R1)、(R4)和(i)得：～B⊢～A，故～B/∈X，所以B∈g(X)。设A∈g(X)那么～A/∈X，同理可得，B∈g(X)那么～B/∈X。因为X是素理论，所以～A∨～B/∈X。根据推论2(6)得～(A∧B)/∈X，即(A∧B)∈g(X)。

现证g(X)是素理论。设A∨B∈g(X)，那么～(A∨B)/∈g(X)。据推论2(5)得：～A∧～B/∈g(X)。因为X是理论，所以～A/∈g(X)或～B/∈g(X)，即A∈g(X)或B∈g(X)。故g(X)是素理论。

下证gg(X)=X。

(⊆)：设A∈gg(X)，那么～A/∈g(X)，那么～～A∈X，根据推论2(1)得：A∈X。

(⊇)：设A∈X，根据推论2(4)及X可得：～～A∈X。据定义有～A/∈g(X)，那么A∈gg(X)。

(2)设X⊆Y且A∈g(Y)，据定义有～A/∈Y，那么～A/∈X，即A∈g(X)。□

引理5任取X,Y∈Wc，(X,Y)∈RG当且仅当(Y,X)∈RH。

证明：(⇒)如果(X,Y)∈RG，即G-X⊆Y⊆F-X，假设HA∈Y，欲证A∈X。由HA∈Y可得：HA∈F-X。据定义有：FHA∈X，据(A13)得A∈X，即H-Y⊆X。现证明X⊆P-Y，即设A∈X，欲证PA∈Y。据(A10)，得GPA∈X。据定义，有PA∈G-X，故PA∈Y。(⇐)证明类似，从略。 □

引理6任取X,Y∈Wc，以下命题成立：

(3)如果(X,Y)∈RG，那么(g(X),g(Y))∈RG。

证明：(1)令X,Z,Y∈Wc，X⊆Z且(Z,Y)∈RG，那么G-(Z)⊆Y⊆F-(Z)，据定义得，G-(X)⊆G-(Z)⊆Y。令Δ′={A0∨...∨An∨B0∨...∨Bm|显然且Δ′对∨封闭。据引理3得，存在对偶理论Δ，使得Δ′⊆Δ。下证:G-(X)∩Δ=∅。

假设G-(X)∩Δ/=∅，那么存在A∈G-(X)(i)且A∈Δ。据Δ构造可得，存在D=A0∨...∨An∨B0∨...∨Bm∈Δ′，使得A⊢D，其中A0...An∈B0...Bm∈又据引理4和推论5，A0∨...∨An∈Y(ii)且B0∨...∨Bm∈F-(X)(iii)。据(R6)，GA⊢GD，即GA⊢G(A0∨...∨An∨B0∨...∨Bm)。由 (i)可得，GA∈X，故 G(A0∨...∨An∨B0∨...∨Bm)∈X。据 (A14)，G(A0∨...∨An)∨F(B0∨...∨Bm)∈X。因为X是素理论，故G(A0∨...∨An)∈X或F(B0∨...∨Bm)∈X。

如果G(A0∨...∨An)∈X，那么A0∨...∨An∈G-(X)，据题设条件，A0∨...∨An∈Y，即矛盾于(ii)。如果F(B0∨...∨Bm)∈X，那么B0∨...∨Bm∈F-(X)，即矛盾于 (iii)。故G-(X)∩Δ = ∅，据引理2可得：存在一致素理论Σ，使得G-(X)⊆Σ且Σ∩Δ=∅，故且因此G-(X)⊆Σ⊆F-(X)且Σ⊆Y。故(⊆◦RG)⊆(RG◦⊆)。(2)与(1)证明类似，从略。

(3)设(X,Y)∈RG，那么G-(X)⊆Y⊆F-(X)。欲证G-(g(X))⊆g(Y)⊆F-(g(X))。假设G-(g(X))⊈g(Y)，那么存在A∈G-(g(X))且A/∈g(Y)，根据定义有：～GA/∈X且～A∈Y。据题设条件可知F～A∈X。因为F～A⊢～GA，所以～GA∈X，矛盾。同理可证，g(Y)⊆F-(g(X))。 □

由引理2与引理5立得：

命题2时态德摩根典范框架是时态德摩根框架。

引理7任给X∈Wc，Mc,X⊨A当且仅当A∈X。

证明：施归纳于公式A的复杂度。A=p,⊤,⊥时，据典范模型定义可得。A=A1∨A2或A1∧A2时，据归纳假设易得，证明从略。

当A=～B时，Mc,X⊨～B，据满足关系定义，Mc,g(X)⊭B。据归纳假设，B∈g(X)，又据g定义，～B/∈X。

当A=GB时，先证从右向左。设Mc,X⊭GB，据满足关系定义，存在Y∈Wc，Y∈RG(X)且Mc,Y⊭B。据RG定义，G-(X)⊆Y⊆F-(X)且Mc,Y⊭B。据归纳假设，B/∈Y，故B/∈G-(X)，据定义，得GB/∈X。

再证从左向右。设GB/∈X，那么B/∈G-X。令与引理6(1)证明类似，存在对偶理论Δ，使得Δ′⊆Δ且G-(X)∩Δ =∅。据推论2，可知存在一致素理论Y，使得G-(X)⊆Y且Y∩Δ=∅，故Y∩F-(X)=∅。因此G-(X)⊆Y⊆F-(X)且B/∈Y。据归纳假设及RG定义，Mc,X⊭GB。

当A=HB时，证明与之类似，从略。 □

定理2A⊢B当且仅当A⊨B。

证明：(⇒)即可靠性证明，证明方法如常。这里仅举例说明：

如果A⊢GPA，任给模型M，欲证V′(A)⊆V′(GPA)。即证明：任取w∈W，如果w∈V′(A)，那么w∈V′(GPA)。假设w/∈V′(GPA)，据满足关系得R(w)⊈V′(PA)，即存在z∈R(w)且z/∈V′(PA)。那么R-1(z)∩V′(A)=∅，故w/∈R-1(z)，这与z∈R(w)矛盾。

如果(R4)成立，任给模型M，欲证：如果V′(A)⊆V′(～B)，那么V′(B)⊆V′(～A)。假设V′(B)⊈V′(～A)，即存在w∈V′(B)且w/∈V′(～A)。据满足关系得g(w)∈V′(A)，那么据题设条件得g(w)∈V′(～B)。故gg(w)/∈V′(B)，据(F3)，w/∈V′(B)，与假设条件矛盾。

(⇐)假设A⊬B，根据引理1，存在一致素理论U，使得A∈X且B/∈X。据引理7，存在典范模型Mc，Mc,X⊨A且Mc,X⊭B，即A⊭B。 □

4 时态德摩根逻辑的显示演算

显示演算是贝尔纳普在[5]提出的，它是对甘岑系统的一般化研究。其基本思想是，区分公式与结构以及命题联结词与结构算子。根据结构算子出现的位置（矢列左边或右边）的不同，每一个结构算子被解释为不同的联结词。因为显示规则的存在，每一个结构都能够通过显示规则单独地出现在矢列的左边或右边，即显示性质。这样使系统地研究切割消除的证明成为可能。贝尔纳普提出了满足显示演算特点的8个条件(C1)-(C8)，分别为：

(C1)出现在规则(R)前提中的每一个公式都是(R)结论中某个公式的子公式。

(C2)同余（congruent）参数是相同结构的出现。

(C3)每一个参数最多与结论中一个组成部分为同余关系，等价地，结论中任意两个组成部分均不为同余关系。

(C4)同余参数要么是矢列的整个前件，要么是矢列的整个后件。

(C5)如果出现在规则(R)结论中的公式不是参数的，那么这个公式要么是矢列的整个前件，要么是矢列的整个后件。这样的公式称为规则(R)的主要（principal）公式。

(C6/7)用任意结构对规则(R)中同余参数同时进行替换，所得结果仍是规则(R)。

(C8)如果规则(R)与规则(R′)的结论分别为:X⊢A，A⊢Y，其中A是两个规则的主要公式，且对这两个结论使用切割（Cut）规则得X⊢Y。那么X⊢Y要么与X⊢A或A⊢Y相同，要么可以对规则(R)与规则(R′)的前提使用切割规则，其中切割公式是A的真子公式。

除(C8)外，每条性质均可根据系统规则的形式来判断。相较于甘岑系统，这样的形式极大的简化了切割可消除的证明。在贝尔纳普之后，克拉赫特（M.Kracht）系统地研究了显示演算的表达力及限度。（[18]）万辛（H.Wansing）（[22,23]），戈莱（R.Goré）（[12,13]），帕米迦娜（A.Palmigiano）和格里克（G.Greco）（[14-16]）进一步拓宽了显示演算的领域，分别研究了模态逻辑，子结构逻辑以及多类型显示演算。

定义14(语言)给定可数无穷的原子命题集Prop，显示演算（记作D.DMt）公式递归定义如下：

其中，♦::=～□～,♢::=～■～。D.DMt结构递归定义如下：

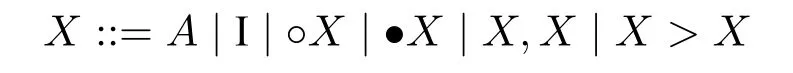
下文中我们用Stru指代D.DMt系统中结构的集合。D.DMt结构算子的解释如下：

为了使系统具有显示性质，D.DMt系统引入了A→A和A.-A，相应地，在结构中引入了X＞X。在下文中我们将证明该系统是DMt的保守扩张。

定义15(规则)D.DMt的规则如下：

下面首先证明D.DMt是DMt的保守扩张，即对任意A,B∈Fm,A⊢DMtB，当且仅当，A⊢D.DMtB。从左至右易得，只需证明DMt系统的公理及规则在D.DMt中可证。为了证明反方向成立，我们证明其逆否命题。证明思路如下:首先证明，D.DMt相对于DMt框架是可靠的。根据结构在矢列左边与右边的不同解释，我们证明X⊢D.DMtY，那么Xτ⊨Yτ，其中(·)τ,(·)τ:Stru→Fm。在第3节中我们已经证明，DMt相对于DMt框架是完全的，即A⊢DMtB，当且仅当，A⊨B。因此，如果A⊬DMtB，根据完全性有A⊭B，根据可靠性得A⊬D.DMtB，故从右向左方向成立，即D.DMt是DMt的保守扩张。

引理8A⊢A在D.DMt中可证。

证明：施归纳于公式A的复杂度。

(1)当A=p时，A⊢A是D.DMt的公理。

(2)当A=□B时，据归纳假设可得B⊢B，

(3)当A=■B时，证明方法与(2)类似；

(4)当A=A1∧A2时，据归纳假设可得A1⊢A1且A2⊢A2，

(5)当A=A1∨A2时，据归纳假设可得A1⊢A1且A2⊢A2，

命题3(A1)-(A16)，(R1)-(R7)在D.DMt中可证。

证明：仅举例说明：(A10)

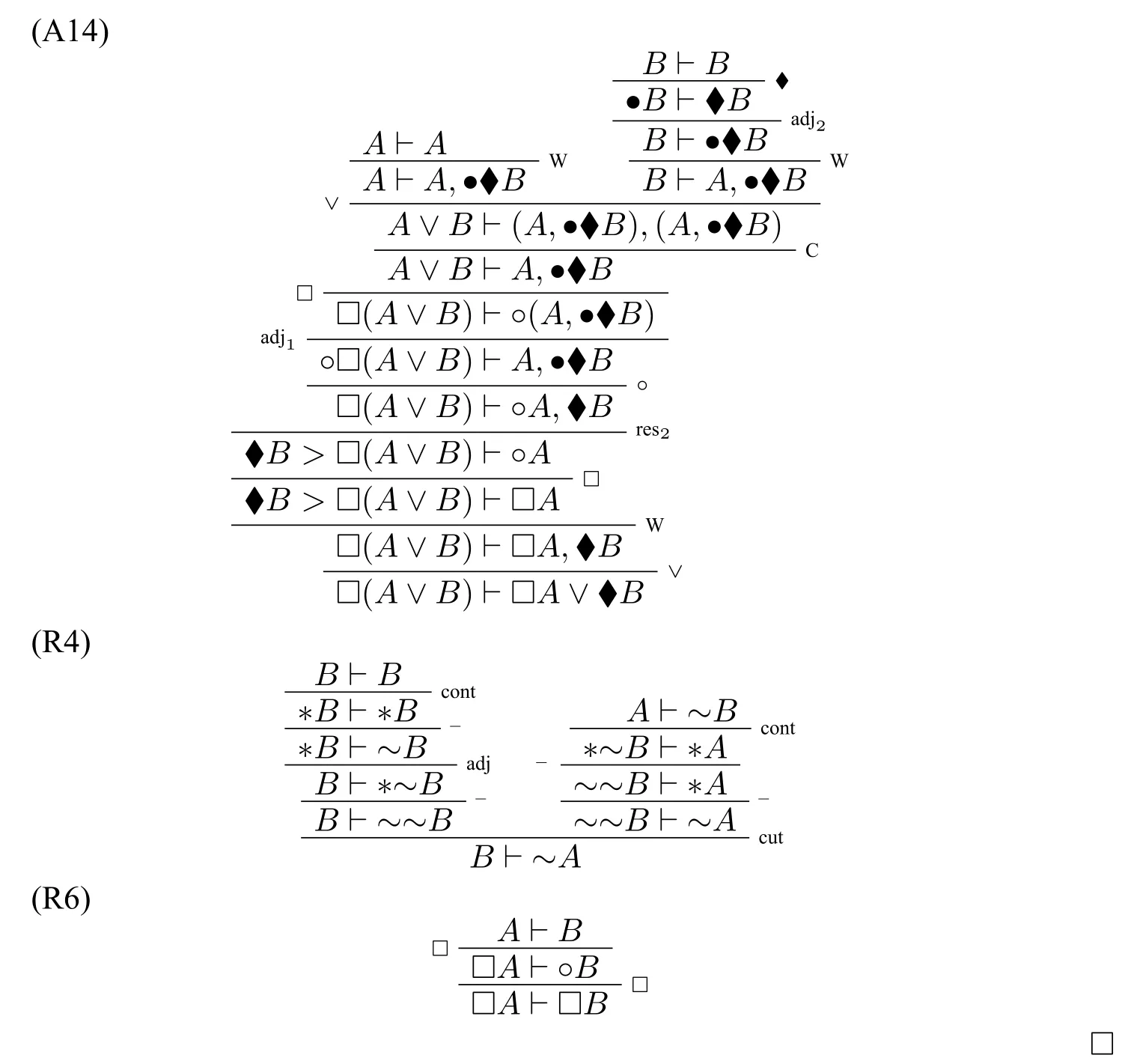
由引理7和命题3可得：

定理3任给A,B∈LDMt,如果A⊢DMtB，那么A⊢D.DMtB。

下面来证明从右向左方向。为了证明D.DMt的可靠性，我们首先给出D.DMt语言中新算子的满足关系。令M是一个时态德摩根模型，

·M,w⊨A.-B当且仅当存在w′∈W且w′≤w，w′⊭A且w′⊨B；

·M,w⊨A→B当且仅当对任意w≤w′∈W，w′⊭A或w′⊨B。

我们将X⊢Y解释为Xτ⊢Yτ，其递归定义如下：

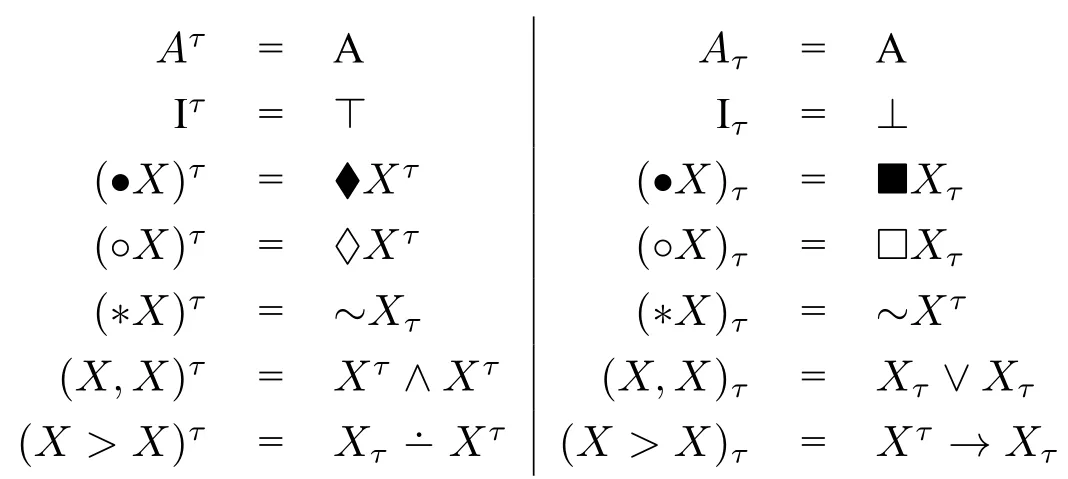
下证D.DMt的可靠性：

定理4如果X⊢Y在D.DMt中可证，那么Xτ⊨Yτ有效。

证明：只需证明D.DMt的公理和规则在时态德摩根框架上有效，这里仅举例说明。

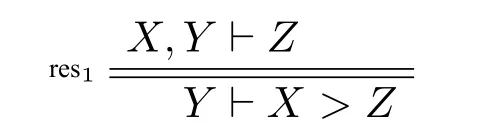
任给模型M，欲证：V′(Xτ∧Yτ)⊆V′(Zτ)，当且仅当，V′(Yτ)⊆V′(Xτ→Zτ)。

(⇒)假设V′(Yτ)⊈V′(Xτ→Zτ)，即存在w∈V′(Yτ)(i)且w/∈V′(Xτ→Zτ)。据满足关系得：存在w≤w′使得：w′∈V′(Xτ)(ii)且w′/∈V′(Zτ)。据题设条件，w′/∈V′(Xτ∧Yτ)，那么w′/∈V′(Xτ)或w′/∈V′(Yτ)(iii)。前者与(ii)矛盾。因为V′(Yτ)是上升集，据w≤w′与(i)，得w′∈V′(Yτ)，与(iii)矛盾。

(⇐)证明类似，从略。

任给模型M，欲证：V′(Xτ)⊆V′(Yτ∨Zτ)，当且仅当，V′(Yτ.-Xτ)⊆V′(Zτ)。

(⇒)假设V′(Yτ.-Xτ)⊈V′(Zτ)，即存在w∈V′(Yτ.-Xτ)且w/∈V′(Zτ)(i)。据满足关系得：存在w′≤w使得：w′/∈V′(Yτ)(ii)且w′∈V′(Xτ)。据题设条件，w′∈V′(Yτ∨Zτ)，那么w′∈V′(Yτ)或w′∈V′(Zτ)(iii)。前者与 (ii)矛盾。因为V′(Zτ)是上升集，据w′≤w与(i)，得w′/∈V′(Zτ)，与(iii)矛盾。(⇐)证明类似，从略。 □

故由定理2,4可得：

定理5任给A,B∈LDMt，如果A⊢D.DMtB，那么A⊢DMtB。

接下来我们证明D.DMt具有子公式性质，并且切割消除定理在D.DMt成立。如前所述，据[5]，如果系统满足(C1)，那么该系统满足子公式性质。如果系统满足(C1)-(C8)，该系统可证明切割消除。除(C8)外，其他性质均可根据系统规则形式确定。

下证D.DMt满足(C8)。

引理9D.DMt满足(C8)。

证明：施归纳于切割公式复杂度。

原子命题：

常项:

常项⊥的证明类似。

一元联结词:

■A,♦A,♢A的证明类似。

二元联结词:

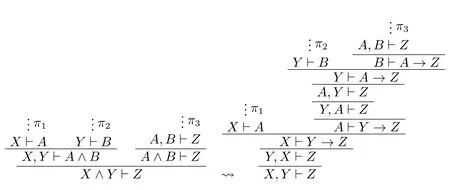
A∨B、A→B、A.-B证明类似。因此，如果规则(R)与规则(R’)的结论分别为:X⊢A，A⊢Y，其中A是两个规则的主要公式，且对这两个结论使用切割(Cut)规则得X⊢Y。那么X⊢Y要么与X⊢A或A⊢Y相同，要么可以对规则(R)与规则(R’)的前提使用切割规则，其中切割公式是A的真子公式，即(C8)成立。 □

定理6(切割消除，[5])如果X⊢Y在D.DMt中可证，那么X⊢Y的证明中不需要使用(Cut)。

证明：D.DMt满足(C2)-(C8)。 □

定理7(子公式性质，[5])如果X⊢Y在D.DMt中可证，那么其证明序列中出现的公式均为X,Y中的子公式。

证明：D.DMt满足(C1)。□

5 结论

本文从语义学及证明论的角度研究了时态德摩根逻辑，给出了时态德摩根逻辑的关系语义，证明了该逻辑的可靠性及完全性。本文还构建了时态德摩根逻辑的显示演算，同时证明了该演算具有切割消除定理和子公式性质。在此基础上，我们可以进一步推广[18]中的结论，在该文中克拉赫特用初始（primitive）公式的概念给出了时态逻辑Kt扩张显示化（displaying）的刻画条件，即:时态逻辑的扩张可被显示化，当且仅当，扩张的公理集为初始公式集（参见[18]，定理16）。我们可以用帕米迦娜与格里克等在[15]的定义55中提出的分析递归（analytic inductive）公式的概念得到时态德摩根逻辑的扩张显示化（displaying）的刻画条件，即扩张的公理集为分析递归（analytic inductive）公式集。除此之外，我们可以进一步研究不同的时态德摩根逻辑扩张，如：DM4t、DMS4t等，这有助于我们进一步地拓展非经典模态逻辑的视野及其应用。

[1]A.Anderson and N.Belnap,1975,Entailment:The Logic of Relevance and Necessity,Vol.1,Princeton and Oxford:Princeton University Press.

[2]O.Arieli and A.Avron,1996,“Reasoning with logical bilattices”,Journal of Logic,Language and Information,5:25-63.

[3]N.Belnap,1976,“How a computer should think”,in G.Ryle(ed.),Contemporary Aspects of Philosophy,pp.30-56,Boston:Oriel Press.

[4]N.Belnap,1977,“A useful four-valued logic”,Modern Uses of Multiple-valued Logic,pp.5-37,Netherlands:Springer.

[5]N.Belnap,1982,“Display logic”,Journal of Philosophical Logic,11(4):375-417.

[6]A.Bialynicki-Birula and H.Rasiowa,1957,“On the representation of quasi-Boolean algebras”,Bulletin of the Polish Academy of Science,5(3):259-261.

[7]K.BimboandM.Dunn,2001,“Four-valuedlogic”,NotreDameJournalofFormalLogic,42(3):171-192.

[8]M.Dunn,1966,The Algebra of Intensional Logics,PhD thesis,University of Pittsburgh.

[9]M.Dunn,1976,“Intuitive semantics for first-degree entailments and coupled trees”,Philosophical Studies,29:149-168.

[10]M.Dunn,1999,“A comparative study of various model-theoretic teartments of negation:A history of formal negation”,in D.Gabbay and H.Wansing(eds.),What is Negation?,pp.23-51,Dordrecht;Boston,Mass.:Kluwer Academic Publishers.

[11]A.V.Figallo and G.Pelaitay,2014,“Tense operators on De Morgan algebras”,Logic Journal of IGPL,22(2):255-267.

[12]R.Goré,1998,“Gaggles,GentzenandGalois:Howtodisplayyourfavouritesubstructurallogic”,Logic Journal of IGPL,6(5):669-694.

[13]R.Goré,1998,“Substructural logics on display”,Logic Journal of IGPL,6(3):451-504.

[14]G.Greco and A.Palmigiano,2016,“Linear logic properly displayed”,https://arxiv.org/abs/1611.04181.

[15]G.Greco,M.Ma,A.Palmigiano,A.Tzimoulis and Z.Zhao,2016,“Unified correspondence as a proof-theoretic tool”,Journal of Logic and Computation,exw022,http://dx.doi.org/10.1093/logcom/exw022.

[16]G.Greco and A.Palmigiano,2017,“Lattice logic properly displayed”,International Workshop on Logic,Language,Information,and Computation,pp.153-169.

[17]J.A.Kalman,1958,“Lattices with involution”,Transactions of the American Mathematical Society,87(2):485-491.

[18]M.Kracht,1996,“Power and weakness of the modal display calculus”,Proof Theory of Modal Logic,pp.93-121,Springer.

[19]G.Moisil,1935,“Recherches sur l’algebre de la logique”,Annales Scientifiques de l’Université de Jassy,22(3):1-117.

[20]H.Rasiowa,1974,An Algebraic Approach to Non-Classical Logics,Amsterdam:North-Holland Co.

[21]J.Spencer and N.Belnap,1966,“Intentionally complemented distributive lattices”,Portugalie Mathematics,25:99-104.

[22]H.Wansing,2013,Displaying Modal Logic,Springer Science Business Media.

[23]H.Wansing,2013,Proof theory of Modal Logic,Springer Science Business Media.