可快速编码的大围长QC-LDPC码构造方法
, ,,2
(1.重庆邮电大学 通信与信息工程学院 重庆高校市级光通信与网络重点实验室,重庆 400065;2.中国电子科技集团第四十四研究所,重庆 400065)
0 概述
由于具有逼近Shannon限的纠错性能[1],且译码复杂度较低,低密度奇偶校验(Low Density Parity Check,LDPC)码一直是近年来编码领域的研究热点,并被广泛应用在各类现代通信系统中。根据构造方法的不同,LDPC码[2]可分为随机码[3]和结构化码。随机LDPC码的编码复杂度与码长的平方成正比,且校验矩阵的硬件存储复杂度高,尤其在码长较长时不利于实际应用。因此,需要设计性能优越、校验矩阵具有一定结构特性的LDPC码。作为一种结构化的LDPC码,基于循环置换矩阵(Circulant Permutation Matrix,CPM)构造的准循环(Quasi Cyclic,QC)LDPC码[4-5]由于其简单灵活的设计方法引起了编码领域的广泛关注和研究。
虽然QC-LDPC码具有存储复杂度低、构造灵活简单等优点,然而传统QC-LDPC码的编码仍然需要通过校验矩阵转化成生成矩阵来实现,由于生成矩阵中子矩阵不一定具备稀疏的特性,因此在硬件编码实现时仍会占用大量存储空间。为了降低QC-LDPC码的编码复杂度,文献[6]提出了一种将校验矩阵的校验部分设计成近似下三角结构的构造方法,在编码过程中可直接通过校验矩阵进行迭代编码,从而有效地降低了编码复杂度。其中,IEEE 802.16e标准所采用的就是一种典型的采用准双对角线近似下三角结构的QC-LDPC码[7-8]。然而,其校验矩阵右半部分双对角线上的子矩阵均是单位阵,这些确定性单位阵的存在不仅破坏了这类QC-LDPC码的随机性,使得码字性能有一定的损失,而且导致一些基于组合设计、代数设计等确定性方法构造大围长QC-LDPC码存在局限性。
针对上述问题,本文提出一种基于独立行列映射序列(Independent Row-column Mapping Sequence,IRCMS)算法以及通过CPM的行列循环移位和掩码技术来构造围长为8、可快速编码的QC-LDPC码的方法。该方法采用IRCMS算法构造围长为8的全局校验矩阵,然后通过CPM的行列循环移位使得校验部分的矩阵具有一定的半随机结构特性,最后利用掩码技术得到一种改进型的半随机准双对角线结构及可快速编码的大围长QC-LDPC码。
1 大围长QC-LDPC码
基于CPM构造的规则(J,L)QC-LDPC码,列重为J,行重为L,其校验矩阵可表示如下[9]:
(1)
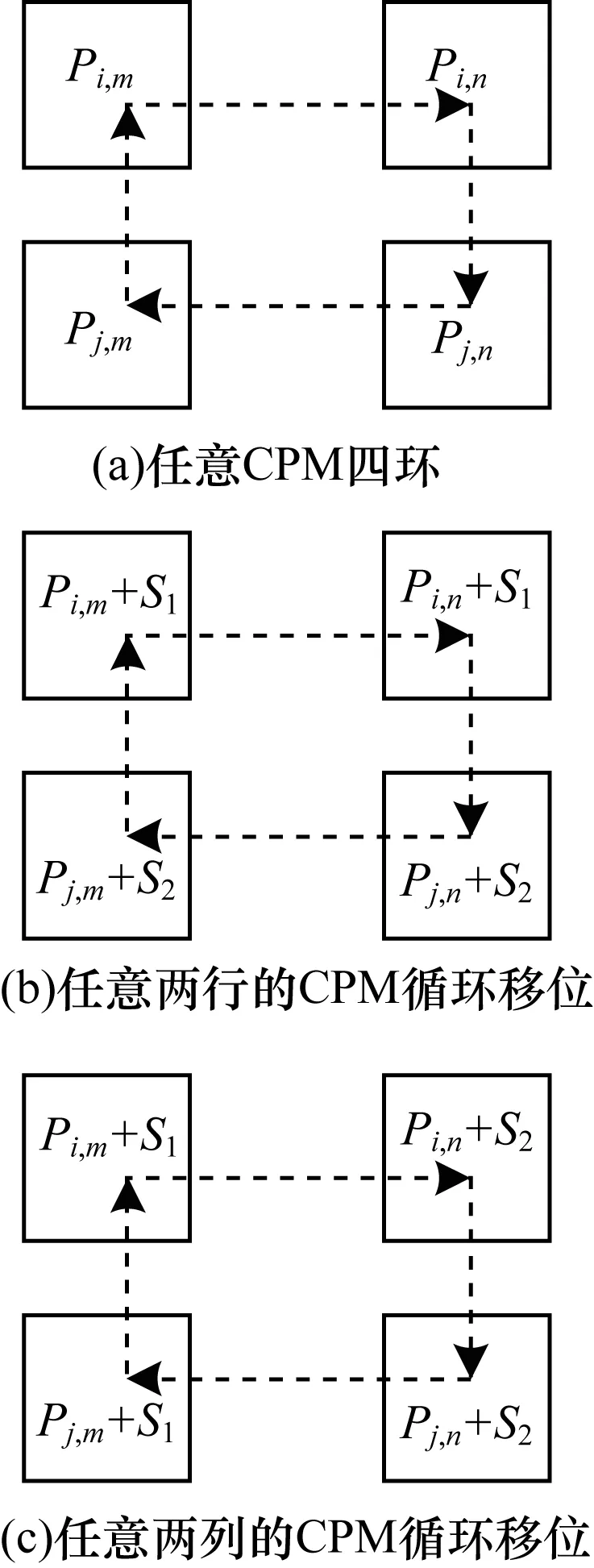
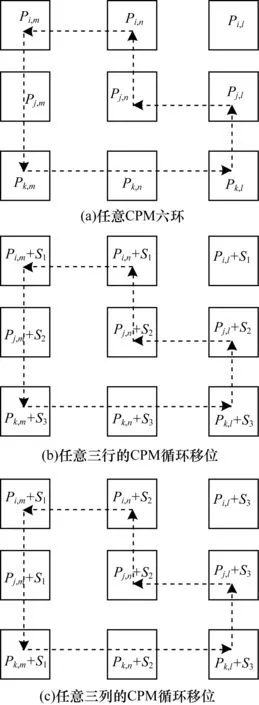
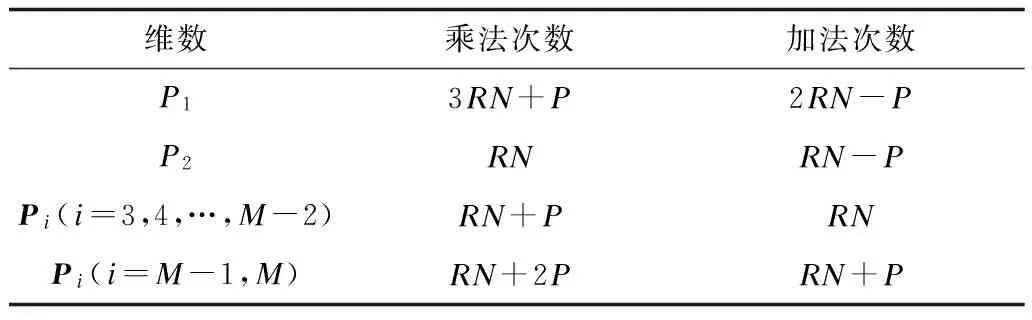
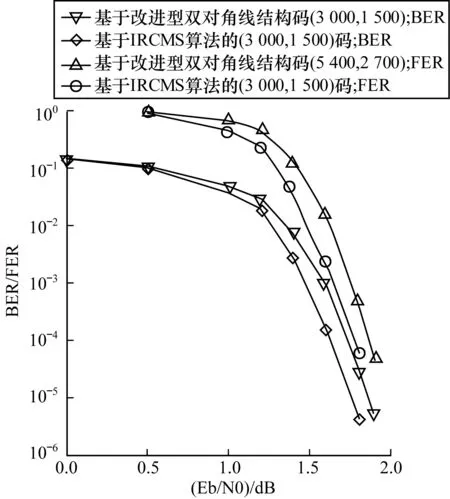
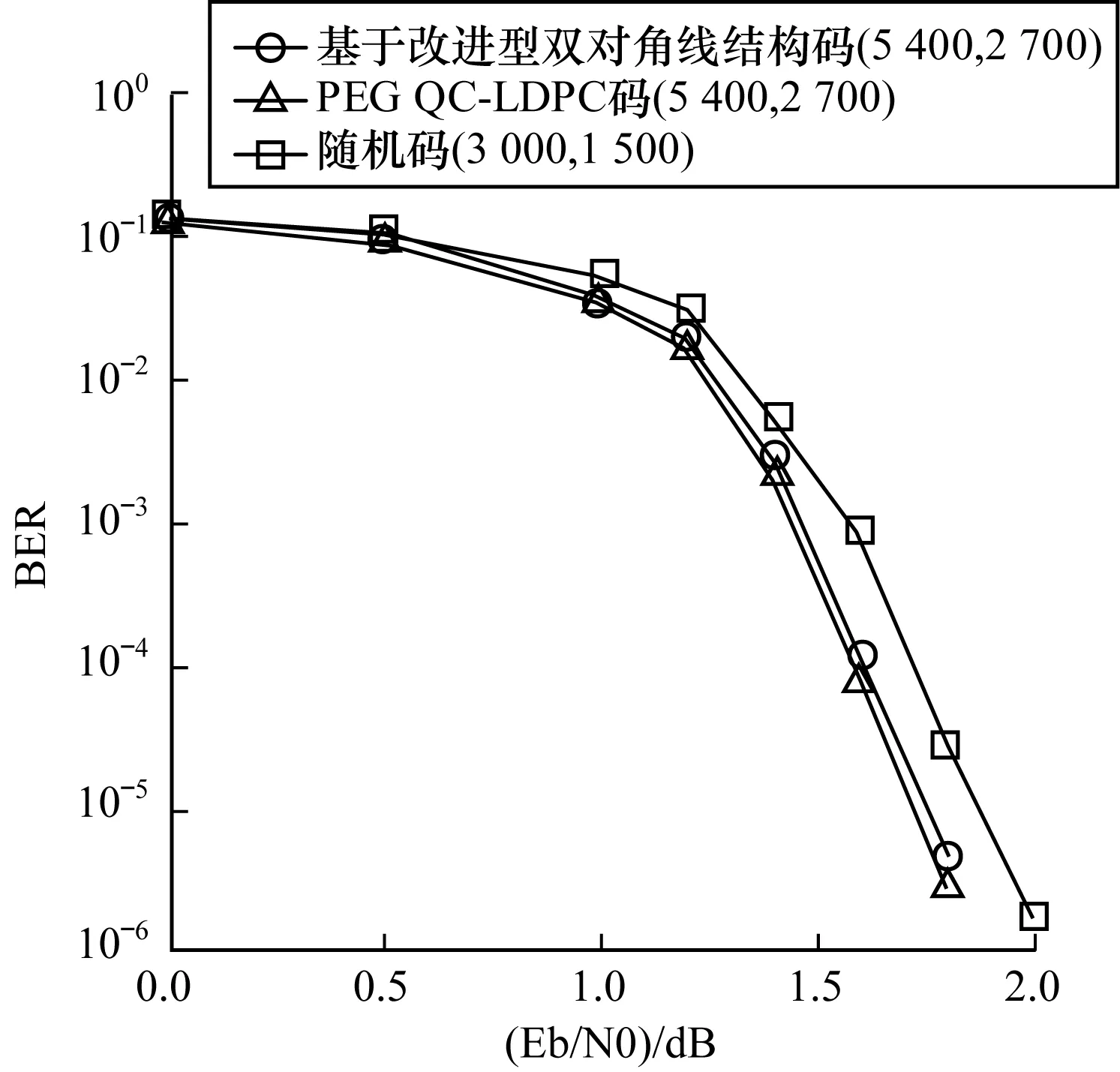
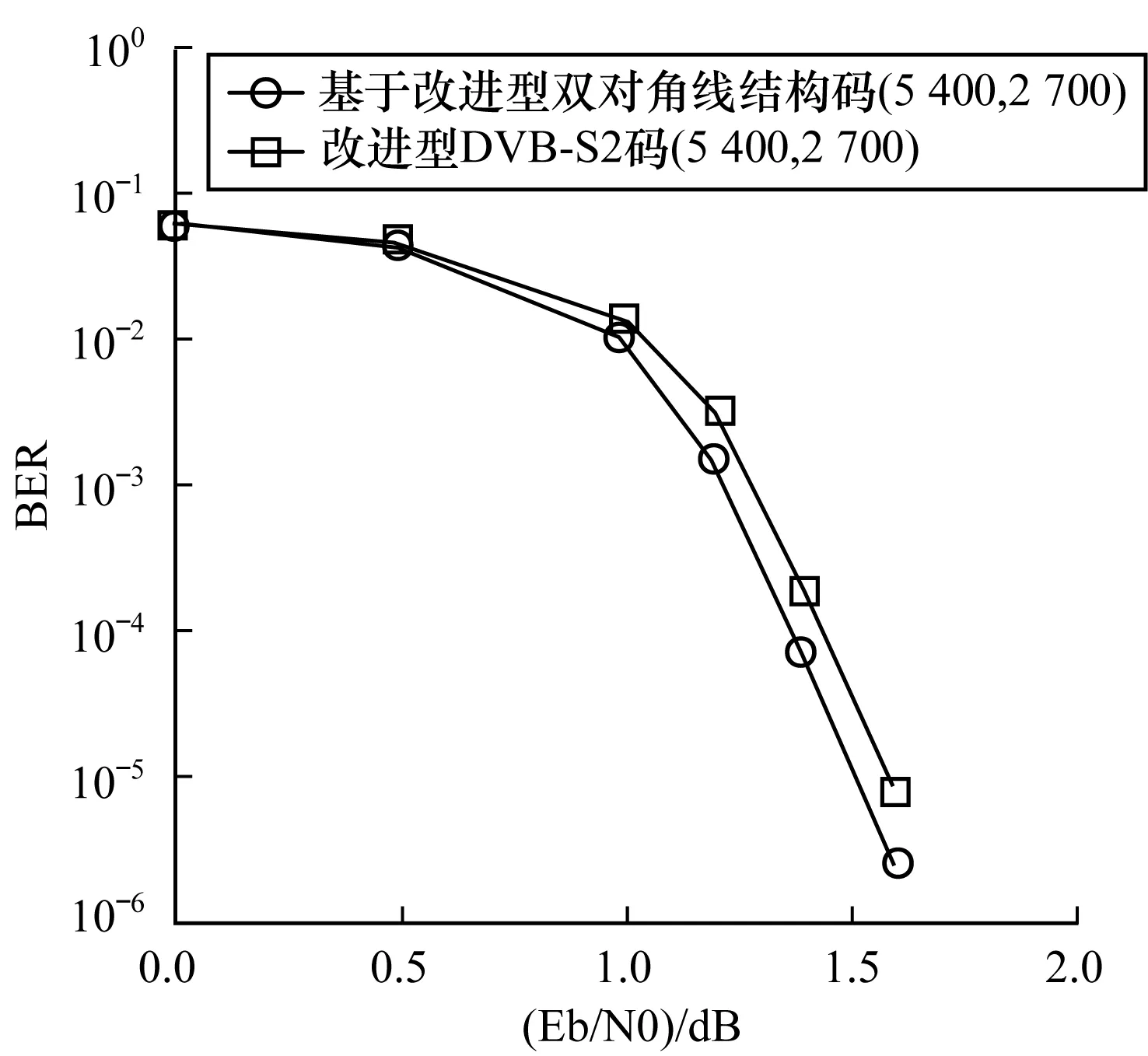
其中,1≤j≤J,1≤l≤L,0≤Pj,l (2) 根据IRCMS算法[10],Pr,c=f(r,c)=g(r)h(c),其中,g(r)(r=1,2,…,J)和h(c)(c=1,2,…,L)分别为互异的非负整数序列。当预先设定的序列h(c)已知时,只需要根据IRCMS算法搜索序列g(r),并且确定P的取值范围,即可使得所构造校验矩阵对应Tanner图[11]的围长至少为8。 IRCMS算法的步骤如下: 输入列重J和序列h={h1,h2,…,hL} 输出序列g={g1,g2,…,gJ} 初始化g初始化为{0,1},令j=0。 步骤1如果j<(J-2),则转至步骤2;否则结束,搜索完成。 步骤2令Y=t+1(t等于当前g中最后一个元素的值)。 步骤3在当前集合g中遍历地选取任意2个不相同数g(i)和g(j),如果对于当前h中任意3个{hl,hm,hn}∈h都满足: (Y-g(i))(hn-hl)=(g(j)-g(i))(hm-hl) (3) 那么设置flag=1;否则,设置flag=0。 步骤4如果flag=1,令Y=Y+1,返回至步骤3;如果flag=0,令g=g∪Y,j=j+1,返回至步骤1。 由上可知,指数矩阵E可以由IRCMS算法所确定,根据文献[12]中的定理1可知,当循环置换矩阵的维数P满足:P>gmaxhmax时,所构造的QC-LDPC码对应Tanner图的围长至少为8。 本节给出一种可快速编码的大围长QC-LDPC码构造方法。该方法首先基于IRCMS算法构造围长为8的全局校验矩阵,然后采用CPM的行列循环移位使得校验部分的子矩阵排列满足一定的结构特性,最后对所得矩阵进行掩码处理得到具有改进型准双对角线结构的校验矩阵。 1)基于IRCMS算法构造围长为8的初始校验矩阵,并且将全局校验矩阵分成如下部分: (4) 其中,Hk由P×P维CPM的行列循环移位构成的M×(N-M)矩阵阵列,对应于校验矩阵H的信息位部分,Hp是由P×P的CPM构成M×M的矩阵阵列,对应于校验矩阵H的校验位部分。 本文所提出的改进型双对角结构Hp矩阵如下: (5) 其中,hi,j表示校验部分矩阵Hp的第i行、第j列的子矩阵,当0 2)对H矩阵的最后三行的CPM向右循环移位。其中,Sr(i)表示对第i行的CPM同时向右循环移位Sr(i)位,i=M-2,M-1,M: (6) 然后,对Hp矩阵第2列至第M-2列的CPM分别同时向左循环移位。其中,Sc(i)表示对Hp矩阵的第i列CPM同时向左循环移Sc(i)位,i=2,3,…,M-2: Sc(i)=Ep(i-1,i) (7) 定理1基矩阵E中存在序列(p1,p2,…,p2l),其中任意两相邻元素pi和pi+1(包括p1和p2l)位于同一行或者同一列,不相邻元素位于不同行且不同列,则该序列构成长度为2l的环的充分必要条件为[12]: (8) 引理1如果基于CPM构造的QC-LDPC码没有四环、六环存在,则对其校验矩阵的若干行或列的CPM分别同时循环移位,若同行或者同列的CPM移位位数相同,该矩阵无四环、六环产生。 证明: 1) 若基于CPM构造的QC-LDPC码的校验矩阵无四环,根据定理1,对如图1(a)所示的任意的两行(i,j)、两列(m,n),有: Pi,m-Pi,n+Pj,n-Pj,m≠0(modP) (9) 对其校验矩阵的若干行或列的CPM分别同时向左或向右循环移位。首先,对如图1(a)所示的两行CPM分别同时进行循环移S1、S2位,则如图1(b)所示的四环存在充要条件为: (Pi,m+S1)-(Pi,n+S1)+(Pj,n+S2)- (Pj,m+S2)=0(modP) (10) 即: Pi,m-Pi,n+Pj,m-Pj,n=0(modP) (11) 但上式与式(9)矛盾,故四环存在条件不满足,即该校验矩阵没有四环的存在。同理,对如图1(a)所示的两列CPM分别同时进行循环移S1、S2位,则图1(c)所示的四环存在条件亦不满足。故对校验矩阵的若干行或列CPM同时进行循环移位,若同行或者同列的CPM移位位数相同,不会产生四环。 图1 四环的不存在性示意图 2) 若基于CPM构造的QC-LDPC码的校验矩阵无六环,则根据定理1,对图2(a)所示的任意的三行(i,j,k)、两列(m,n,l),有: Pi,m-Pi,n+Pj,n-Pj,l+Pk,l-Pk,m≠0(modP) (12) 对校验矩阵若干行或列的CPM分别同时进行循环移位,对如图2(a)所示的三行CPM同时循环移S1、S2、S3位后,如图2(b)所示的六环存在充要条件为: (Pi,m+S1)-(Pi,n+S1)+(Pj,n+S2)- (Pj,l+S2)+(Pk,l+S3)-(Pk,m+S3)= 0(modP) (13) 即: Pi,m-Pi,n+Pj,n-Pj,l+Pk,l-Pk,m=0(modP) (14) 但上式与式(12)矛盾,故六环存在条件不满足,则校验矩阵没有六环。同理,对如图2(a)所示的三列CPM分别同时进行循环移S1、S2、S3位,则如图2(c)所示的六环存在条件亦不满足。故校验矩阵的若干行或列的CPM分别同时进行循环移位后,若同行或者同列的CPM移位位数相同,无六环产生。引理1证毕。 图2 六环的不存在性示意图 由引理1可知,上述行列循环移位操作不会使得校验矩阵产生四环、六环,即不改变所构造的全局校验矩阵的四环、六环特性。 3)对经过行列循环移位后的H矩阵进行掩码处理。掩码技术通常被简单地用来采用一些全零矩阵替换相应位置P×P的CPM。对于一个由P×P的CPM所构成的M×N矩阵阵列H而言,设M(M,N)=(mj,l)0≤j M⊗H=(mj,l·Hj,l)0≤j (15) 如果mj,l=1,则mi,j·Hi,j=I(Pi,j);否则mj,l·Hj,l为P×P的I(-1)矩阵,即P×P的零矩阵。 为了使得最终所构造的校验矩阵右半部分满足式(5)所示结构,则M矩阵对应于Hp部分的Mp如下: (16) QC-LDPC码校验矩阵的较优行重分布为近似相等的二三个连续行重值[13]。由于Mp的行重为近似相等的2个值,因此为了在得到一个稀疏矩阵H的同时,优化码字的度分布,则掩码矩阵M的左半部分Mk的行重也需近似相等,从而使得所构造校验矩阵H的行重为近似相等的二三个数值。 由于基于IRCMS算法构造围长为8的H矩阵没有四环、六环,因此经过掩码处理后的H亦不会有四环、六环[14]。所以,本文基于IRCMS算法、行列循环置换和掩码技术构造的可快速编码QC-LDPC码字保持了大围长特性。 C=[S,P] (17) 由于编码向量C为校验矩阵H的零空间,则在GF(2)域中可得: (18) 根据式(5)的前M-3行结构,首先依次迭代至式(18)的第1行到第M-3行: (19) 则可得校验位向量Pi(i=2,3,…,M-2): (20) 然后,迭代至式(18)的第M-2行至第M行: (21) 将式(21)中3个等式相加,可得: (22) 将式(22)代入到式(21)中,即可得: (23) 编码复杂度主要关注编码过程的运算量、运算复杂度和编码所需存储的参数,运算量即乘法和加法次数,运算复杂度即运算量与码长的变化关系。QC-LDPC码的各个子矩阵都是稀疏矩阵,因此按照稀疏矩阵的运算方式可大大减小运算量。计算式(22)、式(23)中Pi的运算量如表1所示。 表1 编码算法的运算量 在表1中,R表示码率,N表示扩展之后的码长,N=n×p,P表示校验矩阵中CPM的维数。 从表 1 可明显地看到,计算各个校验分向量Pi的运算复杂度为O(N),即运算复杂度与码长呈线性关系。因此,本节基于改进型准双对角结构构造的可快速编码QC-LDPC码具有完全线性的编码复杂度,编码效率很高。 本节通过仿真将本文构造的围长为8、可快速编码的QC-LDPC码,与采用IRCMS算法构造围长为8的规则QC-LDPC码、基于PEG算法构造的QC-LDPC码[15-16]和基于改进型DVB-S2码[17]的性能分别做比较。仿真是在加性高斯白噪声(Additive White GaussNoise,AWGN)信道下进行,采用二进制相移键控(Binary Phase Shift Keying,BPSK)方式进行调制,采用置信传播(Belief Propagation,BP)算法进行译码,设置最大迭代次等于100。 首先,设置h={0,1,2,3,4,6,7,8,9,10},J=5。根据IRCMS算法,产生序列g={0,1,11,12,25}。由P>gmaxhmax取P=300。然后,根据式(6)和式(7)对所构造的H矩阵进行CPM的行列循环移位。最后,对CPM行列循环移位后的矩阵进行掩码处理。所采用的掩码矩阵如下: (24) 1)当设置P=300时,由上述指数矩阵E=[Ek,Ep]可构造围长为8、可快速编码的(3 000,1 500)QC-LDPC码。本文构造的不规则(3 000,1 500)QC-LDPC码与文献[15]中基于IRCMS算法构造围长为8的(3 000,1 500)规则QC-LDPC码的误码率(Bit Error Rate,BER)和误帧率(Frame Error Rate,FER)性能对比如图3所示。 图3本文所构造的码字与采用IRCMS算法构造的规则QC-LDPC码的BER和FER性能对比 由图3可知,本文构造的可快速编码QC-LDPC码译码的性能明显优于基于IRCMS算法构造的围长为8的规则QC-LDPC码,在BER为10-5时,在编码复杂度更低的基础上,有0.15 dB左右的编码增益。 将本文所构造的不规则(3 000,1 500)QC-LDPC码与基于PEG算法构造的相同码长、码率、度分布的不规则QC-LDPC码和围长为6的随机QC-LDPC码进行比较。由图4可知,本文所构造的码字与基于PEG算法构造的不规则QC-LDPC码性能相当,且本文所构造的码字具有完全线性的编码复杂度,编码复杂度更低。与围长为6的随机QC-LDPC码相比,本文所构造的码字具有更加优越的性能,在误码率达到10-5时,码字性能有0.2 dB的提升。 图4本文所构造的码字与基于PEG算法构造的QC-LDPC码和随机QC-LDPC码的BER性能对比 2)当设置P=540时,可构造围长为8、可快速编码的(5 400,2 700)QC-LDPC码,将这种码字与文献[17]中改进型DVB-S2码相比,其仿真结果如图5所示。 图5本文所构造的码字与改进型DVB-S2码字的BER性能对比 由图5可知,与文献[17]中改进型的DVB-S2码相比,本文所构造的可快速编码的QC-LDPC码不仅同样具有可快速编码特性,而且性能有了一定的提升,在误码率达到10-5时,其码字性能提高了0.1 dB左右。 本文基于IRCMS算法、CPM的行列循环移位以及掩码技术提出一种围长为8、可快速编码的QC-LDPC码构造方法。该方法所构造的QC-LDPC码不仅保持了围长至少为8的特性,而且还可以利用该改进型准双对角线结构的校验矩阵直接进行简单快速的编码,在保证优异性能的同时,降低了QC-LDPC码的编码复杂度。仿真结果表明,本文所构造的码字不仅具有线性的编码复杂度,而且性能较优。与已有的确定性构造方法相比,该方法是一种基于计算机搜索的构造方法,虽然比较灵活,但为满足各种约束条件,没有解决码的存在性问题,存在构造失败的可能性,下一步将针对上述问题进行改进。 [1] MACKAY D J C,NEAL R M.Near Shannon Limit Performance of Low Density Parity Check Codes[J].Electronics Letters,1996,32(18):1645-1646. [2] GALLAGER R G.Low-density Parity-check Codes[J].IRE Transactions on Information Theory,1962,8(1):21-28. [3] MACKAY D J C.Good Error-correcting Codes Based on Very Sparse Matrices[J].IEEE Transactions on Information Theory,1999,45(2):399-431. [4] FOSSORIER M P C.Quasi-cyclic Low-density Parity-check Codes from Circulant Permutation Matrices[J].IEEE Transactions on Information Theory,2004,50(8):1788-1793. [5] 焦新泉,陈建军,单彦虎.基于 BIBD 和循环置换矩阵的 LDPC码[J].计算机工程,2012,38(2):282-283. [6] MYUNG S,YANG K,KIM J.Quasi-cyclic LDPC Codes for Fast Encoding[J].IEEE Transactions on Information Theory,2005,51(8):2894-2901. [7] WANG H,CHEN S,ZHU C,et al.A Novel QC-LDPC Code with Flexible Construction and Low Error Floor[C]//Proceedings of the 16th International Conference on Advanced Communication Technology.Washington D.C.,USA:IEEE Press,2014:431-436. [8] IEEE.Part 16:Air Interface for Fixed and Mobile Broadband Wireless Access Systems[S].New York,USA:Institute of Electrical and Electronics Engineering,2006. [9] WANG R,LI Y,ZHAO H,et al.Construction of Girth-eight Quasi-cyclic Low-density Parity-check Codes with Low Encoding Complexity[J].IET Communications,2016,10(2):148-153. [10] WANG L,ZHANG X,YU F,et al.QC-LDPC Codes with Girth Eight Based on Independent Row-column Mapping Sequence[J].IEEE Communications Letters,2013,17(11):2140-2143. [11] TANNER R M.A Recursive Approach to Low Complexity Codes[J].IEEE Transactions on Information Theory,1981,27(5):533-547. [12] 彭 立,朱光喜.QC-LDPC 码的置换矩阵循环移位次数设计[J].电子学报,2010,38(4):786-790. [13] KANG J,HUANG Q,ZHANG L,et al.Quasi-cyclic LDPC Codes:An Algebraic Construction[J].IEEE Transactions on Communications,2010,58(5):1383-1396. [14] KAMIYA N.Efficiently Encodable Irregular QC-LDPC Codes Constructed from Self-reciprocal Generator Polynomials of MDS Codes[J].IEEE Communications Letters,2010,14(9):1-3. [15] LI Z,KUMAR K V.A Class of Good Quasi-cyclic Low-density Parity Checks Code Based on Progressive Edge Growth Graph [C]//Proceedings of Conference on Signals,Systems & Computers.Washington D.C.,USA:IEEE Press,2004:1990-1994. [16] JIANG X,XIA X G,LEE M H.Efficient Progressive Edge-growth Algorithm Based on Chinese Remainder Theorem[J].IEEE Transactions on Communications,2014,62(2):442-451. [17] 肖 扬,范 俊,黄 希.DVB-S2标准的LDPC码改进[J].铁道学报,2011,33(2):52-59.2 可快速编码的大围长QC-LDPC码设计
2.1 校验矩阵的构造方法

2.2 快速编码算法与编码复杂度分析
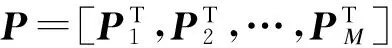
3 性能仿真与分析
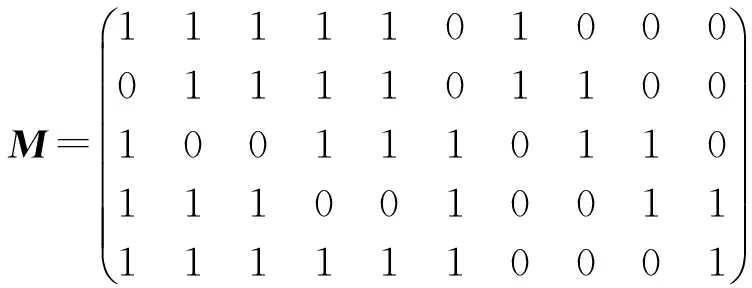
4 结束语

