不同温度下无后坐炮内弹道过程多维随机变量数值模拟
李春雷,王雨时,张志彪
(南京理工大学 机械工程学院,江苏 南京 210094)
无后坐炮内弹道过程中随机影响因素很多。由于内弹道整个过程只持续很短的时间,所以很多影响无后坐炮内弹道过程的随机变量无法通过实验获知。
为了得到内弹道影响因素的随机分布,文献[1]基于经典内弹道学模型,采用蒙特卡罗方法模拟了内弹道过程中初始参量随机性导致的最大膛压和初速的随机波动现象,得到某高射炮的最大膛压和初速的随机分布特性。其中初始参量变化只考虑了药量、药厚和火药力,并未综合考虑弹丸发射中其他初始参量,例如弹质量和药室容积。文献[2]基于内弹道势平衡理论研究了不同火药静态燃烧规律与初速或然误差之间的内在联系,利用建立的初速或然误差的随机模拟理论,得到了应用密闭爆发器来预估初速或然误差的工程方法。文献[3]在考虑火药随机燃烧基础上,利用火炮内弹道一维两相流模型,随机模拟了点火管因随机破孔而对弹道性能造成的影响;从概率统计的角度对点火管破孔、最大膛压以及最大负压差进行了统计分析,统计分析结果基本能反映出膛内射击过程的某些内在统计规律。文献[4]对无后坐炮整个身管和出炮口一定距离的流场进行了数值模拟,得到的流场结果符合预期。文献[5]为了实现无后坐炮在有限空间内的安全发射,设计了一种含液态平衡体的新型装药结构,并进行了某口径无后坐炮内弹道性能试验,建立了相应的内弹道模型,计算结果与试验结果吻合较好。在此基础上,分析了液态平衡体初始质量、密度、火药弧厚、喷管喉部直径以及挤进压力等参数对内弹道性能的影响。
综上所述,蒙特卡洛方法解决了在实际中不可能在相同条件下做大量试验的突出问题,是深入系统了解问题分布的有效方法。因此,为了精确设计身管强度、弹体强度和精确分析引信解除保险性能,在考虑药厚、火药力、药量、药室容积和弹丸质量随机性基础上,应用蒙特卡洛方法和无后坐炮经典内弹道模型,随机模拟了不同随机因素对弹道性能的影响。本文在不同温度下同时考虑药厚、火药力、药量、药室容积和弹丸质量随机性,得到了上述初始参量随机影响因素下的某无后坐炮内弹道膛压曲线包络线,该解算结果能较好地反映出膛内射击过程的变化规律,可用于精细设计身管强度、弹体强度和精确分析引信解除保险性能。
1 随机模拟方法与无后坐炮内弹道
1.1 随机模拟方法与无后坐炮内弹道的特点
随机模拟方法又称蒙特卡罗(Monte Carlo)方法,是一种通过设定随机过程,反复生成时间序列,计算参数估计量或统计量,进而研究其分布特征的方法。其详细定义见文献[6-7]。
与一般火炮相比,无后坐炮在射击过程中有大量火药气体从喷管中流出。因气体流出影响的内弹道性能参数分别有流量qm、总量Qm和推力F。在一维等熵条件下,有:
(1)
(2)
F=CFSjp
(3)
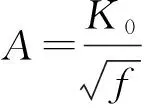
无后坐炮内弹道方程组由1个代数方程和6个一阶微分方程组成。在此只需得到膛压曲线,因此方程组中关于速度的方程可不予考虑。并且一般情况下,该方程组不存在解析解,因此,通常采用数值方法求解。
为了便于Matlab软件编制,将其化为无量纲的微分方程组形式,具体形式详见文献[8]。对其采用Matlab软件自身提供的求常微分方程数值解的四阶、五阶的ode45函数求解。
1.2 仿真可信性说明
根据文献[9]提供的1965年式82 mm无后坐炮的内弹道初始数据,利用编写好的程序对其内弹道进行仿真,结果如表1所示,表中,l为弹丸行程,p为膛压,ε为仿真结果与文献[9]中结果之间的相对误差。
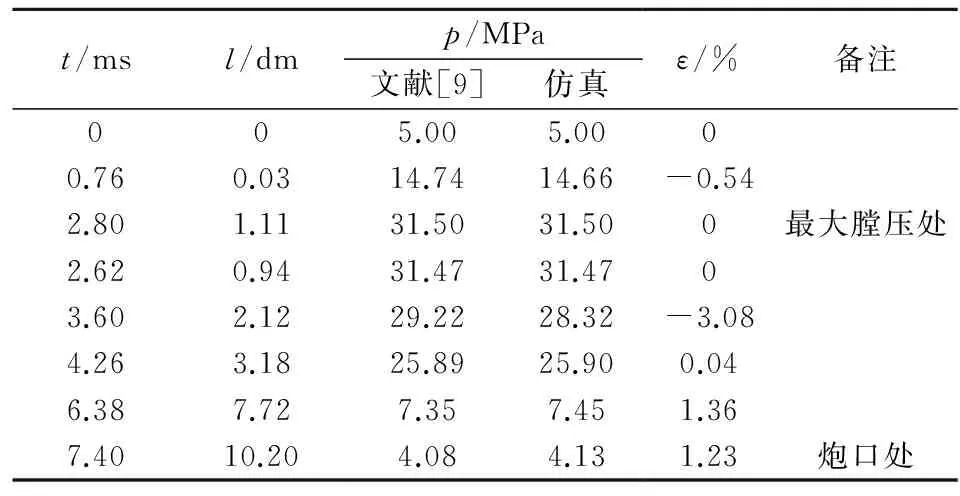
表1 常温下(15 ℃)1965式82 mm无后坐炮身管内弹道仿真结果
由表1可知,上述内弹道膛压解算结果与文献[9]计算得到的内弹道膛压结算结果相对误差很小,因此本文所用的内弹道仿真模型、软件和解算结果是可信的。
2 内弹道膛压随机模拟
2.1 弹质量随机模拟
首先假设无后坐炮药室容积、发射药药量、发射药药厚和发射药火药力恒定不变,环境温度即药温为常温(15 ℃)。根据文献[10],弹质量随机变化,服从正态分布。由文献[11],1个计算组内不同弹质量偏差一般不超过1个弹质量分级符号。根据文献[12],一般榴弹的弹质量符号在4个以内,故在此取4个适中符号,其中弹质量符号和适中符号的具体定义见文献[12];中间误差[13]Em代表随机变量出现在均值左右Em范围内的概率为50%,在均值左右4Em范围内随机变量出现的概率近似为1;由此即可估算出弹丸质量分布的标准差σmp=0.009 884mp,其中,mp为弹丸质量。
由Monte-Carlo方法产生5个弹质量随机值,然后循环模拟内弹道过程5次,得到的膛压曲线如图1所示。
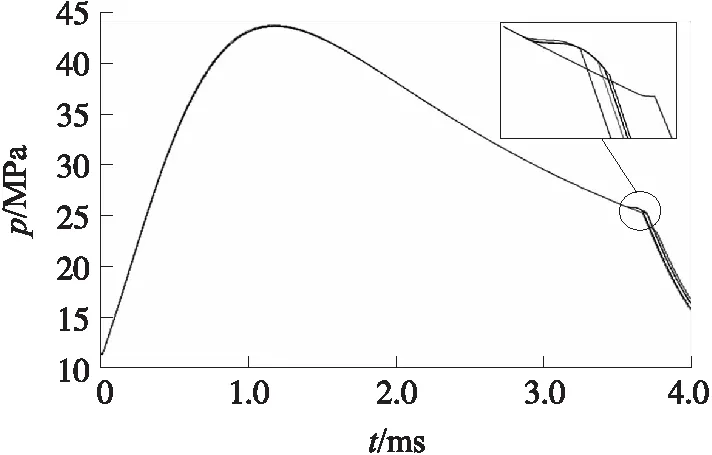
图1 随机模拟弹质量获得的膛压曲线
从图1知,在5次随机模拟后,图示局部放大区域曲线有交叉,因此随机模拟弹质量所得到的膛压曲线包络线不是弹质量中最大与最小所对应的膛压曲线。进一步由Monte-Carlo方法产生105个弹质量随机值,然后循环模拟内弹道过程105次,通过比较某时间(某行程)对应的压力值,得到105条膛压曲线的包络线,如图2所示。
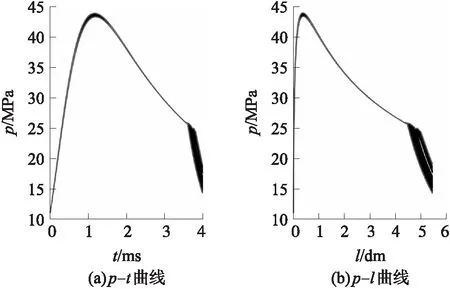
图2 随机模拟弹质量对某无后坐炮内弹道膛压曲线分布区域的影响
图2中,最大膛压附近的膛压跳动最大值为0.775 3 MPa,炮口附近的膛压跳动最大值为5.526 3 MPa。
2.2 发射药药厚随机模拟
首先假设无后坐炮药室容积、弹质量、发射药药量和发射药火药力是恒定不变的,环境温度即药温为常温(15 ℃)。再假设发射药药厚随机变化,服从正态分布。由文献[14],全弹装配时,所有尺寸均符合正态分布,其散布中心即为公差带中心,散布范围6σe即为公差带宽度W。由于正态分布只有99.73%的取值在公差带宽度W内,故要剔除在公差带W之外的抽样尺寸即不合格的尺寸。根据文献[15],某无后坐炮发射药药厚制造公差带宽度为0.16 mm,因此可估算出发射药药厚的标准差σe约为(0.16/6) mm=0.026 67 mm。
利用2.1的方法可知,随机模拟药厚所得到的膛压曲线包络线也并不是一组随机发射药药厚数值中最大与最小所对应的膛压曲线。进一步由Monte-Carlo方法产生105个发射药药厚随机值,然后循环模拟内弹道过程105次,通过比较某时间(某行程)对应的压力值,得到105条膛压曲线的包络线,如图3所示。
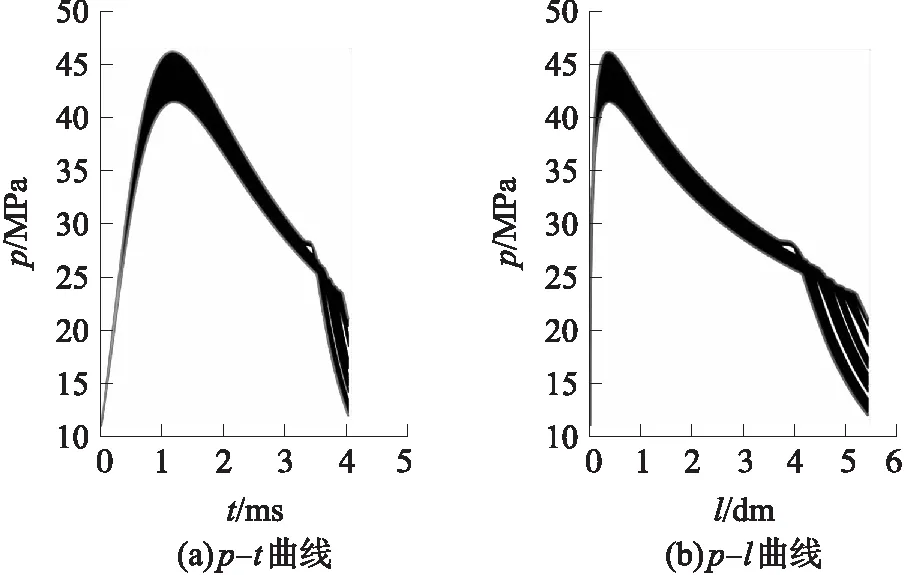
图3 发射药药厚随机值对某无后坐炮内弹道膛压曲线分布区域的影响
图3中,最大膛压附近的膛压跳动最大值为5.247 3 MPa,炮口附近的膛压跳动最大值为10.785 1 MPa。
2.3 发射药药量随机模拟
首先假设无后坐炮药室容积、弹质量、发射药药厚和发射药火药力恒定不变,环境温度即药温为常温(15 ℃),发射药药量随机变化,服从正态分布。全弹装配时,100 mm和105 mm口径弹的发射药药量公差为±(4~6)g,由天平精度保证,因此某无后坐炮的发射药药量公差估取为±(1~3) g,则发射药药量标准差σmw分别取为0.33 g,0.67 g,1 g。
利用2.1的方法可知,随机模拟发射药药量所得到的膛压曲线包络线并不是一组随机发射药药量中最大与最小所对应的膛压曲线。进一步由Monte-Carlo方法产生105个发射药药量随机值,然后循环模拟内弹道过程105次,通过比较某时间(某行程)对应的压力值,得到105条膛压曲线的包络线。发射药药量标准差为0.33 g,0.67 g,1 g,所对应的包络线如图4~图6所示。
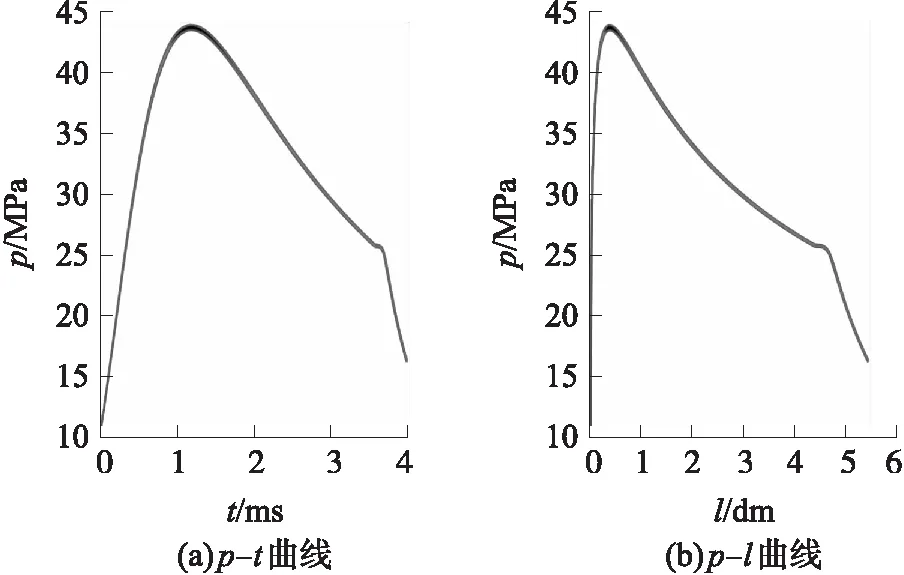
图4 发射药药量标准差σmw=0.33 g时随机发射药药量对某无后坐炮内弹道膛压曲线分布区域的影响
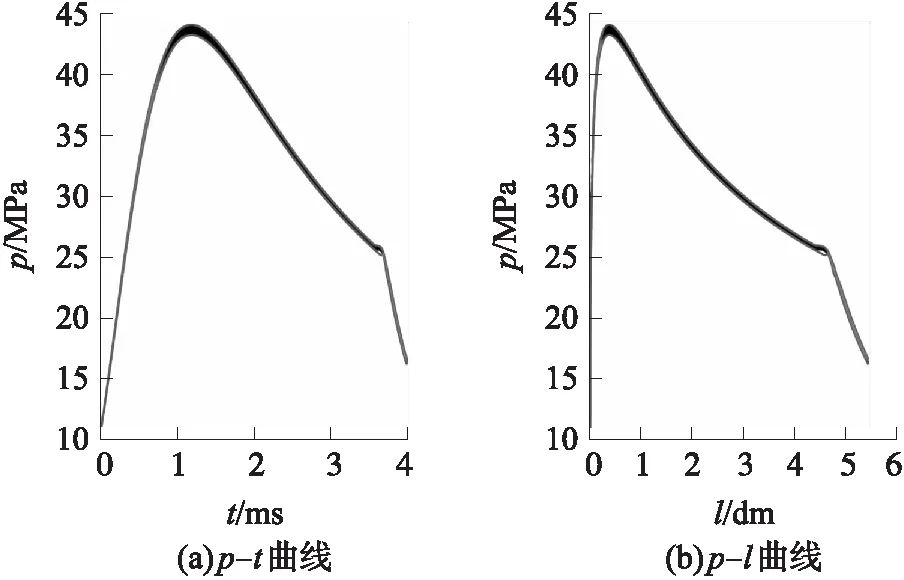
图5 发射药药量标准差σmw=0.67 g时随机发射药药量对某无后坐炮内弹道膛压曲线分布区域的影响
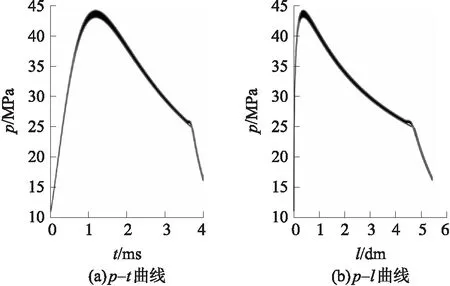
图6 发射药药量标准差σmw=1 g时随机发射药药量对某无后坐炮内弹道膛压曲线分布区域的影响
由图4~图6可知,最大膛压附近的膛压跳动最大值和炮口附近的膛压跳动最大值,在σmw=0.33 g时分别为0.429 7 MPa,0.143 4 MPa;在σmw=0.67 g时分别为0.841 4 MPa,0.441 7 MPa;在σmw=1 g时分别为1.255 7 MPa,0.523 6 MPa。
2.4 发射药火药力随机模拟
首先假设无后坐炮发射药药厚、弹质量、发射药药量和药室容积恒定不变,环境温度即药温为常温(15 ℃),发射药火药力随机变化,服从正态分布。据靶场统计可知,一批发射药的火药力的变动范围在±3%以内,因此可估计发射药火药力的标准差σf=1%。
利用2.1的方法可知,随机模拟火药力所得到的膛压曲线包络线并不是一组随机火药力中最大与最小所对应的膛压曲线。进一步由Monte-Carlo方法产生105个发射药火药力随机值,然后循环模拟内弹道过程105次,通过比较某时间(某行程)对应的压力值,得到105条膛压曲线的最小轮廓和最大轮廓,如图7所示。
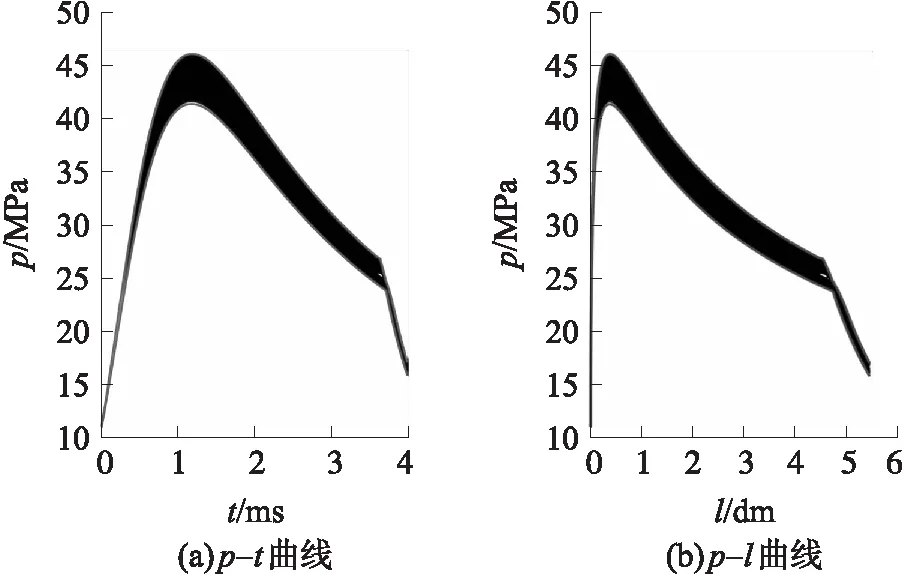
图7 随机发射药火药力对某无后坐炮内弹道膛压曲线分布区域的影响
图7中,最大膛压附近的膛压跳动最大值为4.490 6 MPa,炮口附近的膛压跳动最大值为1.210 1 MPa。
2.5 药室容积随机模拟
2.5.1 药室容积的制造误差
首先假设无后坐炮发射药药厚、弹质量、发射药药量和发射药火药力恒定不变,环境温度即药温为常温(15 ℃),药室容积随机变化,服从正态分布。无后坐炮药室直径和药室长度制造公差带宽度分别为0.36 mm和0.52 mm,2.2节已介绍全弹尺寸公差带与尺寸标准差的关系,同理可估算出某无后坐炮药室直径和药室长度的标准差分别约为0.06 mm和0.09 mm,因此可得到随机的药室容积。
利用2.1的方法可知,随机模拟药室容积所得到的膛压曲线包络线并不是一组随机药室容积值中最大与最小所对应的膛压曲线。利用文献[1]的方法产生105个随机药室直径值和随机药室长度值,然后由药室容积的计算公式计算得到105个药室容积随机值,然后循环模拟内弹道过程105次,通过比较某时间(某行程)对应的压力值,得到105条膛压曲线的包络线,如图8所示。

图8 随机药室容积对某无后坐炮内弹道膛压曲线分布区域的影响
图8中,最大膛压附近的膛压跳动最大值为0.537 4 MPa,炮口附近的膛压跳动最大值为0.413 7 MPa。制造公差控制良好,药室容积的随机变化对无后坐炮内弹道膛压曲线的分布区域影响很小,可忽略不计。
2.5.2 药室容积磨损
药室容积变化包括药室长度与药室内径的变化,连续发射多发炮弹时,火药气体对内膛不断地烧蚀冲刷,使火炮的药室容积不断增大。根据文献[8]给出的130 mm加农炮内径磨损量与射弹数的变化关系以及药室长度增长量与射弹数的变化关系,用回归的方法可得内径磨损量Δd与射弹发数N的关系式以及药室长度增长量ΔL与射弹发数N的关系式。
药室长度增长量ΔL与射弹发数N的关系式:
ΔL=5.478×10-8N3-7.692×10-6N2+0.015 75N-0.174 8
(4)
内径磨损量Δd与射弹发数N的关系式:
Δd=1.936×10-9N3-6.171×10-6N2+0.010 3N+0.119 9
(5)
把回归结果和实验数据绘成曲线,如图9(a)和图9(b)所示。从图中可以看出:离散点与回归曲线符合很好;此外由相关系数可知,图9(a)的相关系数ra=0.999 8,图9(b)的相关系数rb=0.999 1,即拟合曲线很接近真实情况。
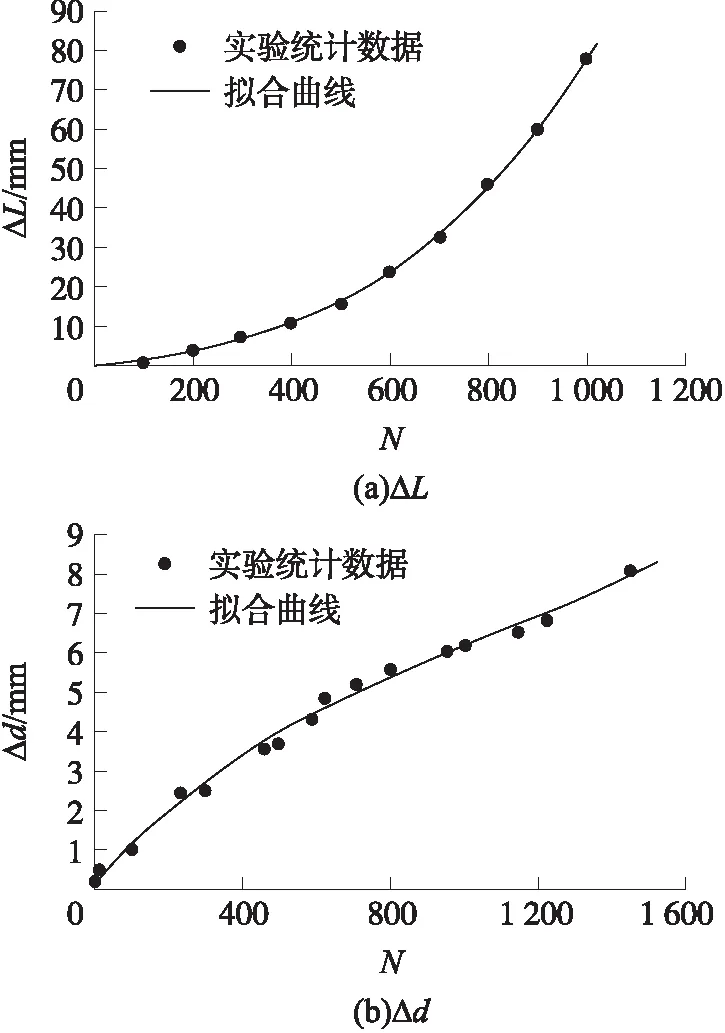
图9 药室长度增长量、内径磨损量与射弹数关系回归曲线
文献[16]提到瑞典M3无后坐炮的设计寿命为500发,但是美军靶场测试中曾经发射2 360发炮弹仍然完好。据此,将某无后坐炮的设计寿命取为1 000发。可根据式(7)和式(8)计算出130 mm加农炮在发射1 000发射弹后的内径磨损量Δd=5.43 mm和药室长度增长量ΔL=62.66 mm。在没有无后坐炮磨损量实验数据的背景下,现假设在相同射击炮弹数下,磨损量与最大膛压成正比。因此,可得某无后坐炮的最大设计内径磨损量Δdmax=0.62 mm和最大设计药室长度增长量ΔLmax=8.00 mm,进而由药室容积计算公式得到最大设计药室容积磨损量。由于在105次随机模拟下,无后坐炮药室容积已磨损到极限,因此,可取最大设计药室磨损量下的药室容积进行内弹道随机模拟。
2.6 分析与讨论
综上所述,发射药药厚的随机变化对膛压曲线分布区域的影响最大,且在整个内弹道过程中影响整个身管的膛压,其中最大膛压附近的膛压跳动最大值为5.247 3 MPa;发射药药量的随机变化对无后坐炮内弹道膛压曲线的分布区域影响较小,且发射药药量的随机变化影响整个内弹道过程的膛压,发射药药量标准差σmw=1 g时,其最大膛压附近的膛压跳动最大值为1.255 7 MPa;随机弹质量对无后坐炮内弹道膛压曲线的分布区域影响较小,且随机弹质量主要影响炮口附近压力值,其最大膛压附近的膛压跳动最大值为0.775 3 MPa;随机发射药火药力对无后坐炮内弹道膛压曲线的分布区域影响较小,发射药火药力的变化影响整个身管的膛压,且对最大膛压附近的影响相对较大,其最大膛压附近的膛压跳动最大值为4.490 6 MPa;随机药室容积(不考虑药室使用磨损)的随机变化对无后坐炮内弹道膛压曲线的分布区域影响很小,可忽略不计,但是必须考虑在多次随机模拟下药室容积的扩张,此时应取最大设计磨损量下的药室容积进行解算。
3 不同温度下4种装填参量随机模拟
由文献[17]知,火炮在作战条件下使用时,装药温度受环境温度影响很大。为了保证安全,在设计身管时,膛内压力必须考虑装药温度的变化。目前,常用的温度设定是:常温为15 ℃,高温为+50 ℃,低温为-40 ℃。
设装药温度为θ,装药温度改变量Δθ=(θ-15) ℃。当θ=50 ℃时,Δθ=35 ℃;当θ=-40 ℃时,Δθ=-55 ℃。装药初温变化,最大膛压也要变化,其变化值为
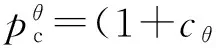
式中:cθ为最大压力修正系数。
初步计算时可以采用如下的关系式:硝化棉系火药,cθ=0.002 7cθk;硝化甘油系火药,cθ=0.003 5cθk。其中,cθk为压力全冲量修正系数,随装填密度Δ及最大压力pc的不同而变化,查阅文献[9]可得到系数cθk的值。
由此可计算出“温度影响系数”:J=1+cθΔθ。
只要在第2节所提的内弹道的燃速方程中乘以相对应的“温度影响系数”,就可得相对应温度下的膛压曲线。
综上所述,单个随机因素对内弹道膛压曲线包络线影响较大的有弹质量 、药量、火药力和药厚。
现取最大设计药室磨损量下的药室容积,并在高温(50 ℃)、常温(15 ℃)和低温(-40 ℃)下,随机模拟各影响因素,得到膛压曲线包络线。
根据文献[1]可知,影响膛内射击过程的因素是一个多维的问题。为了简单起见,假定药温为15 ℃,不考虑点火过程的随机因素,考虑弹质量、装药量(σmw=1 g)、发射药药厚和发射药火药力等4个装填参量的随机变化。
四维正态随机变量(Y1Y2Y3Y4)的协方差矩阵为

(6)
式中:Kij=E[(Yi-μi)(Yj-μj)]。
(7)
记
则
Σ=CCT
(8)
由式(8)得:
(9)
随机变量Y1,Y2,Y3,Y4分别代表弹质量、发射药火药力、发射药药量和发射药药厚的随机值。根据它们已知的分布可抽样一组随机值,带入内弹道方程组,得到一条膛压曲线,如此循环,可得大量内弹道膛压曲线,并得到其包络线。
高温、常温和低温下的解算结果如图10~图12所示。
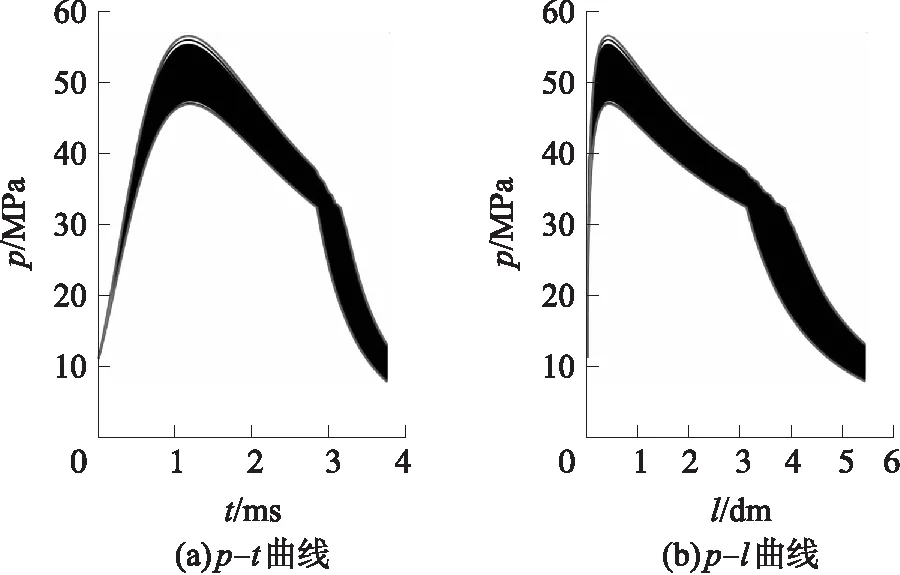
图10 高温(50 ℃)下4种随机因素对某无后坐炮内弹道膛压曲线分布区域的影响
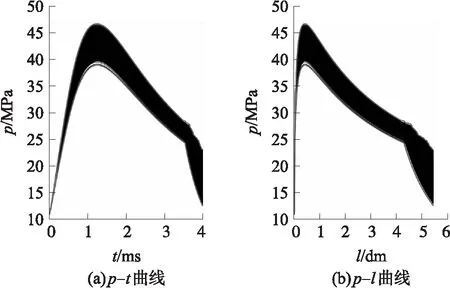
图11 常温(15℃)下4种随机因素对某无后坐炮内弹道膛压曲线分布区域的影响
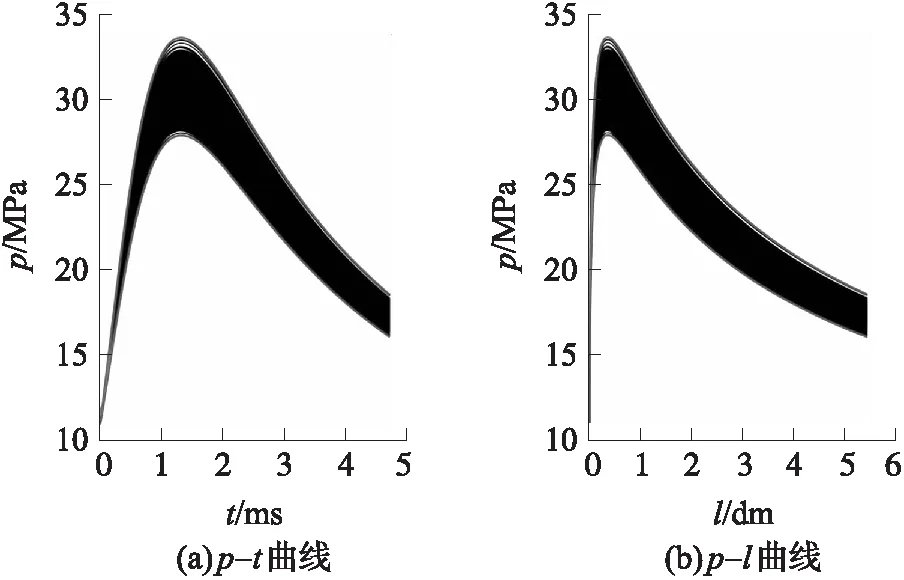
图12 低温(-40 ℃)下4种随机因素对某无后坐炮内弹道膛压曲线分布区域的影响
由图10~图12可知,最大膛压附近的膛压跳动最大值和炮口附近的膛压跳动最大值,在高温时分别为14.088 8 MPa,6.352 6 MPa;在常温时分别为7.749 8 MPa,10.832 2 MPa;在低温时分别为5.660 3 MPa,2.614 7 MPa。
4 结论
在高温(50 ℃)、常温(15 ℃)和低温(-40 ℃)下,考虑药厚、火药力、药量和弹质量4个随机因素同时对某无后坐炮内弹道膛压曲线轮廓的影响,随机模拟各影响因素,得到膛压曲线包络线。在不同温度下,4个随机因素对无后坐炮内弹道膛压曲线的分布区域影响都较大,且影响整个身管和内弹道的膛压分布,同时比单个随机因素对无后坐炮内弹道膛压曲线的分布区域影响更为明显,其中高温、低温和常温下最大膛压附近的膛压跳动最大值分别为14.088 8 MPa,5.660 3 MPa,7.749 8 MPa。因此,高温下膛压曲线的上包络线可用来对某无后坐炮身管和弹体进行强度校核,低温下膛压曲线的下包络线可用来分析某无后坐炮引信的解除保险性能。
本文在考虑药厚、火药力、药量和弹质量的随机性基础上,应用蒙特卡洛方法,结合无后坐炮内弹道经典模型,对不同随机因素对弹道性能造成的影响进行了随机模拟,计算结果能较好地反映出膛内射击过程的变化规律,并对某无后坐炮的系统设计有一定的指导意义。同时,在制造生产无后坐炮时,必须将发射药和弹丸的制造误差控制在令人满意的范围内,这样某后坐炮的膛压跳动会相对较小,有利于提高某无后坐炮的射击精度和使用寿命。
[1] 金志明. 内弹道循环的随机模拟[J]. 南京理工大学学报,1987(3):42-51.
JIN Zhiming. Stochastic simulation of inner trajectory cycle[J]. Journal of Nanjing University of Science and Technology,1987(3):42-51. (in Chinese)
[2] 鲍廷钰,张兆钧,邱文坚,等. 火药不均一性引起初速散布的密闭爆发器试验预估[J]. 南京理工大学学报,1994(5):25-32.
BAO Tingyu,ZHANG Zhaojun,QIU Wenjian,et al. Experimental prediction of closed bursts caused by the nonuniformity of gun powder[J]. Journal of Nanjing University of Science and Technology,1994(5):25-32. (in Chinese)
[3] 冯德成,翁春生,白桥栋,等. 随机因素对弹道性能影响的数值仿真[J]. 火炮发射与控制学报,2005(1):1-5.
FENG Decheng,WENG Chunsheng,BAI Qiaodong,et al. Numerical simulation of the effect of stochastic factors on trajectory performance[J]. Journal of Gun Launch & Control,2005(1):1-5. (in Chinese)
[4] NEVES A,MENDES E,SCHILLER L,et al. Recoilless gun:analysis of internal and external ballistics[C]//The 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Cincinnati:AIAA,2007:5160.
[5] 曹永杰,张向明,李志飞. 基于液态平衡体的无后坐炮内弹道研究[J]. 弹道学报,2016,28(3):71-75.
CAO Yongjie,ZHANG Xiangming,LI Zhifei. Research on interior ballistics of recoil gun based on liquid equilibrium[J]. Journal of Ballistics,2016,28(3):71-75. (in Chinese)
[6] 方再根. 计算机模拟和蒙特卡洛方法[M]. 北京:北京工业学院出版社,1988.
FANG Zaigen. Computer simulation and Monte Carlo method[M]. Beijing:Beijing University of Technology Press,1988. (in Chinese)
[7] 张晋华,闻泉,王雨时,等. 应用蒙特卡罗方法计算弹丸偏心距[J]. 探测与控制学报,2016,38(5):42-48.
ZHANG Jinhua,WEN Quan,WANG Yushi,et al. Application of Monte Carlo method to calculate projectile eccentricity[J]. Journal of Detection & Control,2016,38(5):42-48. (in Chinese)
[8] 张小兵. 枪炮内弹道学[M]. 北京:北京理工大学出版社,2014.
ZHANG Xiaobing. Interior ballistics of guns[M]. Beijing:Beijing Institute of Technology Press,2014. (in Chinese)
[9] 王连荣,张佩勤. 火炮内弹道计算手册[M]. 北京:国防工业出版社,1987.
WANG Lianrong,ZHANG Peiqin. Manual of artillery interior ballistics calculation[M]. Beijing:National Defense Industry Press,1987. (in Chinese)
[10] 王晓鹏,王雨时,卢凤生,等. 155 mm口径火炮榴弹结构特征数分布特性研究[J]. 探测与控制学报,2015,37(5):66-72.
WANG Xiaopeng,WANG Yushi,LU Fengsheng,et al. Study on the characteristic number distribution characteristics of 155mm caliber artillery shrapnel[J]. Journal of Detection & Control,2015,37(5):66-72. (in Chinese)
[11] 中国人民解放军总装备部. 榴弹定型试验规程:GJB 4225—2001[S]. 北京:总装备部军标出版发行部,2001.
General Armament Department of Chinese People’s Liberation Army. Grenade shaping test procedure:GJB 4225—2001[S]. Beijing:General Armament Depentment’s Military Standard Publication and Distribution Department,2001. (in Chinese)
[12] 华恭,欧林尔. 弹丸作用和设计理论[M]. 北京:国防工业出版社,1975.
HUA Gong,OU Liner. Projectile function and design theory[M]. Beijing:National Defense Industry Press,1975. (in Chinese)
[13] 韩子鹏. 弹箭外弹道学[M]. 北京:北京理工大学出版社,2014.
HAN Zipeng. Rocket and projectile exterior ballistics[M]. Beijing:Beijing Institute of Technology Press,2014. (in Chinese)
[14] 闻泉,王雨时. 子母弹径向质心位置的蒙特卡罗模拟[J]. 弹箭与制导学报,2006,26(增刊6):403-405.
WEN Quan,WANG Yushi. A Monte Carlo simulation of radial centroid position of submunition[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(S6):403-405. (in Chinese)
[15] 李福平,等. 《火炸药手册》(Ⅱ)[M]. 西安:第五机械工业部第204研究所,1981.
LI Fuping,et al. Fire and explosives manual(Ⅱ)[M]. Xi’an:No. 204 Institute of the Fifth Machinery Industry Institute Department,1981. (in Chinese)
[16] 汉威. 步兵班的狙击炮——“卡尔·古斯塔夫”无后坐力炮[J]. 兵器知识,2015(8):52-57.
HAN Wei. Infantry class sniper gun:“Carl Gustav” recoilless guns[J]. Weapon Knowledge,2015(8):52-57. (in Chinese)
[17] 张相炎,郑建国,杨军荣. 火炮设计理论[J]. 北京:北京理工大学出版社,2005.
ZHANG Xiangyan,ZHENG Jianguo,YANG Junrong. Artillery design theory[J]. Beijing:Beijing Institute of Technology Press,2005. (in Chinese)

