稀布同心圆环阵列的优化设计

戴定成, 姚敏立, 金　伟, 张峰干

(1. 火箭军工程大学信息工程系, 陕西 西安 710025; 2. 火箭军工程大学初级指挥学院, 陕西 西安 710025)

0　引　言

同心圆环阵列(concentric ring array, CRA)因其良好的几何对称特性以及全方位角扫描能力,受到越来越多研究者的关注[1-15]。为了在一定的约束条件下降低天线的峰值旁瓣电平(peak sidelobe level, PSLL)以及阵元数量,获得更好的天线性能,各国学者进行了大量的探索,提出了一系列的方法。从阵列结构看,这些方法可以分为两类,第一类是稀疏的方法[2-5],即以均匀排布(通常阵元间隔为0.5λ)的阵列为基础,根据优化结果选择一部分阵元不予激励;第二类是稀布的方法[6-14],在满足约束条件的前提下,阵元被随机地放置在天线平面上。稀布阵列的阵元位置相较于稀疏阵有更大的自由度,因此有着更加广阔的应用前景,但同时由于该问题的高度非线性,其优化难度也更大。

文献[1]将混合遗传算法(hybrid genetic algorithm, HGA)应用到同心圆环阵列综合中,以圆环半径以及各圆环上的阵元数量作为优化对象,对同心圆环阵列进行了综合,取得了较好的效果。文献[9]提出了一种修正的实数编码遗传算法(modified real genetic algorithm, MGA),将圆环的半径作为优化对象,约束同一圆环上的阵元间隔,最后对所有阵元进行联合优化,降低了优化的计算量和模型的复杂性。文献[10]提出了一种改进的整数编码遗传算法(improved integer genetic algorithm, IIGA),提升了遗传算法的计算效率并能避免算法过早收敛。此外,还有差分进化[13](differential evolution, DE)算法,以及粒子群优化[14](particle swarm optimization, PSO)算法等进化算法也被应用到天线阵列综合中。文献[6-7]利用凸优化对同心圆环阵列进行优化求解,能够大大节省运算时间,但这些方法需要设定参考方向图,而如何确定合适的参考方向图,本身就是一个较为复杂的问题。

现有文献中很少对圆环数量进行优化分析,大多是根据固定的圆环数量来优化同心圆环阵列,针对不同数量的圆环,由于优化变量的维数不同,往往需要多次重复试验才能确定最优解。针对这一问题,建立了圆环半径的映射函数,使圆环不同数量的种群个体,能同时参与优化迭代过程。然后,借鉴和声搜索的思想,在差分进化算法中引入随机噪声,进一步建立了保留概率和变异概率的动态模型,提出了一种改进的差分进化算法,实现了保留概率以及变异概率随迭代次数动态变化,进一步提高了算法的全局搜索能力。最后进行了蒙特卡罗仿真实验,检验了算法的性能。

1　稀布同心圆环阵列的数学模型

1.1　同心圆环阵列的方向图

假设一个同心圆环阵列有Nr个圆环,Ne个方向性一致的阵元,结构如图1所示,则对应的阵因子(array factor,AF)为

(1)

式中,波数k=2π/λ,λ是波长;Im(m=1,2,…,Ne)是阵元激励电流;rm是第m个阵元对应的半径;φm是方位角,(rmcosφm,rmsinφm)是第m个阵元对应的坐标；u=sinθcosφ,v=sinθsinφ,θ和φ分别是俯仰角和方位角。文中主要研究均匀激励的同心圆环阵列方向图综合问题,因此Im=1。在稀布同心圆环阵列中,为了获得笔形波束以及360°几何对称的良好性能,通常各圆环的半径是随机分布的,不同圆环上的阵元间隔不全相等,而同一圆环上的阵元是均匀分布的。 为了避免互耦带来的不良影响,一般要求圆环之间以及阵元之间的间隔不小于最小间隔dc,通常dc=0.5λ。 根据这一要求,可以求出每个圆环上可放置阵元数量的最大值。

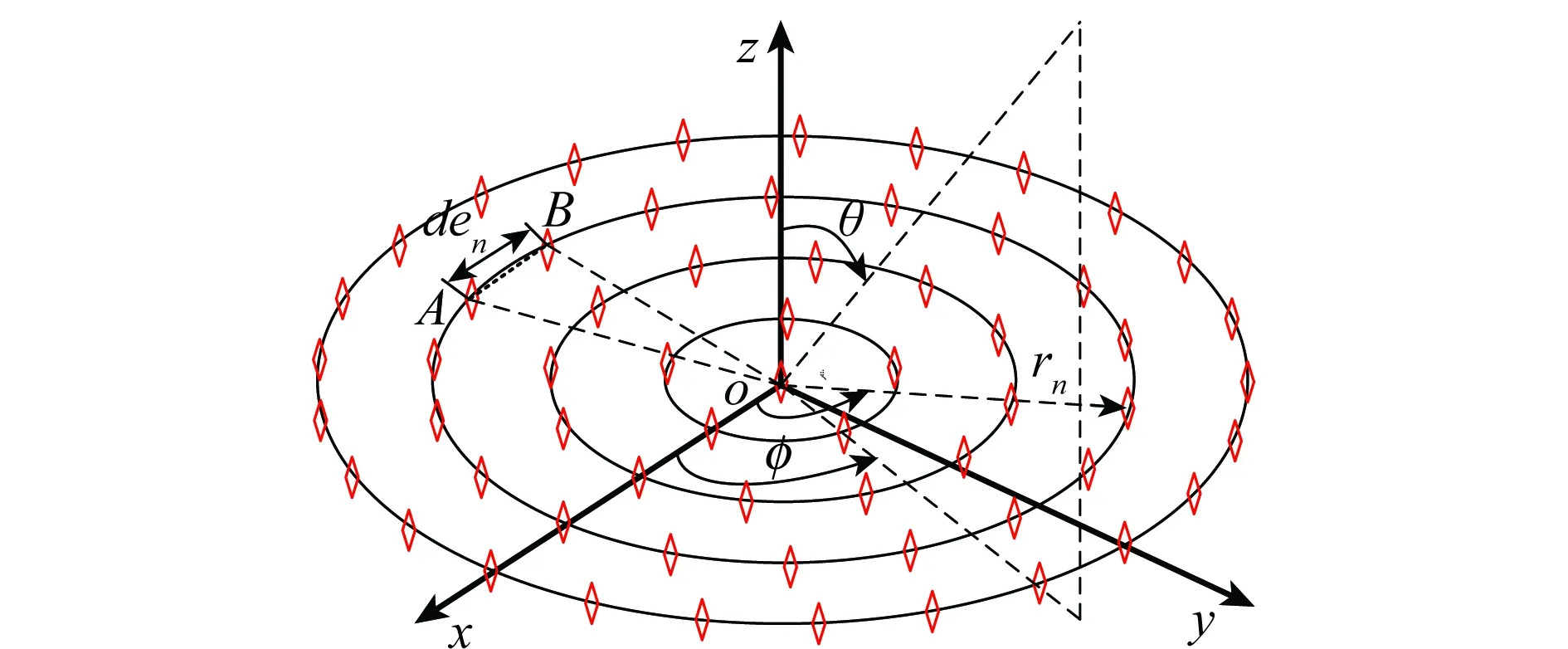
图1　同心圆环阵列结构图

如图1所示,假设第n个圆环的半径为rn,阵元间隔是den,则两个相邻阵元A和B之间的圆心角为

∠AOB=2arc sin(den/2rn)

(2)

那么该圆环最大可放置阵元数可表示为

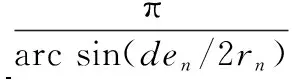
(3)

为了获得更好的天线性能,对于同心圆环阵列,其优化目标一般设为全平面的峰值旁瓣电平,即

(4)

式中,(u0,v0)是主瓣区域;(u,v)是主瓣以外的区域。

1.2　映射函数及优化模型

现有文献中,通常是根据固定的圆环数量来优化圆环半径以及各圆环上的阵元间隔,而对于不同圆环数量的优化,却鲜有报道。 为了获得更好的天线性能并减少优化实验次数,将圆环数量也纳入到优化对象当中。

首先,以圆环间隔作为变量,构造M维随机变量D=[d1,d2,…,dM],其中di∈[dc,λ]。 根据D计算初始圆环半径H=[h1,h2,…,hM],其中

(5)

找到满足hk0+1>L且hk0≤L的k0,k0便是由D决定的圆环数量。

其次,取前k0项di进行映射以满足天线孔径约束条件，即

(6)

Sp=L-k·dc

(7)

(8)

(9)

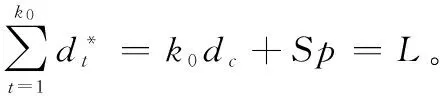
将D作为优化变量,可以保证不同圆环数量的种群个体,其优化变量的维数一致,对于某一确定的D,其对应的圆环半径R*也是唯一确定的。 这样不同圆环数量的个体便能够同时参与优化过程,执行交叉变异等步骤。 记该映射关系为R*=g(D)。

根据上述分析,可以将圆环阵列天线的优化模型写为

(10)

2　改进的差分进化算法

2.1　算法基本流程

标准的差分进化算法采用交叉替换等操作,利用候选解的差异干扰量来产生新个体,具有结构简单、全局搜索能力较强等特点。 然而如何选择合适的变异和交叉概率以提高算法的搜索速度以及全局收敛能力,是制约差分进化算法性能的重要因素。

乐师在创作过程中通常利用3种方法使各乐器产生美妙的和声共鸣,即:乐师的记忆、小幅修改现有乐器搭配以及偶然的创作灵感。 和声搜索算法[15]模拟这一创作过程,构造了3种种群进化策略,即:①继承上一代种群个体;②对上一代个体进行交叉变异等小幅度微调;③注入随机噪声。 和声搜索算法参数较少,结构简单,在解决多维复杂优化问题上展现出了良好的全局搜索性能。 文献[16-17]提出了一种基于和声搜索的差分进化算法,引入和声搜索的思想,在产生新的可行解过程中注入随机噪声,可以改善种群的结构,增加种群的多样性以及算法的全局收敛能力。 文献[18]针对和声搜索算法的两个关键参数(和声微调概率与和声微调幅度)进行了研究分析,提出了多种适应不同场景的和声微调概率模型。 在文献[16-18]的研究基础上,提出一种保留概率和差分变异概率时变的改进差分进化(improved differential evolution, IDE)算法。其算法流程如下:

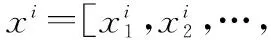
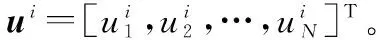
(11)

式中,i=1,2,…,NP;j=1,2,…,N;randj是[0,1]之间的随机数;random代表在优化变量取值范围内随机生成的分量,即随机噪声。构造保留和变异概率的时变模型为

(12)

式中,NI代表最大迭代次数;nt代表当前迭代次数;P(t)代表CR或者MR;Pmax代表CR或者MR对应的最大概率;Pmin代表最小概率。 根据式(12)可绘出概率变化曲线如图2所示。

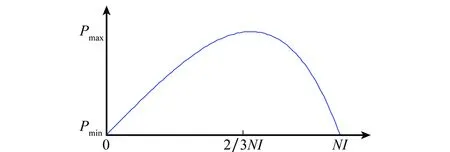
图2　保留和变异概率变化曲线

利用式(12)构造的保留和变异概率,在优化迭代的前半部分,保留和变异的概率逐渐变大,能更好地继承种群和变异个体的成分,有利于提高算法的局部搜索能力。 而后半部分,保留和变异概率逐渐变小,能更好地吸收随机噪声的成分,有利于增强种群多样性,跳出局部最优解。 2/3处也并非固定值,可以根据实际情况修正概率模型,进而调整最大概率出现的时间点。

步骤3更新种群。 如果新可行解ui的适应值优于父代xi,则用ui代替xi进入下一步迭代。

步骤4终止判断。 若迭代次数达到预定最大值,则终止算法,否则继续步骤2和步骤3,迭代次数加1。

2.2　标准函数测试实验

为了检验IDE算法的全局寻优能力和收敛精度,利用4组标准测试函数对IDE算法和DE算法进行对比实验。各测试函数的编号、名称、表达式、变量取值范围、目标值以及寻优类型如表1所示。

表1　进化算法测试函数

函数f1的全局极大值被极小值包围,传统算法极易陷入局部最优解,当(x,y)=(0, 0)时f1取得最大值3 600。 函数f2是基于De Jong函数的局部最小值规则分布的多模函数,该函数有多个局部极小值,搜索算法容易过早收敛,该函数在(x,y)=(0,0)时取得最小值0。函数f3与f2类似,同样包含大量局部最优解,只有在(x,y)=(0, 0)时取得全局最小值0。 函数f4在(x,y)=(0,0)时取得全局最大值0,而距离最优解kπ(k∈Z+)处,存在无数个局部极大值。 以上4组函数能够充分检验算法的全局搜索能力和收敛精度。

仿真的基本参数设置为:迭代次数NI=1000,种群规模NP=30,标准DE的保留概率CR=0.9,IDE算法的保留概率CR最大值和最小值分别为0.9和0.8,变异概率MR的最大值和最小值分别为0.8和0.4。对于每一项测试函数均进行100次蒙特卡罗仿真。为了保证实验的公平性,每次独立实验两种算法的随机初始种群均设为相同。

测试的硬件条件为一台DELL工作站,其CPU为Intel Xeon E31240 @ 3.3GHz,内存为16GB。 所有仿真程序均在Win 7操作系统下Matlab 2014a软件中运行。

对各测试函数100次独立实验结果的最优值、最差值、平均值、标准差以及寻优成功率(即在100次独立实验中搜索到全局最优解次数的比率)进行统计分析,如表2所示。

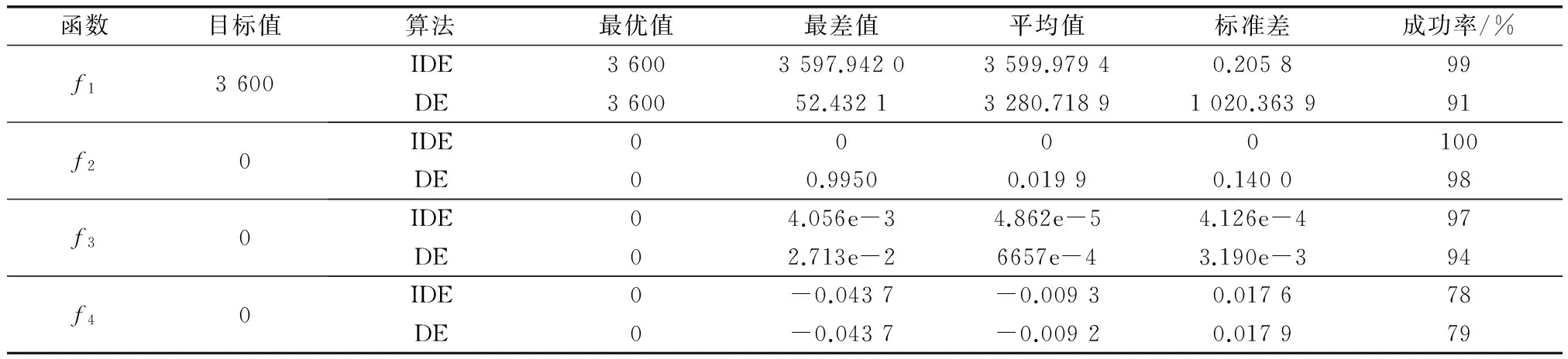
表2　IDE和DE测试结果对比

从表2中可以看出,在f1～f3函数测试中,IDE算法在搜索成功率以及均值方差等指标上均明显优于DE算法。特别地,在f1函数测试中,IDE算法的搜索成功率比DE高8%,IDE算法的最差值与目标值相差不到0.1,而DE算法的最差值与目标值却相差甚远,这说明DE算法容易陷入局部最优。尽管f4函数测试中IDE算法搜索成功次数比DE算法少一次,但IDE算法的最差值和最优值与DE算法相同,均值和标准差与DE算法相近。因此,通过该实验可以说明,IDE算法的全局搜索能力以及收敛精度是优于DE算法的。

3　实验仿真与分析

为了检验提出算法的性能,针对只优化圆环半径、只优化阵元间隔和同时优化圆环半径与阵元间隔等3种情况进行实验仿真。 选择DE/best/1作为差分进化算法的变异策略。 仿真实验的参数设为:CRmax=0.95,CRmin=0.75,MRmax=0.85,MRmin=0.2,F=0.5。 因文献[1]并未明确给出HGA算法的种群规模和迭代次数,根据文献[9]中MGA方法的种群规模100、迭代次数200,以及文献[10]中IIGA的种群规模30、迭代次数200,不失一般性,将IDE算法的参数设为:种群规模NP=30,最大迭代次数NI=100。 针对各实验场景分别进行100次蒙特卡罗仿真实验。

由于文献[9-10]中未对圆环半径和阵元间隔进行单独优化研究,因此场景1和场景2只与文献[1]中的HGA的实验结果进行对比。 场景3同时优化圆环半径和阵元间隔的实验与HGA,MGA以及IIGA一同进行比较。

3.1　场景1——仅优化圆环半径

假定圆环阵列天线的孔径为L=4.98λ,各圆环的阵元间隔均设为den=0.5λ,各圆环上的阵元均匀排布,以圆环半径作为优化对象进行优化。 IDE的蒙特卡罗仿真结果如图3所示。 IDE算法的蒙特卡罗仿真得到的PSLL平均值为-24.35 dB,方差为0.032 dB。蒙特卡罗仿真的最优PSLL为-24.67 dB,该结果比HGA方法低1.73 dB。

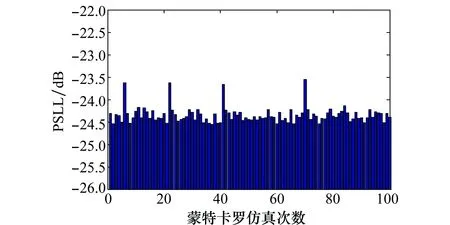
图3　场景1蒙特卡罗仿真结果

最优结果对应的方向图及截面图如图4所示,各圆环对应的半径及阵元数量如表3所示。各圆环上的阵元数量根据式(3)可计算得到。

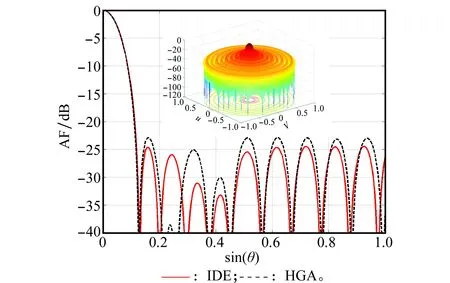
图4　场景1最优结果方向图

场景L/λ算法PSLL/dBNe圆环编号1编号2编号3编号4编号5编号6编号714.98IDE-24.67217rn0.61.121.622.263.073.824.98Nn7142028384762HGA-22.94201rn11.592.142.883.664.98-Nn121926364562-

注1):L为阵列孔径,Ne为阵元数量,rn为圆环半径,Nn为对应圆环上的阵元数量,下同。

3.2　场景2——仅优化阵元间隔

假设阵列的孔径为L=4.5λ,各圆环间隔固定为0.5λ,以各圆环上的阵元间隔作为优化对象,进行优化。蒙特卡罗仿真实验结果如图5所示。100次独立实验中,IDE算法得到的平均PSLL为-26.98 dB,方差为0.183。IDE算法最优PSLL为-27.41 dB,比HGA方法的最优解低1.83 dB。

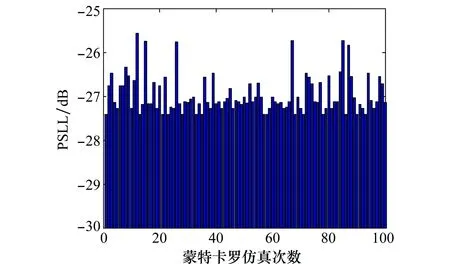
图5　场景2蒙特卡罗仿真结果

IDE算法的最优解对应的方向图与截面图如图6所示。从图6中可以看出,IDE算法在没有明显拓展主瓣宽度的情况下,有效降低了峰值旁瓣电平。 IDE算法获得的最优解的如表4所示,在仅优化阵元间隔的情况下,IDE求得的第8个圆环上阵元数量为0,即实际圆环数量只有7个。

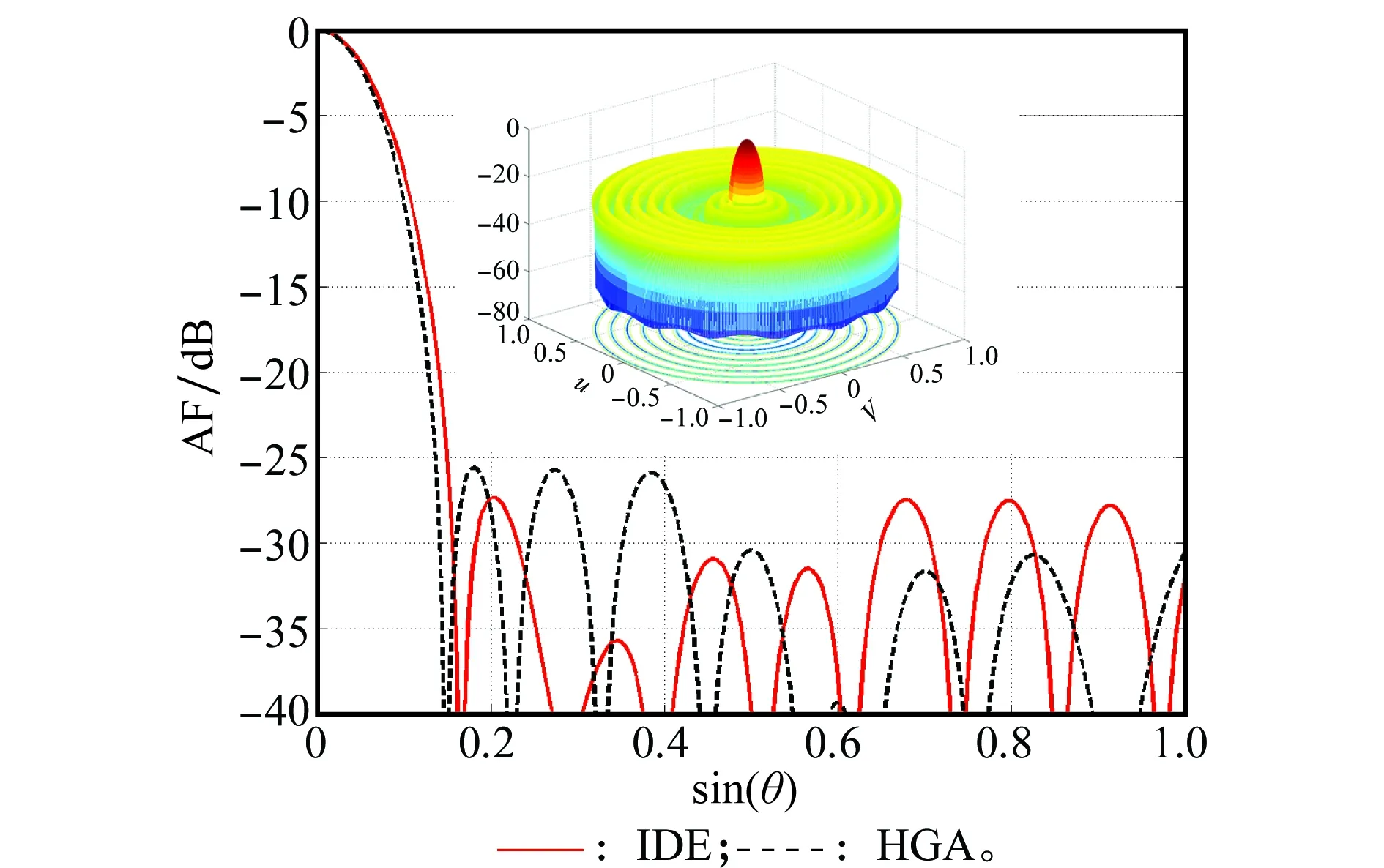
图6　场景2最优结果方向

场景L/λ算法PSLL/dBNern0.511.522.533.544.524.5IDE-27.41169Nn=6Nn=12Nn=18Nn=25Nn=25Nn=26Nn=25Nn=0Nn=31HGA-25.58183Nn=6Nn=12Nn=18Nn=25Nn=17Nn=23Nn=22Nn=27Nn=32

3.3　场景3——同时优化圆环半径与阵元间隔

假设同心圆环阵列孔径为L=4.7λ。利用IDE算法进行100次蒙特卡罗仿真实验的结果如图7所示。

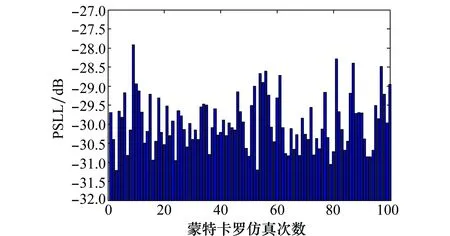
图7　场景3蒙特卡罗仿真结果

由于优化变量增加,因此同样的实验参数下,图7中最优解的方差明显要高于场景1和场景2。IDE在蒙特卡罗仿真实验中平均PSLL为-29.98 dB,方差为0.491,最优PSLL为-31.22 dB。最优方向图和截面图如图8所示,最优解与参考文献的对比如表5所示。在圆环数量相同的条件下,IDE算法比IIGA的PSLL提升了0.86 dB。

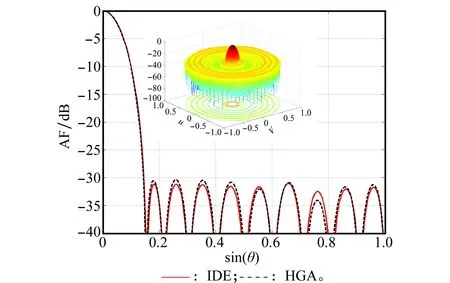
图8　场景3最优结果方向图

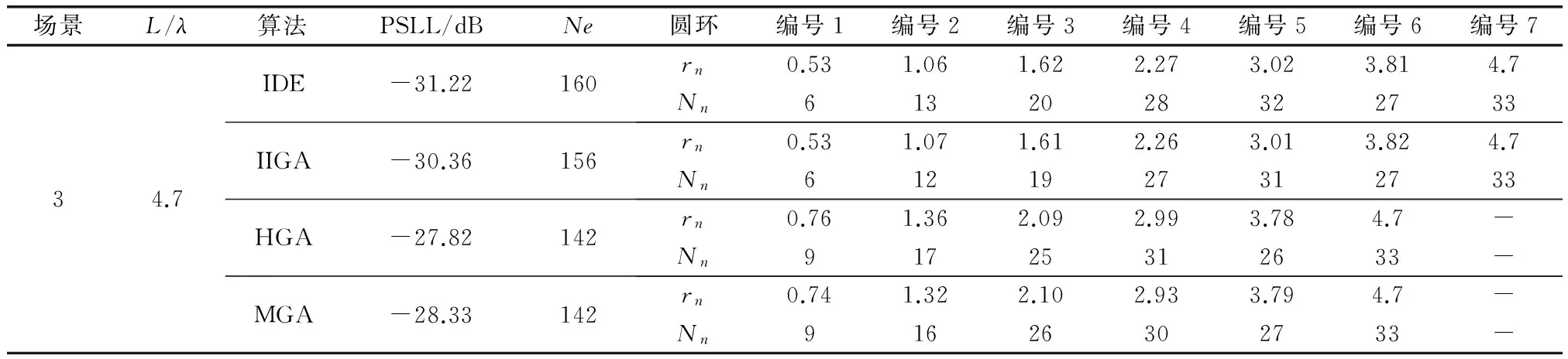
场景L/λ算法PSLL/dBNe圆环编号1编号2编号3编号4编号5编号6编号734.7IDE-31.22160rn0.531.061.622.273.023.814.7Nn6132028322733IIGA-30.36156rn0.531.071.612.263.013.824.7Nn6121927312733HGA-27.82142rn0.761.362.092.993.784.7-Nn91725312633-MGA-28.33142rn0.741.322.102.933.794.7-Nn91626302733-

3.4　实验结果分析

场景1中,根据第1.2节中提出的圆环半径映射方法,使用IDE算法得出的最优解有7个圆环,比HGA最优解多一个环,最终优化结果也优于HGA,这说明通过圆环半径的映射方法得到的最优解是有效的。蒙特卡罗仿真实验的方差很小,这说明IDE算法在针对圆环半径优化时,其稳定性和鲁棒性较强。

场景2中,针对固定圆环半径的阵列,只优化各圆环上的阵元间隔,与HGA相比,IDE算法最优解的阵元总数更少,但天线性能更优。这一方面证明了IDE算法具有较好的全局搜索能力,另一方面也说明PSLL与阵元数量没有必然的联系,通过合理的排布,可以用较少的阵元数量达到更优的天线性能。

场景3中,同时优化圆环半径与各圆环上的阵元间隔,IDE算法的圆环数量与IIGA的一致,比HGA和MGA方法多1个,最终结果也比HGA和MGA好。IDE算法的阵元总数只比IIGA多4个,而PSLL却低0.86 dB,这说明IDE算法能够在不显著增加阵元数量的情况下,有效降低阵列的峰值旁瓣电平。场景3中蒙特卡罗实验结果的方差比场景1和场景2更高,这一方面是因为同时优化阵元间隔和圆环半径增加了变量维数,导致了优化结果不确定性增大,另一方面是因为迭代次数较少,部分独立实验并未完全收敛所致。

根据上述3个不同场景的实验结果可以看出,IDE算法通过圆环半径映射方法以及时变的概率调整模型,提高了算法的全局搜索能力和计算稳定性,能有效降低同心圆环阵列天线的PSLL。

4　结　论

针对有阵元间隔约束和天线孔径约束的均匀激励同心圆环阵列综合问题,建立了圆环数量不等情况下的圆环半径映射函数,实现了对圆环数量的同时优化。在差分进化算法中,引入随机噪声,建立保留和变异概率的动态模型,提升了算法的全局搜索能力和计算稳定性。仿真实验结果表明,改进后的算法能有效降低同心圆环阵列的峰值旁瓣电平。

参考文献：

[1] HAUPT R L. Optimized element spacing for low sidelobe concentric ring arrays[J]. IEEE Trans.on Antennas and Propagation, 2008, 56(1): 266-268.

[2] PATHAK N N, MAHANTI G K, SINGH S K, et al. Synthesis of thinned planar circular array antennas using modified particle swarm optimization[J]. Progress in Electromagnetics Research Letters, 2009, 12: 87-97.

[3] GHOSH P, DAS S. Synthesis of thinned planar concentric circular antenna arrays——a differential evolutionary approach[J]. Progress in Electromagnetics Research B, 2011, 29(29): 63-82.

[4] SINGH U, KAMA T S. Synthesis of thinned planar concentric circular antenna arrays using biogeography-based optimisation[J]. IET Microwaves Antennas & Propagation, 2012, 6(7): 822-829.

[5] ZHANG L, JIAO Y C, WENG Z B, et al. Design of planar thinned arrays using a boolean differential evolution algorithm[J]. IET Microwaves Antennas & Propagation,2010,4(12):2172-2178.

[6] ZHAO X W, YANG Q, ZHANG Y. A hybrid method for the optimal synthesis of 3-D patterns of sparse concentric ring arrays[J].IEEE Trans.on Antennas and Propagation,2016,64(2):515-524.

[7] BUCCI O M, PINCHERA D. A generalized hybrid approach for the synthesis of uniform amplitude pencil beam ring-arrays[J]. IEEE Trans.on Antennas and Propagation,2012,60(1):174-183.

[8] ANGELETTI P, TOSO G, RUGGERINI G. Array antennas with jointly optimized elements positions and dimensions part Ⅱ: planar circular arrays[J]. IEEE Trans.on Antennas and Propagation, 2014, 62(4): 1627-1639.

[9] CHEN K S, ZHU Y Y, NI X L, et al. Low sidelobe sparse concentric ring arrays optimization using modified GA[J]. International Journal of Antennas & Propagation,2015,2015(147247): 1-5.

[10] 唐斌, 陈客松, 杨晓波. 圆形口径平面天线阵列的多约束稀布优化方法[J]. 电波科学学报, 2013, 28(1): 23-29.

TANG B, CHEN K S, YANG X B. An optimum method of sparse plane arrays with circular boundary[J]. Chinese Journal of Radio Science, 2013, 28(1): 23-29.

[11] 于波,陈客松,朱盼,等.稀布同心圆环阵列的降维优化方法[J].电子与信息学报,2014,36(2): 476-481.

YU B, CHEN K S, ZHU P, et al. An optimum method of sparse concentric rings array based on dimensionality reduction[J].Journal of Electronics & Information Technology,2014,36(2): 476-481.

[12] JIANG Y, ZHANG S, GUO Q, et al. Synthesis of uniformly excited concentric ring arrays using the improved integer GA[J]. IEEE Antennas & Wireless Propagation Letters, 2016,15:1124-1127.

[13] CHATTERJEE A, MAHANTI G K, MAHAPATRA P R S. Optimum ring spacing and interelement distance for sidelobe reduction of a uniform concentric ring array antenna using differential evolution algorithm[C]∥Proc.of the IEEE International Conference on Communication Systems, 2010: 254-258.

[14] ELSAIDY S, DESSOUKY M, KHAMIS S, et al. Concentric circular antenna array synthesis using comprehensive learning particle swarm optimizer[J]. Progress in Electromagnetics Research Letters, 2012, 29: 1-13

[15] KIM J, ZONG W, KIM E. Parameter estimation of the nonlinear muskingum model using harmony search[J]. Journal of the American Water Resources Association,2007,37(5):1131-1138.

[16] ZHANG F G, JIA W M, YAO M L. Linear aperiodic array synthesis using differential evolution algorithm[J]. IEEE Antennas & Wireless Propagation Letters,2013,12(9):797-800.

[17] 刘浩淼,贾维敏,张峰干,等.基于二进制差分进化算法的MIMO雷达阵列优化[J].微波学报, 2016, 32(4): 33-40.

LIU H, JIA W, ZHANG F, et al. Array optimization for MIMO radar based on binary differential evolution algorithm[J]. Journal of Microwaves, 2016, 32(4): 33-40.

[18] 韩红燕, 潘全科, 梁静. 改进的和声搜索算法在函数优化中的应用[J], 计算机工程, 2010, 36(13): 245-247.

HAN H Y, PAN Q K, LIANG J. Application of improved harmony search algorithm in function optimization[J]. Computer Engineering, 2010, 36(13): 245-247.