一类隐零点问题的解题策略

■东北师范大学附属中学　刘彦永

近年来,高考数学压轴题的热点聚焦在了函数的零点和极值点问题。笔者在教学实践中发现同学们对隐零点(零点不可求)问题没有系统的解决办法,常常望而生畏,不知所措。本文通过下面的典型题目探讨这类问题的三种基本解法,以明确这类问题的解题策略,提高解题效率。

题目1：设函数f(x)=ex-ax-2。

(Ⅰ)求f(x)的单调区间;

(Ⅱ)若a=1,k为整数,且当x＞0时,(x-k)f'(x)+x+1＞0,求k的最大值。

本题是2012年全国新课标卷Ⅱ文科第21题,题目限制条件比较新颖,采用设而不求的解法非常有效,这类题型的练习对同学们的思维有一定的启发性。

解析：(Ⅰ)函数f(x)的定义域为R,且f'(x)=ex-a。

当a≤0时,f'(x)＞0,f(x)在R上是增函数,f(x)的单调递增区间是R;

当a＞0时,令f'(x)=ex-a=0,得x=lna。

令f'(x)=ex-a＞0,得x＞lna,所以f(x)在(lna,+∞)上是增函数;

令f'(x)=ex-a＜0,得x＜lna,所以f(x)在(-∞,lna)上是减函数。

故f(x)的单调递增区间是(lna,+∞),单调递减区间是(-∞,lna)。

(Ⅱ)解法1：(分离参数、设而不求,转化为函数最值问题)

若a=1,则f(x)=ex-x-2,f'(x)=ex-1。

所以(x-k)f'(x)+x+1=(x-k)(ex-1)+x+1=x(ex-1)+x+1-k(ex-1)。

当x＞0时,(x-k)f'(x)+x+1＞0等价于x(ex-1)+x+1-k(ex-1)＞0。

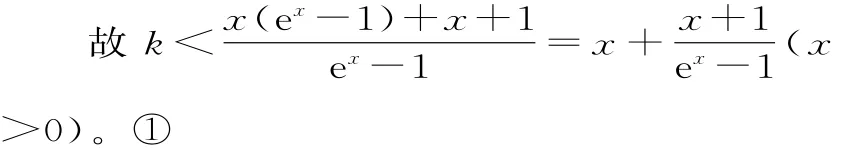
由于①式等价于k＜g(α)=α+1∈(2,3),故整数k的最大值为2。

解法2:(分类讨论,转化为函数最值问题)

当x＞0时,(x-k)f'(x)+x+1＞0等价于:(x-k)(ex-1)+x+1＞0。②

令g(x)=(x-k)(ex-1)+x+1(x＞0),g'(x)=(x-k+1)ex。

(1)当k≤1时,g'(x)＞0恒成立,g(x)在(0,+∞)上单调递增,g(x)＞1＞0,符合题意。

(2)当k＞1时,若x∈(0,k-1),则g'(x)＜0;若x∈(k-1,+∞),则g'(x)＞0。

故g(x)在(0,k-1)上单调递减,在(k-1,+∞)上单调递增。

由于②式等价于g(x)min=g(k-1)=k+1-ek-1＞0。

令h(k)=k+1-ek-1(k＞1),h'(k)=1-ek-1＜0,h(k)在(1,+∞)上单调递减。

且h(2)=3-e＞0,h(3)=4-e2＜0,故整数k的最大值为2。

由(Ⅰ)知,函数h(x)=ex-x-2在(0,+∞)单调递增。

而h(1)=e-3＜0,h(2)=e2-4＞0,所以h(x)在(0,+∞)上存在唯一的零点。

故g'(x)在(0,+∞)存在唯一的零点,设此零点为α,则α∈(1,2)。

当x∈(0,α)时,g'(x)＜0;当x∈(α,+∞)时,g'(x)＞0。

所以g(x)在(0,+∞)的最小值为g(α)。

又由g'(α)=0,可得eα=α+2,所以

解法3:(巧妙换元、数形结合,转化为切线问题)

当x＞0时,(x-k)f'(x)+x+1＞0等价于x(ex-1)+x+1-k(ex-1)＞0。

令t=ex∈(1,+∞),则问题等价于tlnt+1-k(t-1)＞0,即tlnt+1＞k(t-1)。

令g(t)=tlnt+1(t＞1),g'(t)=lnt+

问题等价于函数g(t)=tlnt+1的图像恒在过定点(1,0)的直线y=k(t-1)的上方。

作出草图即知临界值为过(1,0)作g(t)=tlnt+1的切线。

设切点坐标为(α,αlnα+1),则k切线=即lnα-α+2=0。

k切线=lnα+1=α-1∈(2,3),故整数k的最大值为2。

题目2：已知函数f(x)=axex-1,g(x)=lnx+kx。

(Ⅰ)求函数g(x)的单调区间;

(Ⅱ)当k=1时,f(x)≥g(x)恒成立,求a的取值范围。

当k≥0时,g'(x)＞0,g(x)在(0,+∞)上是增函数;

(Ⅱ)解法1：(分离参数、设而不求,转化为函数最值问题)

当k=1时,f(x)≥g(x)恒成立,即axex-1≥lnx+x恒成立。

故lnt+t=0,即t=e-t。

当x∈(0,t)时,p(x)＞0,h'(x)＞0;当x∈(t,+∞)时,p(x)＜0,h'(x)＜0。

h(x)max=h(t)=1。

解法2：(分类讨论,转化为函数最值问题)

当k=1时,f(x)≥g(x)恒成立,即axex-lnx-x-1≥0恒成立。

(1)当a≤0时,h'(x)＜0恒成立,h(x)在(0,+∞)上单调递减,h(1)=ae-2＜0,不符合题意。

(2)当a＞0时,令p(x)=axex-1(x＞0),p(x)在(0,+∞)上单调递增。

x∈(0,t)时,h'(x)＜0;x∈(t,+∞)时,h'(x)＞0。

h(x)min=h(t)=atet-lnt-t-1=-lnt-t=lna≥0,故a≥1。

解法3:(数形结合,转化为公切线问题)

当k=1时,f(x)≥g(x)恒成立,即axex-1≥lnx+x恒成立。

分别研究f(x)=axex-1和g(x)=lnx+x在(0,+∞)上的图像。

当a≤0时,axex-1≥lnx+x显然不恒成立。

当a＞0时,因为f'(x)=a(x+1)ex＞0,f″(x)=a(x+2)ex＞0,且g'(x)=+ 1＞0,g″(x)=-＜0,所以两个函数的草图(图1)和临界时的图像(图2)如下:

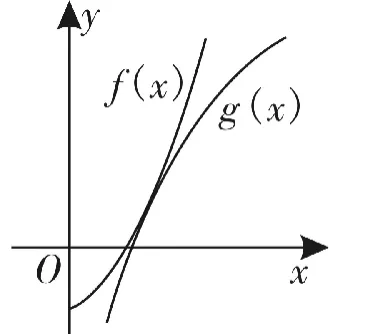
图2

图1

因此,只需找到临界状态对应的a即可。设临界时两曲线的公共点的横坐标为t,则有消去a得(t+1)(lnt+t)=0,即lnt+t=0。故atet-1=lnt+t=0,即atet=1,取对数有lna+lnt+t=0,得a=1。根据图像变化情况知a≥1符合题意。

隐零点问题是高考的一类重点和难点问题,解决此类问题主要有分离参数、分类讨论和数形结合三种方法,三种方法各有千秋,应具体问题具体分析。一般首选分离参数的方法,因为这样能将问题转化为不含有参数的函数的最值问题,直接降低了解答的难度。对于不易或不能分离参数的问题可采用分类讨论的方法。对于选择题或者填空题,我们可以利用技巧等价转化并应用数形结合快速得到答案。