数学教学：为理解而教，为理解而学
——“懂而不会”“会而不对”的成因分析及应对策略

☉四川省攀枝花市第十二中学校 张勇辉

一、问题提出

“懂、会、对”反映学生理解问题、解决问题的不同层次，由低到高呈递进关系.“懂”是“会”的基础，“真对”是“真懂”和“真会”的必然.在数学教学中，教师们总为一个普遍现象而苦恼，那就是学生“懂而不会”“会而不对”.这种现象到底是如何形成的？如何能有效地消减这种现象？许许多多的数学教师进行了大量的探究.笔者截取了日常教学的一些教学片段，选择了高中数学学习中一些常见的例习题，来分析学生学习中“懂而不会”“会而不对”的成因，探寻教学应对策略.

二、“懂而不会”“会而不对”的成因分析

例1 已知向量a，b，c为非零向量，求证：a·b=a·c⇔a⊥（b-c）.（高中数学人教A版必修4第二章《平面向量》P108习题2.4B组第一题）

学生在做这个题的时候基本上没有出错，解题思路如下：a⊥（b-c）⇔a·（b-c）=0⇔a·b-a·c=0⇔a·b=a·c.解题思路清晰流畅，向量垂直的条件、向量的数量积的运算用得到位，可以说是行云流水，这让我很放心，学生懂了！可是，一周后的一次检测，有这样一个填空题（选择正确的选择支），全班竟有的学生选择了这个选择支：已知向量a，b，c为非零向量，若a·b=a·c，则b=c.

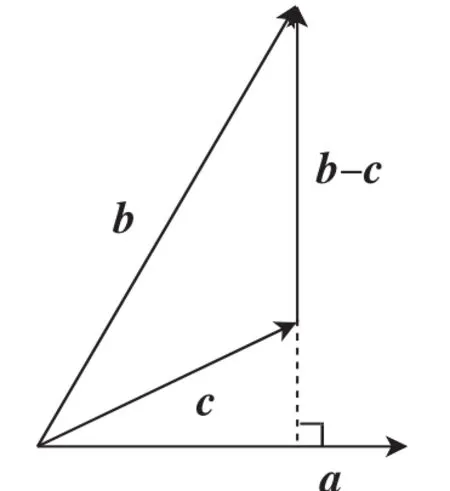
图1

问题出在哪儿？怪学生没有记住练过的那个习题的结论？显然不能.我问了几个出错的同学，他们给出了一些理由：①没细思考，当做实数运算处理了；②没弄明白，觉得有点儿像是对的便选了！其实，他们并没有真正弄懂a·b=a·c的含义：从数的方面看，a·b=a·c⇔|a||b|cosθ1=|a||c|cosθ2⇔|b|cosθ1=|c|cosθ2，从形的方面，则意味着向量b和c在向量a上的投影相等（如图1，显然a⊥（b-c））.

结语：从“懂”到“真懂”，需要思维的飞跃.学生所谓的“懂”，很多时候只是一种感觉，缺乏具体的衡量标准，懂得多与少、思维层次的深浅等等都是相对的.从本例来看，学生刚学完向量垂直的条件和向量的运算，在条件和结论间相互转换并没有太大的难度，但是，学生对a⊥（b-c）和a·b=a·c的意义及相关性（等价性）并没有进行深入的探究，进而出现后面的解题错误.实际上，如果没有教师的进一步引导，学生对这个问题的思考恐怕也很难深入.因此，教师在教学过程中的“导”非常重要，把学生从“懂”提升到“真懂”，就是一个把浅层思维导向深层思维的过程，进而达到真正理解的目标.否则，结果只可能是只“懂”不“会”！

例2 在△ABC中，b=

本题是学完正、余弦定理后的一个习题，学生1展示了她的解题思路：

①欲求a，应先求cos A（用余弦定理可求a），或求得sin A（用正弦定理可求a）；

②欲求cos A，sin A，先求sin C，cos C（利用cos A=-cos（B+C）=-cos B cos C+sin B sin C或sin A=sin（B+C））；

③sin C、cos C用正弦定理显然可求，所以a可求.

实际上，在解题的思路上，她是正确的，对于余弦定理、正弦定理的运用有了一定程度的理解，可以说她是“会”了.细心地检查，我们会发现，她在求sin C时出了错，正确的是：si，计算能力的不足，导致最后解题失败.假如，她没在求sin C时出错，后面的运算也完全正确的话，她是可以得出正确答案a=4或a=5.

但此处，我引着学生去反思，她选择的方法是最好的吗？结合已知条件，求a真的必须先求A吗？有学生反应过来：选择公式b2=c2+a2-2ca cos B，可以通过解关于a的一元二次方程，快速得到a=4或a=5.

反思两种解法，反映出了对余弦定理在理解上的差异，第一种解法的思路被完全固定在了“求第三边，必须知道另两边和所求边的对角”，第二种解法则跳出了这个框框，转换了思维角度，运用方程的思想灵活把握了余弦定理的本质“三边与其中一边所对角的关系”！思维品质上了一个台阶，选择了更适合的方法，运算量因此锐减！

结语：从“会”到“真会”，还要学会对方法进行合理的选择.选择的解题方法不同，往往意味着解题过程的繁简度不同，也直接反映出解题者效率的高低，但本质上却反应出学生对一个问题的理解程度！我们可以清晰地看到：从“会”到“真会”尚有一段艰难的路要跋涉.

我不经意地问：“这下对了吗？”“对了！”声音非常整齐.我装着准备写下一个题，突然不放心似地转身问：“真的对了吗？”“当然！”声音依然响亮！但我发现已经有同学不吱声了，我决定不点破，知道有人会用行动回答我啦.

第二天课前，我提前来到班上，发现教室后黑板上已经有学生给出了正确的解答：

因为si舍去，此时A+B＞π），从而以下略去）

就是这样一个常见的问题，经过了几次反复，才最终“拨云见日”，难怪学生感叹：要真正做对一个题太不容易！

结语：从“对”到“真对”，需要表达能力的提升，也需要对解题过程和结果进行重新审视.从“对”到“真对”，不仅要求学生要真懂，要学会选择解题方法，还要求学生用批判的眼光审视解题的过程，去伪存真.“真对”，是有硬性的标准检验的，换句话说，“真对”，太不易.

教学是教与学的双向过程，学生“懂而不会”“会而不对”，既有学生自身的原因，也有教师教学方面的原因，两者如影随形.

（一）学生方面的原因分析

第一，知识“断面”.数学学习和任何其他学习一样，都是一种认识的过程，而认识的过程都是通过自己已知的认知结构来加工新接触的信息，也就是说从已有的知识结构中提取有效的旧知识以吸取新知识.这就需要找到新旧知识的连接点，即它们共通的地方，需要学生在头脑中对新旧知识进行不断分化和重新组合.但是由于每个学生的个人认知情况不同，有的学生在某一个问题的学习中如果不能顺利实现新旧知识对接，就产生思维阻断.一旦形成障碍，学生的思维“链条”断裂，对新知识的学习只会停留于“表象”，所谓的“懂”也只是一种表象.

第二，思维“浅层”.根据英国的S.Pirie和加拿大的T.Kieren提出的数学理解动态模型分析，许多学生的数学学习只停留于模型的第一阶段，即“初步了解”.比如，在例1的学习中，学生基本了解了两向量垂直与向量数量积为0的关系，但浅尝辄止，没能从“形”的方向深入；基本了解了a·（b-c）=0⇔a·b-a·c=0⇔a·b=a·c的推断，但没有弄清这种转换的意义，因而当同一个问题a·b=a·c在别的背景中出现时，形不成有效联系.

第三，表达“障碍”.“说数学”是一种重要的数学能力，用口说，用笔“说”，都能很好培养学生的数学语言组织、逻辑思维和创新思维能力.然而在教学中，我们经常会发现不少学生不能阐述自己所学的知识，往往词不达意、逻辑混乱，不能用规范的语言（文字、符号等）书写.究其根源，还是因为学生对所学知识的来龙去脉没有厘清，对所要解决的问题厘不清思路，找不到解决问题的途径.

第四，方法“单一”.高中新课程新增了“三视图”，是教学生多角度审视数学问题的好素材.由于学生对概念、定理、公式的运用条件和知识背景不熟悉，解题时很容易抓住一个貌似可以突破的地方入手，很难做到多角度观察和思考，找到适合自己的最佳解题路径，结果不是处处碰壁就是走了弯路.加之缺乏总结和反思，在同一问题上反复碰壁也将成为必然，“盲人摸象”的寓言在他们身上重复上演.

第五，审视“缺失”.很多学生没有真正养成审视解题过程和结果的习惯，无法从定性分析和定量运算中发现解题中的错误.比如，有的学生解题中出现sin15°+，却发现不了错误；再比如，例3中，C为△ABC的内角，学生3算出，却没有发现其中的错误.由于缺乏审视，学习过程中的错误被掩藏了.

我们不难发现，学生“懂而不会”“会而不对”的真正根源都在于对知识没有真正的理解！

（二）教师教学方面的原因分析

从教师层面看，教学缺乏针对性是造成学生“懂而不会”“会而不对”的真正原因.由于实行师班教学制，数学教师的教学任务太重，一位教师上两个班甚至三个班，面对一百多位学生，很容易出现以下两个突出问题：一是对学生的学情分析不到位，不清楚学生学习的断层所在.教学上赶进度、撒大网，备课针对性不强，不能对所出现的问题进行准确分析，更谈不上准备充分的、针对性的材料弥补学生知识断层.二是由于数学知识的理解需要在反复的思考和多次琢磨中才能完成，而一个班级学生的基础、学习能力差异很大，有的学生理解一个问题可在很短的时间内完成，而有的学生则需要很长时间，教师很难准确判定学生对相关知识的理解程度.

即便是实施一些优秀的教学模式和方法，上述两个方面的问题也不同程度地存在，需要下大力气研究才能解决.比如，“先学后教”教学模式是对传统的“先教后学、课后作业”教学模式的颠覆性改革，倡导学生自主学习、合作探究、交流展示，学生是学习的主体，教师在整个教学的过程中扮演组织者、指导者的角色，相对于传统教学有其显著的优点.在实施的过程中，我们会发现有一些问题仍然不易解决，如学生自主学习的成果展示的“话语权”容易掌握在“先行先知者”手中，当堂检测的效果难以准确统计和评判，教师“零散”的点拨难以梳理知识的来龙去脉、构建完整的知识体系，提升思维水平等等.再比如，“变式训练”作为优秀的数学教学传统被长期坚持，但如果做不到促成学生思维“渐进式”生长，浅层次的“变式训练”，只能是让学生“依葫芦画瓢”，无法触及问题的本质，引发深入思考，其结果是既浪费了时间，又无法真正将学生的思维引向深入，理解性学习成为空谈.

三、关注理解性教学和学习是消减“懂而不会”“会而不对”的可行途径

美国国家研究理事会在《人是如何学习的》报告中，总结了国际近30年从脑科学、神经科学、行为科学、心理学和教育学等多个学科角度对人类学习的研究成果，提出了学习科学的概念，其中有三条突出的基本学习原则：（1）原有的理解；（2）事实性知识和概念框架对理解的作用；（3）自我监控的重要性.在此研究基础上，更进一步地提出了七个理解性学习的原则：（1）围绕学科的主要概念和原理形成结构；（2）运用已有的知识建构新理解；（3）运用元认知促进学习；（4）学习者之间存在差异；（5）学习者的动机；（6）在实践活动的情境中学习；（7）社会交互学习的共同体.这些原则同样适合数学学习.新课程改革，倡导建构性的学习过程观，把学习过程的重点从对事实的记忆转向了对过程的理解.理解性学习关注学生的学习基础，也关注过程的学习，重在获得对学科核心概念和原理的深层理解，是一种有效的、有意义的学习.

“懂而不会”“会而不对”的真正症结正是在于学生对知识和方法的理解程度不够.因此，要消减这种现象，必须关注理解性学习，并把它切切实实落实在教学的每一个环节中.

首先，稳扎稳打练基础.基本知识是解题的基础，我们每一位教师都能认识到基础知识的重要性，在教学过程中也都注重打基础，但是，很多时候、很多地方我们做得不够.一些值得推荐的做法有：（1）在学习新知识之前检测学生学前知识的掌握程度，它是进一步理解的基础，关系到学生对知识的建构；（2）坚持“日清”“周清”“月清”；（3）循环检测学生基础知识的掌握程度；（4）制订过关的标准，精心编制基础知识过关测试题，对学生进行逐级过关，界定学生基础知识掌握的层次，为进一步夯实基础提供有信度的依据.这项工作非常重要，不仅要求教师要掌握一定的测量理论，还必须具备非常扎实的专业功底，需要教师集体协作才有可能完成.

其次，活学活用练方法.基本知识和方法是分割不开的，前者是解题基础，后者是解题的策略、手段和途径，解题反过来又促进知识的内化、方法的活化.在学生掌握基础知识的同时，强化对学生进行解题方法训练.“一题多解”并不是说方法越多越好，最重要的是在学生理解掌握通性通法的基础上，选择最适合自己的、最佳的解法并固化下来，反复训练，才能有效地迁移.以一场经典羽毛球赛为例，我们常常惊叹球员精湛的球技，精准的击发、到位的防守令人叹为观止.这一切精彩的表现无不来自于球员艰苦的训练.发球、勾球、吊球、杀球，无不经过千万次反复训练，才能做到球到眼到、眼到心到、技由心生.数学学习也是如此.

第三，从从容容提能力.提能力是学生的期待，也是教师的责任，教师在提升能力方面起着非常重要的作用.需要强调的是，不能将打基础、练方法同能力培养割裂开来，夯实基础、熟练方法本身就能使学生获得能力，也是学生进一步提高能力的基础.学生能力的形成是“渐进式”的、“动态化”的，因此教师要把握好教学的进度和节奏，不能因为急于完成教学任务而加快学习进度，加大教学容量，超出学生理解的程度，而是要适时地为学生提供思考的机会，让学生拥有思考空间去思考有能力思考的问题，不断获得更好的理解.同时学生理解力的提高还需要交流和表达，要让学生积极参与交流，表达自己的观点和认识，促进学生对理解的反思，在反思的过程中对自我认知进行辨别和调整，促进能力的自然形成和提高.所谓“从从容容”，就是要顺其自然，拒绝拔苗助长！

理解是一种复杂的心理现象，理解性教学和理解性学习是一个复杂的过程.通过学生问题解决的表现去分析学生的理解程度，找出学生在理解上存在的困难，分析困难产生的原因，制定相应的辅助措施，才能真正促进学生对知识的理解，有效消减“懂而不会”“会而不对”现象.总之，懂、会、对——在理解中提升！

1.涂荣豹.数学建构主义学习的实质及其主要特征［J］.数学教育学报，1999（4）.

2.朱曼丽.基于理解的数学教学［J］.中学数学月刊，2012（2）.

3.罗新兵，石雪梅.数学理解性学习的条件分析［J］.中学数学教学参考，2012（12）.

4.胡青友.关注理解性学习［J］.教育科学论坛，2008（2）.H