浅谈整体思想在中学数学解题中的应用

山西省晋中市昔阳县中学校 李旭虹

一、整体思想的要点概述

（一）整体思想的定义

数学中的“整体思想”是学生必须掌握的数学思想方法之一。整体思想方法就是指在研究问题时从整体出发,对问题的整体形式、结构、特征进行综合分析、整体处理的思想方法。利用整体思想分析问题,往往可以找到最合理、最简捷、最实用的解题方法,起到化难为易、化繁为简的作用,提高解题效率。

（二）整体思想解题方法指导

第一，运用整体思想解题时，首先要拥有极强的整体意识，站在宏观的角度考虑问题。

第二，运用整体思想解题时，要有灵活的思维方式，从问题的正向、逆向等不同角度去看问题，运用集中、发散、直观、抽象等思维模式来考虑问题。

第三， 运用整体思想解题时，就是运用整体的集合性、非加和性、相对性、多维性及统一性，从不同的角度整体处理、整体代入、整体消元、整体变形等特性处理问题。

第四，运用整体思想进行问题转换时，一定要注意问题的等价性。

二、整体思想在中学数学解题中的应用

（一）整体思想在代数中的应用

1.在数学式中的应用

在解有关数学式问题时，有时需要进行整体的变形和构造，然后利用变形后的式子进行解题运算，从而达到解决问题的目的。

【例1】 已知m、n为两个不相等的实数，并且满足-的值。

分析：按照常规解法，根据已知条件分别求出m、n的值，再代入求解，这样计算会显得比较复杂.而通过观察所给条件，可以把m、n可以看成是方程的两个根，变形后根据根与系数的关系整体求解。

解：由且mn≠，得m、n是方程的两个不等实根.根据根与系数的关系可得：

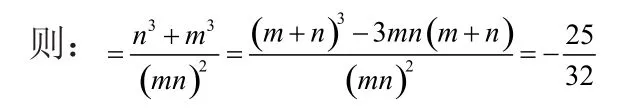
2.在不等式中的应用

从问题的整体结构入手，将问题看做一个整体M，接着构造一个相应的整体N，然后分析M，N之间的关系，从而达到解题的目的。

（二）整体思想在函数中的应用

1.在三角函数中的应用

在三角函数解题时，对角的整体认识和等价化归在其中有着很重要的作用。

【例2】 已知,α β是锐角，且满足

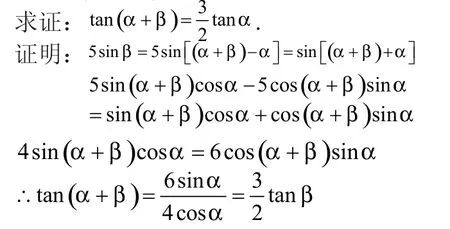
2.在复合函数中的应用

在一些复合函数的计算中，计算定义域是个难点，在计算的时候千万不要想当然，往往是“整体”替代范围不变，而不是单个范围不变.因此，掌握整体思想是必然的。

【例3】已知函数试求函数的表达式.

解：将2 3x+ 看成整体，看成整体，故有

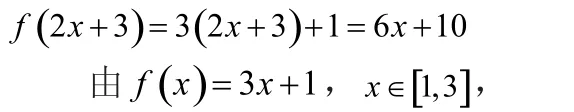
∴有计算可得

∴函数的表达式为：

3.在方程函数不等式整体运用

【例4】已知是定义在上的奇函数，且在上是增函数，若解关于x的不等式：

分析：整体思维意识指导我们，对不等式左端中括号内的应视为一个整体，把它看成是函数f(x)的自变量x所取的一个值，这样就可把不等式左端是为f(x)的一个函数值.同时也可将不等式右端的0看成是一个函数值，如于是站在宏观的高度来看要解的不等式，实际上是已知一个函数的两个函数值的大小关系，来确定它们所对应的两个自变量的值的大小关系，者可以利用函数的单调性来解决。

解：∵f(x)是奇函数，且在上是增函数，上是增函数.又不等式

（三）整体思想在几何中的应用

1.在平面几何中的应用

在解决几何问题时，尤其是不规则的图形时，往往会利用到整体补形思想.整体补形思想指的是依照已知的图形，将不规则的图形简单的拼接成规则的完整图形，从而达到简化问题的目的.整体补形时一般会将原图补成一些常见的规则图形，如：等边三角形、正方形、长方形、等腰梯形等。

2.在立体几何中的应用

整体补形思想不仅适用于平面几何问题，其同样适用于立体几何问题，对基本图形整体理解，将不规则图形补成规则图形，更方便解题。

3.在解析几何中的应用

在解决有关直线和圆锥曲线问题时，常利用整体思想，整体变形，设而不求等方法，可避免求交点等复杂计算，从而更加简洁明了的求出问题。

三、结束语

综上可得，整体思想可用于代数化简求值，解析几何，三角函数等多个方面。在遇到有关类似的数学问题时，要不拘泥于细节，要从全局着眼考虑问题，熟练掌握整体思想解题的策略,如整体换元，整体变形，整体约简，整体构造等，使得问题得以明朗花。希望本文能使大家找到解题的思路和方法，多加练习，为学习其他知识奠定良好的基础。