Dynamic mechanical behaviors of high-nitrogen austenitic stainless steel under high temperature and its constitutive model
WANG Yanli, JIA Guzhai, ZHANG Ting, WAN Mingming, JI Wei, MU Xiaoming
(No. 52 Institute of China Ordnance Industries, Yantai 264003, Shandong, China)
High-nitrogen austenitic stainless steels (HNS) are becoming important engineering materials. Their excellent properties, such as high strength, ductility, toughness and work hardening, non-magnetism, good corrosion resistance and reduced tendency to grain boundary sensitization are of great interest for sea water systems, chemical and nuclear industries, and military application[1]. As a potential armor protective material, High-nitrogen stainless steels will suffer from various dynamic loads such as explosive blast or projectile impact. In the process of projectile impact, the materials will endure high strain rates and high temperatures. In these conditions, the mechanical properties of materials could be different from quasi-static mechanical properties. Therefore, it is significant to find out about the mechanical behaviors of HNS in both low and high rates deformation processes.
Investigations of HNS’s mechanical behavior have been carried out for many years, and some achievements have been made. Tomotaetal.[2]discovered a trans-granular cleavags like fracture facet in Cr-Mn-N austenitic stainless steels, which is a totally different fracture mechanism. Speideletal.[3]studied the dynamic mechanical behavior of high-nitrogen steel by ballistic tests, and the results show that the material’s strength increases strongly under high strain rate impact. The material exhibits an obvious impact hardening phenomenon in the projectile impact area, which can enhence its protection capability obviously. Frechardetal.[1]discovered that B66 high-nitrogen steel has high-strain hardening rate, good ductility and great rate sensitivity. They also studied the temperature sensitivity of the material over a large temperature range from 77 K to 673 K. Pengetal.[4]studied two kinds of high-nitrogen steels (air cooling and water cooling separately), and found that the flow stresses of two materials are much sensitive to the strain rate. The materials present the strain hardening behaviors, but the dynamic yield stress of the materials has relatively weak strain rate sensitivity. Chenetal.[5]studied the ballistic capability of high-nitrogen steel plates (with the mass fraction of nitrogen of 0.56%) of various thicknesses, and found that the impact hardening behaviors of the material is obvious, and the material has shown excellent protection capability. But up to now, few studies are documented on the dynamic mechanical behavior and constitutive relation of HNS under high temperature tests.
In this study, dynamic tensile tests were performed to investigate the deformation behavior of HNS over a large range of strain rates and temperatures. The sensitivities of HNS to temperature and strain rate are investigated, and a modified Johnson-Cook constitutive model of HNS was established.
1 Experimental procedure
1.1 Material
The high-nitrogen austenitic stainless steel used in this study was manufactured byBeijingIron&SteelResearchAcademy. The nominal chemical composition of as-received ingots is shown in Table 1. The as-received material was supplied as plates of 20 mm thickness.

表1 实验用高氮奥氏体不锈钢的主要化学成分Table 1 Chemical composition of the as-received high-nitrogen austenitic stainless steel
1.2 Tests
Quasi-static tensile tests were performed on a material test system (MTS) at deformation rates of 0.5, 2, 5, 20, 40 and 60 mm/min, respectively. Quasi-static tensile properties of HNS were measured on two kinds of smooth cylindrical specimens, with diameter 10mm-gauge length 70 mm and diameter 4mm-gauge length 30 mm, respectively.
Dynamic tests were carried out at the strain rates of 102-103s-1by using a split Hopkinson tension bar equipment (SHTB)[6-8]. The illustraiton of the SHTB equipment is shown in Fig.1. The equipment consists of a gas gun, an incident bar, a transmitted bar, a striker, a buffer bar, a shock absorber, and strain gauge circuits to measure the strain signals in the bars. In the tests, the gas gun launches the tubular striker to impact the incident bar. The transfer flange transfers the incoming elastic compressive stress wave into the elastic tensile stress, which then travels through the incident bar toward the specimen. When the tensile stress wave propagates to the interface between the bar and the specimen, part of the wave is transmitted through the transmission bar as a tensile wave, and the rest is reflected back to the incident bar as a compressive wave. The stress wave reverberates in the specimen until a nominally homogeneous stress state is achieved. The strain signals were transferred into electrical signals by high dynamic strain indicator; the electrical signals were recorded by the multi-channel transient digital recorder.
For the temperature testing, the specimens were enclosed in a clamshell radiant-heating furnace with an internal diameter of 100 mm and with a heating wire of 500 mm in length. The specimen’s temperature was monitored by a thermocouple placed inside the furnace and contacted with the specimen’s surface. A variable transformer was used to control the temperature of the furnace. In order to reduce the temperature’s influence on the strain gauges, a circulating water device was used to cool the ends of the bar which is heated.
2 Results and discussion
2.1 Effects of strain rate
True stress-strain curves of HNS obtained from tensile tests at various strain rates under room temperature are presented in Fig.2. The curves show nearly the same flow-stress trend for both dynamic tests and quasi-static tests. But the strain hardening is more evident in the quasi-static tests than that in the dynamic tests. At high strain rate, the flow stress increases little as the plastic strain increases; the curve is nearly parallel to the strain axis when the strain rate exceeds 103s-1. It also shows that, as the strain rate increases, the flow stress increases accordingly. The dynamic curves show a distinct strain rate effect on the flow stress compared with the quasi-static curves. The yield stress is about 857.1 MPa at the strain rate 4.8×10-3s-1, and the Young’s modulus of HNS is 204 GPa. The flow stress level at high strain rate is about 500 MPa higher than that obtained at low strain rate.
Since the stress-strain curves from the dynamic tests show no evident yield platform and it is not accurate enough for their elastic sections, it is not easy to locate the yield point in a curve directly. In this study, two straight lines were used to assign the yield point, one fitted with the plastic section of the stress-strain curve, and the other plotted at strain of 0.2%, the slope of which is the value of HNS’s Young’s modulus (204 GPa). The stress value of the cross point of the two straight lines was defined as the yield stress. This method is shown in Fig.3.
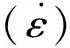
It can be seen that the dynamic strain rate sensitivity is higher than the low strain rate sensitivity. This difference in slope implies that different deformation mechanisms govern in these two ranges. The dominant rate-controlling mechanism is thermally activated at low strain rate and it tends towards a dislocation of viscous damping when the strain rate increases continuously.
2.2 Effects of temperature
Fig.5 shows the curves of true stress via true strain at various temperatures from 293 K to 873 K, at the same striker driving-pressure (1.3 MPa). It also gives the values of strain rates corresponding to the tests at each temperature. It shows that as the temperature increases, the strain rate increases as well though under the same driving-pressure. That is caused by the high deformation rate in dynamic tests at high temperature. Thus, for the dynamic tests under high temperatures, the deformation behavior of the material is influenced simultaneously by both strain rate and temperature.
The yield stress of each test at high temperature was obtained by using the same method introduced in Chapeter 2.1. Fig.6 presents the influence of strain rate and temperature on yield stress. The projections of data points on the vertical coordinate plane were acquired. From that, the yield stress increases rapidly with the decreasing of temperature. it means that the thermal softening effect plays a key role in the dynamic deformation process in high temperature tests. Namely, the strain rate hardening effect was very weak in these conditions because all the high temperature tests were under the same striker driving-pressure, and the changes of strain rates of the tests were not much. It can be inferred that, over a large range of strain rate and temperature, the material’s deforming mechanism was dominated by the competitive relation between the thermal softening effect and the strain rate hardening effect.
2.3 Constitutive model
The Johnson-Cook model relates the three mechanisms, i.e. the work hardening, the strain rate hardening, and the thermal softening, that are responsible for the deformation behavior of materials. The main advantage of this model is that, it is relatively easy to correlate with the minimum of experimental data in the form of stress-strain curves at different strain rates and temperatures. The Johnson-Cook model assumes that the slope of the flow stress curve is independently affected by strain hardening, strain rate hardening, and thermal softening behaviors[9]and the law is given as
(1)
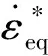
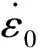
Fig.7 gives the plots of the influence of strain rate on the yield stress, and the fitted curve by the Johnson-Cook model. The value of the parameterCis obtained as 0.046. From Fig.7, it can be seen that the Johnson-Cook model cannot be fitted with the test data very well, because the material has different sensitivities at low strain rates and high strain rates. In this study, a modified model was used, the data obtained from low strain rate tests and high strain rate tests were fitted separately by two straight lines. The parametersC1=0.021 andC2=0.318 were used to represent the slopes of the two straight line respectively.
From Chapter 2.2, it can be known that, the deformation behavior of the material is influenced by strain rate and temperature simultaneously in the dynamic tests under high temperatures. Thus, the yield stress, which acquired directly from test data, contains the effect of strain rate, though the strain rate of the tests were not much different. In the Johnson-Cook model, it is assumed that the slope of the flow stress curve is independently affected by the strain hardening, the strain rate hardening, and the thermal softening behaviors. Thus the yield stress, influenced by temperature, can be obtained by using the Johnson-Cook model to uncouple the strain rate effect. Fig.8 plots the influence of dimensionless temperature on yield stress. By fitting the data withσeq=A(1-T*m), the parameterm=0.55 is obtained.
In this study, the yield stress data at low and intermediate strain rates were not provided, for the lacking of appropriate experimental means. The Johnson-Cook model of HNS obtained above, which described the mechanical behavior at quasi-static and high strain rate, can help predict the flow behavior of HNS under low and intermediate strain rate range.
2.4 Verification of constitutive model
The Johnson-Cook model of HNS was obtained by correlating the tests data, which contains two expressions at different strain rates. The modified Johnson-Cook model is given as follows:
(2)
By comparing the equivalent stress-strain curve from the tests with the modified Johnson-Cook model, the accuracy of the model can be verified. Fig.9 shows the test curves at different strain rates at room temperature and the relevant curves obtained from the modified Johnson-Cook model. In the Johnson-Cook model, the necking phenomenon is not taken into account, thus only the comparison of the curves before necking makes sense. It is noted that the model presicts well about the test results when the strain rate is below 103s-1. As the strain rate inceases, there is obvious high frequency oscillation in the test curves, which is caused by the screw connection between the specimen and the Hopkinson bars. It causes the flow stress value of the curves’ initial part higher than the predicted value from the model. Fig.10 plots the curves of tests at high temperatures and the relevant curves obtained from the modified Johnson-Cook model. It can be seen that the modified model can predict the material’s dynamic mechanical behavior at high temperature very well.
Generally the modified Johnson-Cook model can describe the dynamic mechanical behavior of HNS properly.
3 Conclusion
It has been shown that the flow stress of HNS is strongly influenced by strain rate and temperature. This material exhibits a great strain rate hardening effect, and its sensitivity at high strain rates is much higher than that at low strain rates. The thermal softening effect seems to be a key role than strain rate hardening effect in dynamic tests at high temperature. The modified Johnson-Cook model of HNS was obtained. Verified with test data, this model describes the observed flow behavior of HNS quite satisfactorily.
Reference
[1] FRECHARD S, REDJAIMIA A. Dynamical behaviour and microstructural evolution of a nitrogen-alloyed austenitic stainless steel[J]. Materials Science & Engineering, 2008,480(2008):89-95. DOI: 10.1016/j.msea.2007.07.014.
[2] TOMOTA Y, NAKANO J, XIA Y, et al. Unusual strain rate dependence of low temperature fracture behavior in high nitrogen bearing austenitic steels[J]. Acta Materialia, 1998,46(9):3099-3108. DOI: 10.1016/S1359-6454(98)00005-6.
[3] SPEIDEL M O, KOWANDA C, DIENER M. High nitrogen steel 2003[M]. Swiss: Institute of Metallurgy, 2003:63.
[4] PENG X. Dynamic pressure tests and constitution relation of high-nitrogen alloy steel[D]. Chengdu: Southwest Jiaotong University, 2009:23-38.
[5] 陈巍,刘燕林,齐志望,等.高氮奥氏体装甲钢抗弹性能研究[J].兵器材料科学与工程,2009,32(6):51-55.
CHEN Wei, LIU Yanlin, QI Zhiwang, et al. Research on ballistic behavior of high nitrogen austenitic armor steel[J]. Ordnance Material Science and Engineering, 2009,32(6):51-55.
[6] GRAY G T. High-strain-rate testing of materials: the split-Hopkinson pressure bar[M]. 2nd ed. New York: John Wiley Press, 2000:96-110. DOI: 10.1002/0471266965.com023.
[7] NICHOLAS T. Tensile testing of materials at high rates of strain[J]. Experimental Mechanics, 1981,21(5):177-185. DOI: 10.1007/BF02326644.
[8] TANG X, PRAKASH V, LEWANDOWSKI J. Dynamic tensile deformation of aluminum alloy 6061-T6 and 6061-OA[J]. Journal of Experimental Mechanics, 2007,22(3/4):305-313.
[9] OWOLABI G, ODOH D, ODESHI A, ET AL. Occurrence of dynamic shear bands in AISI 4340 steel under impact loads[J]. World Journal of Mechanics, 2013,211(3):139-145. DOI: 10.4236/wjm.2013.32011.

