Transverse Transport of Polymeric Nano fluid under Pure Internal Heating:Keller Box Algorithm
R.Mehmood,S.Rana,and E.N.Maraj
Department of Mathematics,Faculty of Natural Sciences,HITEC University,Taxila Cantt,Pakistan
Nomenclature
1 Introduction
Non-Newtonian fluids in recent times have achieved extensive position in numerous aspects of science,engineering and technology mostly in substantial dispensation,natural and atomic productions,geophysics,and bio-engineering. These fluids display a recipe of viscid and flexible conduct under strain.The characteristics of all these types of non-Newtonian fluids are described by highly non-linear constitutive equations.In fact,Navier-Stokes theory does not cover all rheological properties of complicated fluids like polymer solutions,blood,paints,certain oils,greases etc.Major difficulty of non-Newtonian fluids is the presence of non-linearity,which cannot be handled by traditional constitutive relation for all fluids.[1]The discussion of Non-Newtonian fluids is of substantial concentration in lubricant reservoir manufacturing.The role of viscosity in a linear stress strain equation leads to be a fluid as Newtonian/non-Newtonian.There are some non-Newtonian second order fluids,like a convected Maxwell fluid,and an Oldroyd A and B fluids.Numerous fluid models are suggested by many researchers in the history of fluid mechanics,which are mainly divided into three classes’rate type,differential type,and integral type.In modern ages,the Oldroyd-B fluid has learnt a distinct grade midst the countless fluids of the rate type.Oldroyd-B type fluid is one of the simplest constitutive models that describe the viscoelastic conduct under general flow circumstances.
Mehmood et al.[2]gave theoretical study of micropolar second grade fluid heat transfer properties.Nadeem et al.[3−4]investigated flow of nanoparticle for third grade fluid with heat transfer characteristics and studied second grade nanofluid for thermophertic and Brownian motion effects.Rahman et al.[5]studied the properties of thermophertic parameter and Brownian motion parameter for oblique laminar flow of viscid nanofluid.The study of different physical features of stagnation point flows towards a stretched sheet has attracted numerous researchers.[6−8]Crane[9]considered flow over a linear stretched sheet.Cortell[10]discussed stretching flow along with heat transmission.
Heat transfer phenomena are of vital importance in fluid mechanics now days.Pohlhausen[11]examined heat transfer problem with assuming uniform temperature at the plate.Aziz[12]and Magyari[13]studied similar type of problem with convective boundary condition.Ishak[14]used Aziz’s problem for suction/injection on levelled surface.Haddad et al.[15]studied analytically the nanofluid based on Rayleigh-Bernard problem,he made comparison for presence and no presence of Brownian motion and Thermopherotic effects.Nadeem et al.[16]numerically investigated the heat and nanofluid flow properties of Oldroyd-B type fluid on a stretched sheet.Sheikholeslami et al.[17]studied effects of MHD and natural convection of water based nanofluid with consideration of Brownian motion and Thermopherotic effects.Sheikholeslami et al.[18]significantly discussed the influence of Brownian motion and Thermopherotic constraints on nanofluid flows with aid of two phase model,also effects of thermal radiation and magneto hydrodynamics are taken into account.Seth et al.[19]studied the laminar flow of viscoelastic fluid under the influence of thermal and nanoparticle buoyancy forces,in which they used convective boundary conditions for heat transfer effects.Reddy et al.[20]investigated micropolar liquid for its Thermopherotic effects on heat and mass transfer with internal heat generation/absorptions effects.Rashad et al.[21]discussed fluid passing an upright rotating cone on preamble surface for its effects of thermophertic and thermal radiation with heat and mass transfer.Some recent studies on current topic may be found in Refs.[22–41].The present study is conducted to examine oblique stream of Oldroyd-B nano- fluid past a stretched sheet with internal heat generation.The governing physical problem is solved numerically using Keller box scheme.The core outcomes of the study at summarized in the concluding remarks.To the best of our knowledge,such kind of study has not been attempted prior.The obtained results are a novel contribution,which can be benchmark for further relevant academic research related to polymer industry.
2 Formulation of the Physical Problem
Considersteady 2D incompressible flows of an Oldroyd-B nanofluid over a stretched wall with internal heat generation.To maintain equilibrium,keeping origin fixed a force is applied in horizontal direction as in Fig.1.The planar surface is stretched linearly with velocity uw.It is assumed that the fluid strikes the surface obliquely at any arbitrary angle.Moreover,it is assumed that heat transfers through convection Tffrom stretched surface.Furthermore,Cwis the nanoparticles concentration at the surface and T∞and C∞are nanofluid temperature and concentration far away from the surface.
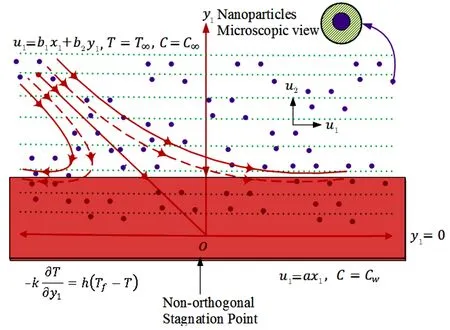
Fig.1 Geometrical description of model.
The governing equations for an Oldroyd-B nanofluid model are as follows:
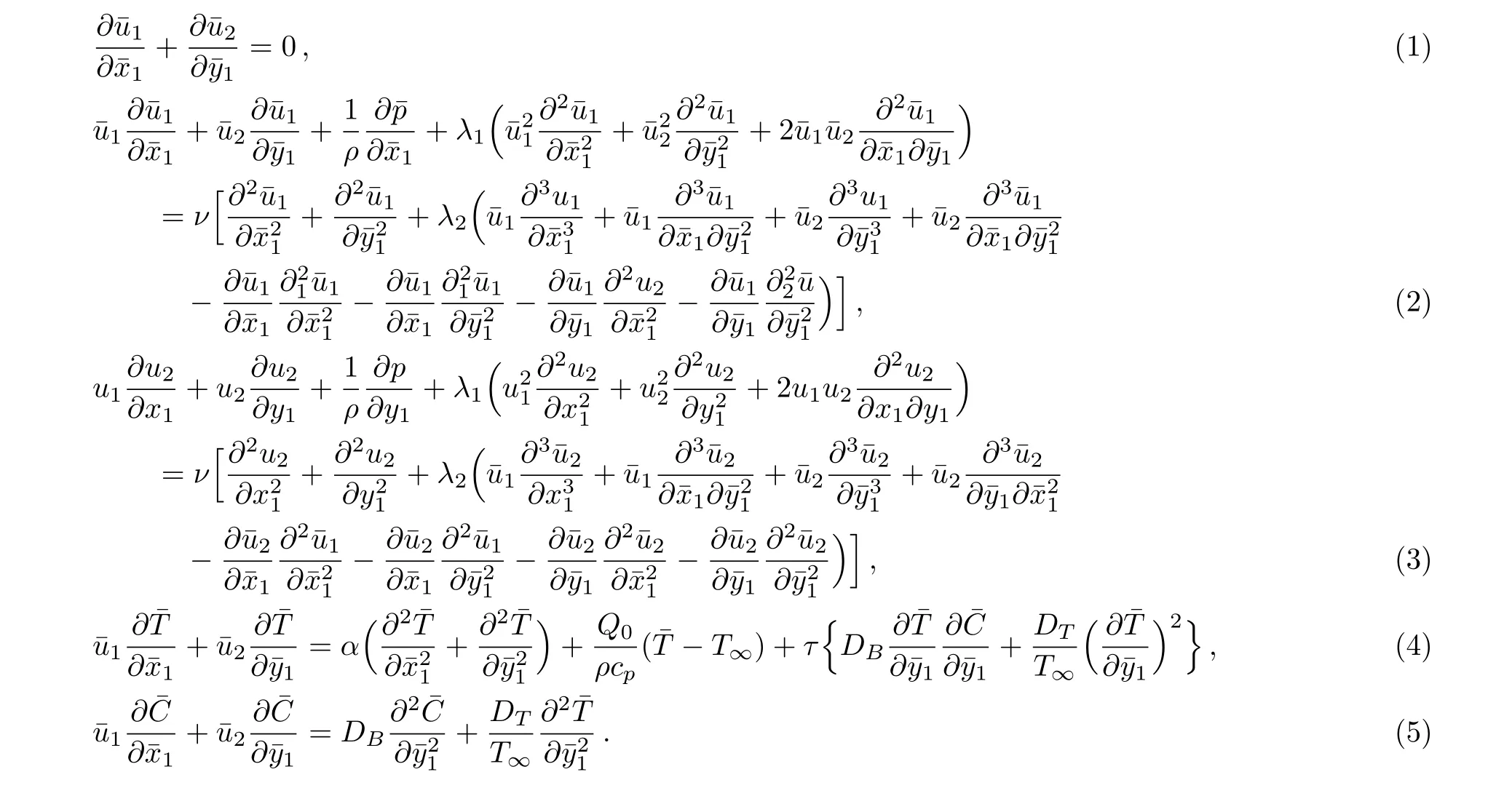
The consistent boundary conditions are[36]
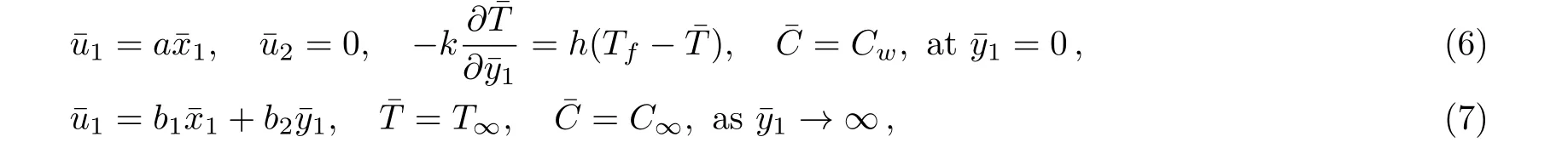
wherecomponents of velocity respectively,ν is known as kinematic viscosity,is termed as pressure,ρ is taken to be density,T¯ is termed as temperature,λ1and λ2are relaxation and retardation times,α and k are taken to be thermal diffusivity and thermal conductivity,DBis known as Brownian dispersion constant,DTis taken as Thermopherotic dispersion constant,T∞is ambient fluid temperature,Cwis nanoparticle absorption on surface,C∞is defined to be free stream nanoparticle absorption,τ is proportion of heat capacity of nanoparticle and fluid,a,b1,b2are constants.
Define following substitutions,known as scaling transformation[36]in Eqs.(1)–(7),we get

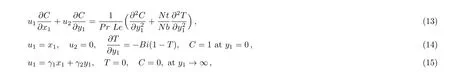
where β1= λ1a and β2= λ2a are the Deborah numbers,Pr= ν/α is Prandtl number,Le= α/DB,is Lewis number,Nt= τDT(Tf− T∞)/T∞ν is thermophoretic constraint,Nb= τD√B(Cw− C∞)/ν is Brownian motion constraint,γ =Q0/(aρcp)is heat generation/absorption constraintis Biot number, γ1=b1/a is stretching ratio,γ2=b2/a is taken as obliqueness.
Define new transformation known as stream function:[36]

Using Eq.(16)in Eqs.(9)–(15)and eliminating the pressure term,we get the following set of equations:
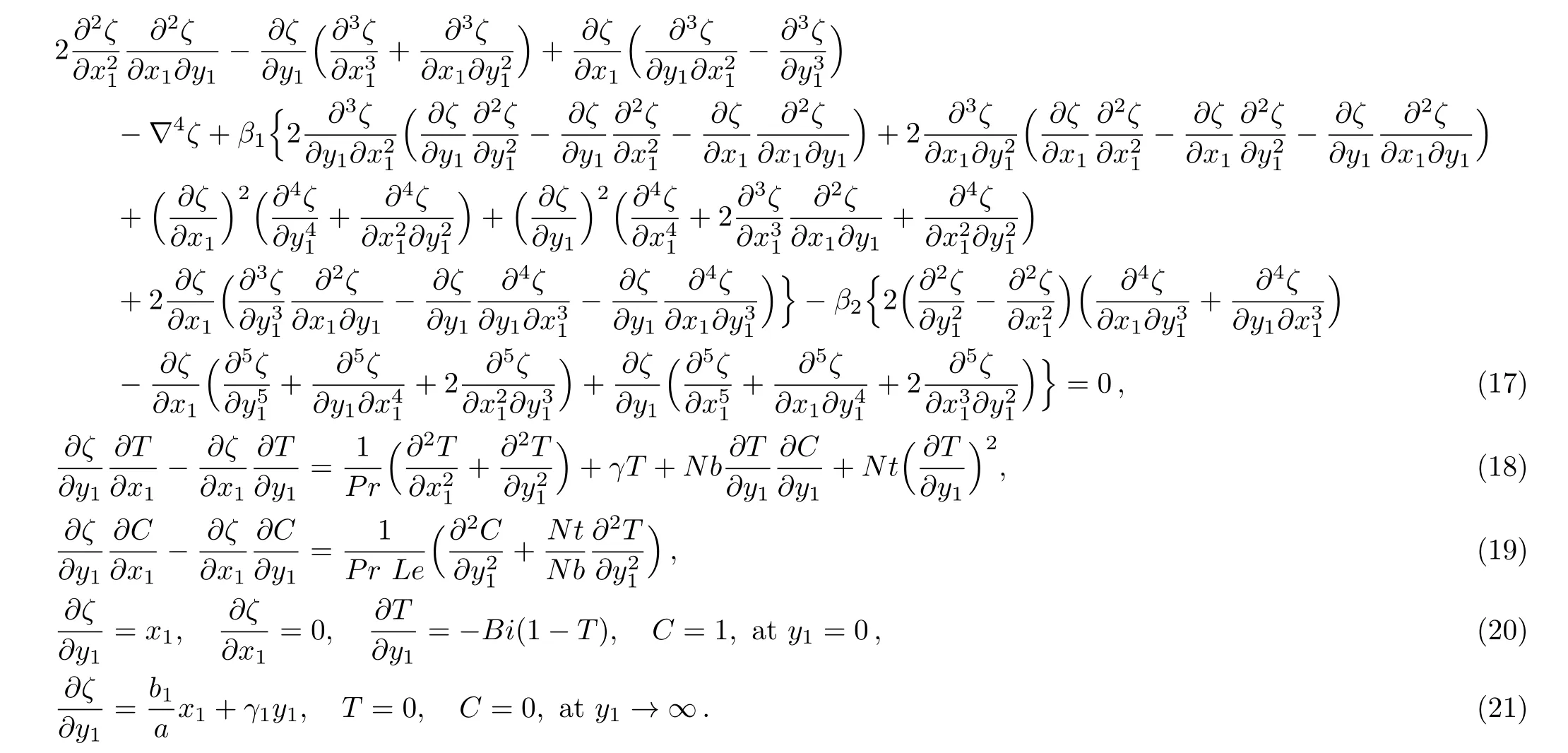
Redefining the stream function as:[36]
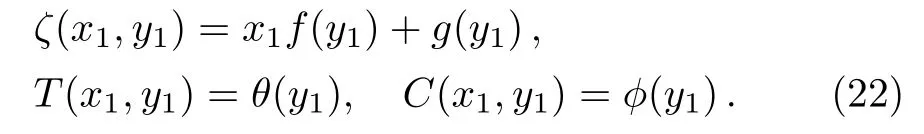
Using Eq.(22)in(17)–(21),we get,after integrating once,
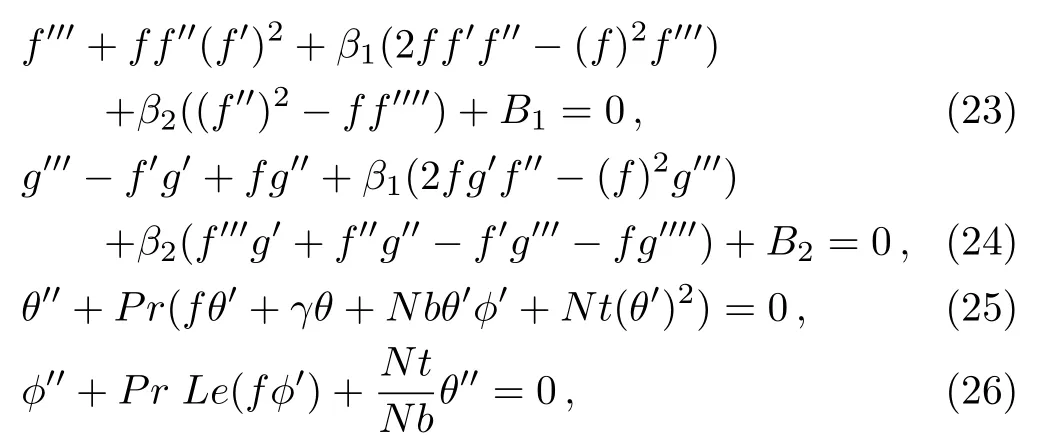
and boundary conditions(20)–(21)take the form
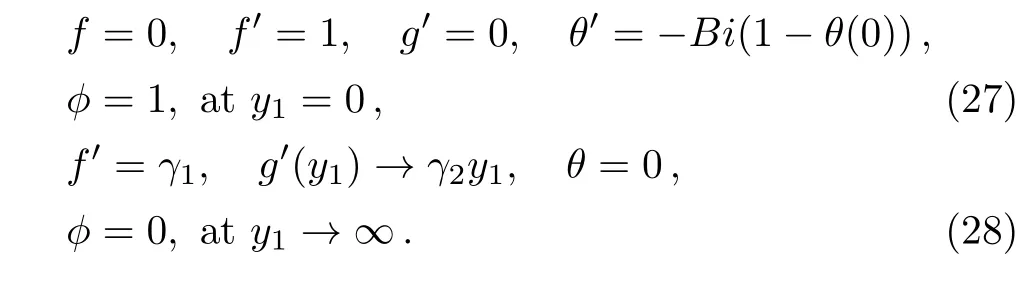
Applying the boundary conditions(28)at infinity in Eqs.(23)and(24),we get

where A is boundary layer constant.
Introducing

Using Eqs.(29)and(30),in Eqs.(23)and(24)give
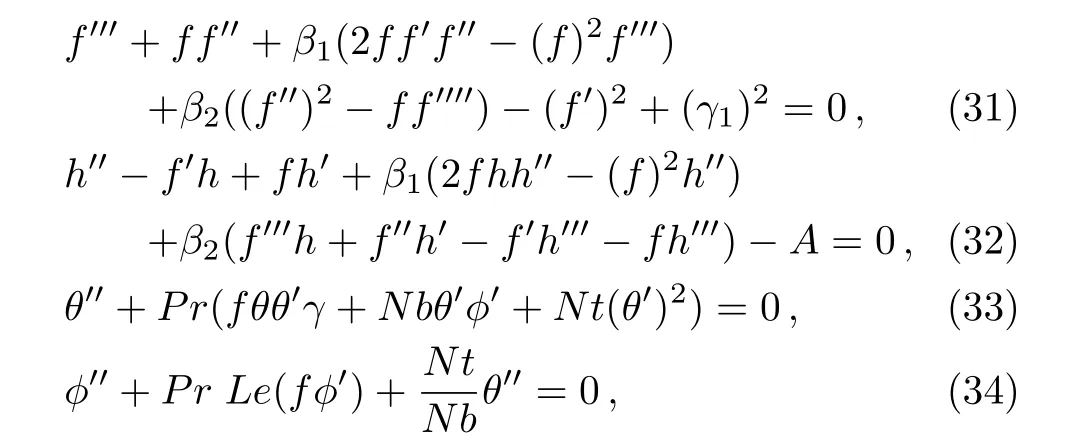
along with boundary conditions
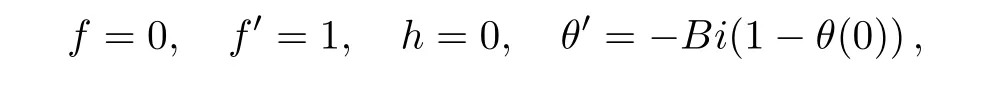
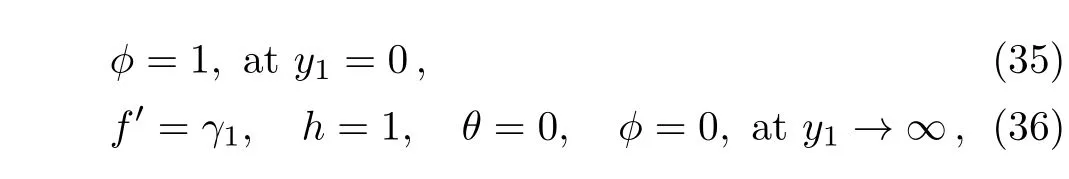
where a prime denotes derivative with respect to y1.
3 Physical Measures of Interest
Concerned physical parameters are the local heat flux and the mass flux are defined in dimensional and nondimensional form as:
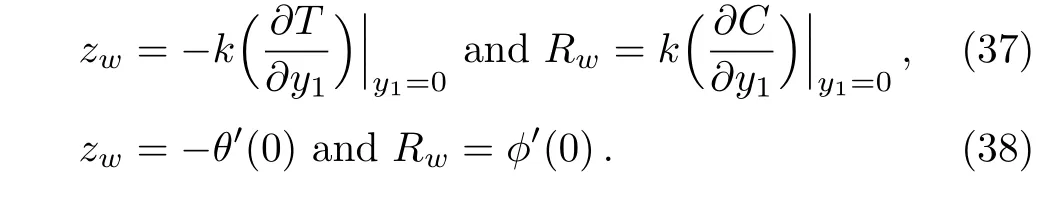
4 Numerical Solution
The system of equations(31)–(36)are reduced to system of nonlinear equations of order one by considering
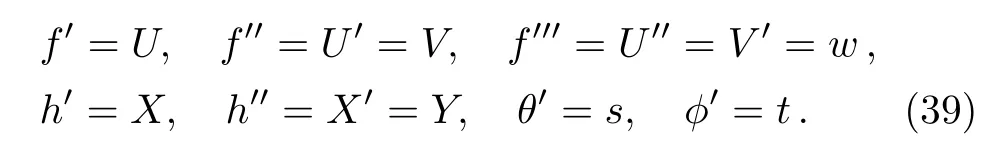
Such that Eqs.(31)–(36)become
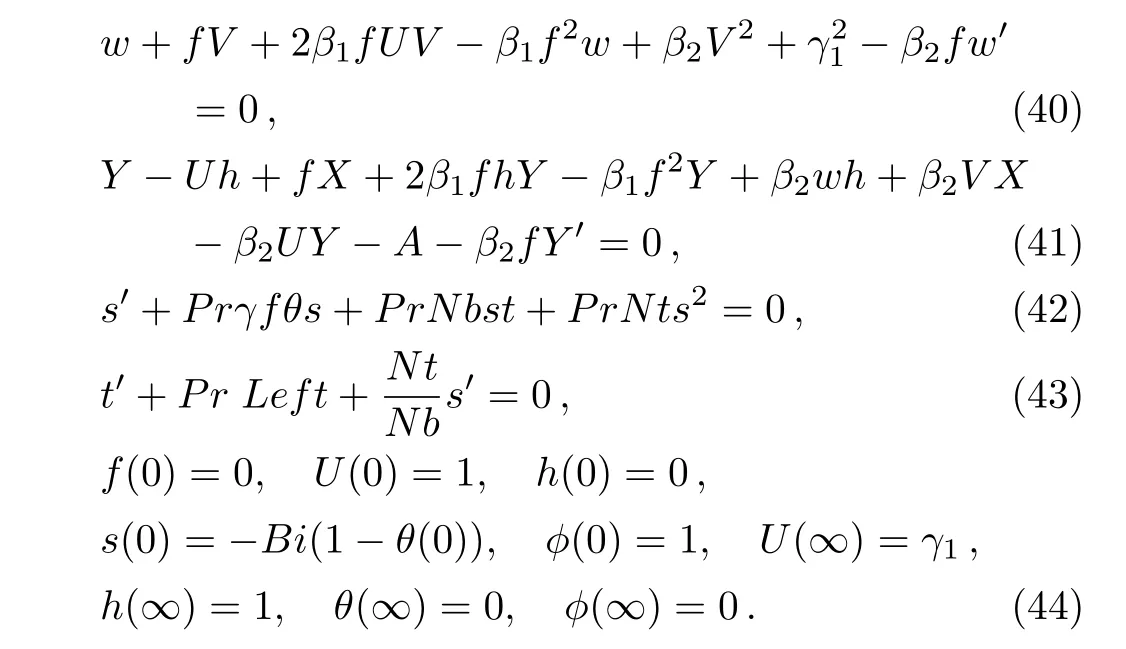
Using central difference scheme,averages centred at midpoints are
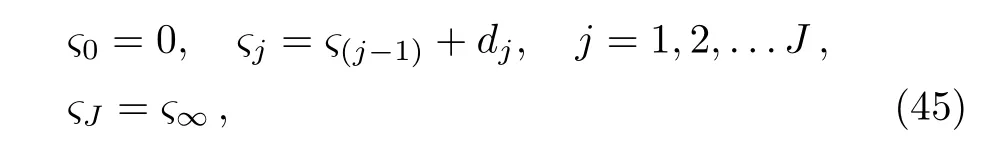
Discretized form of Eqs.(39)–(45)is
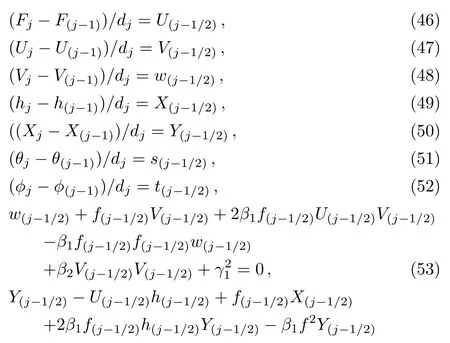
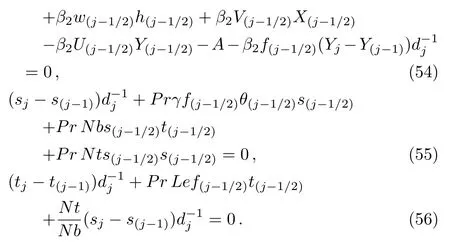
Equations(46)–(56)are nonlinear algebraic equations and can be linearized via using Newton iterations as follows:
For(i+1)-th iterates,
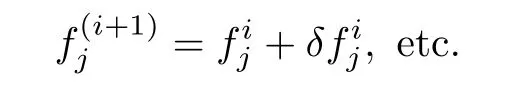
For all dependent variables,using these expressions in Eqs.(46)–(56)and neglecting higher order terms in,etc.,a linear tri-diagonal set of equations is obtained as follows:
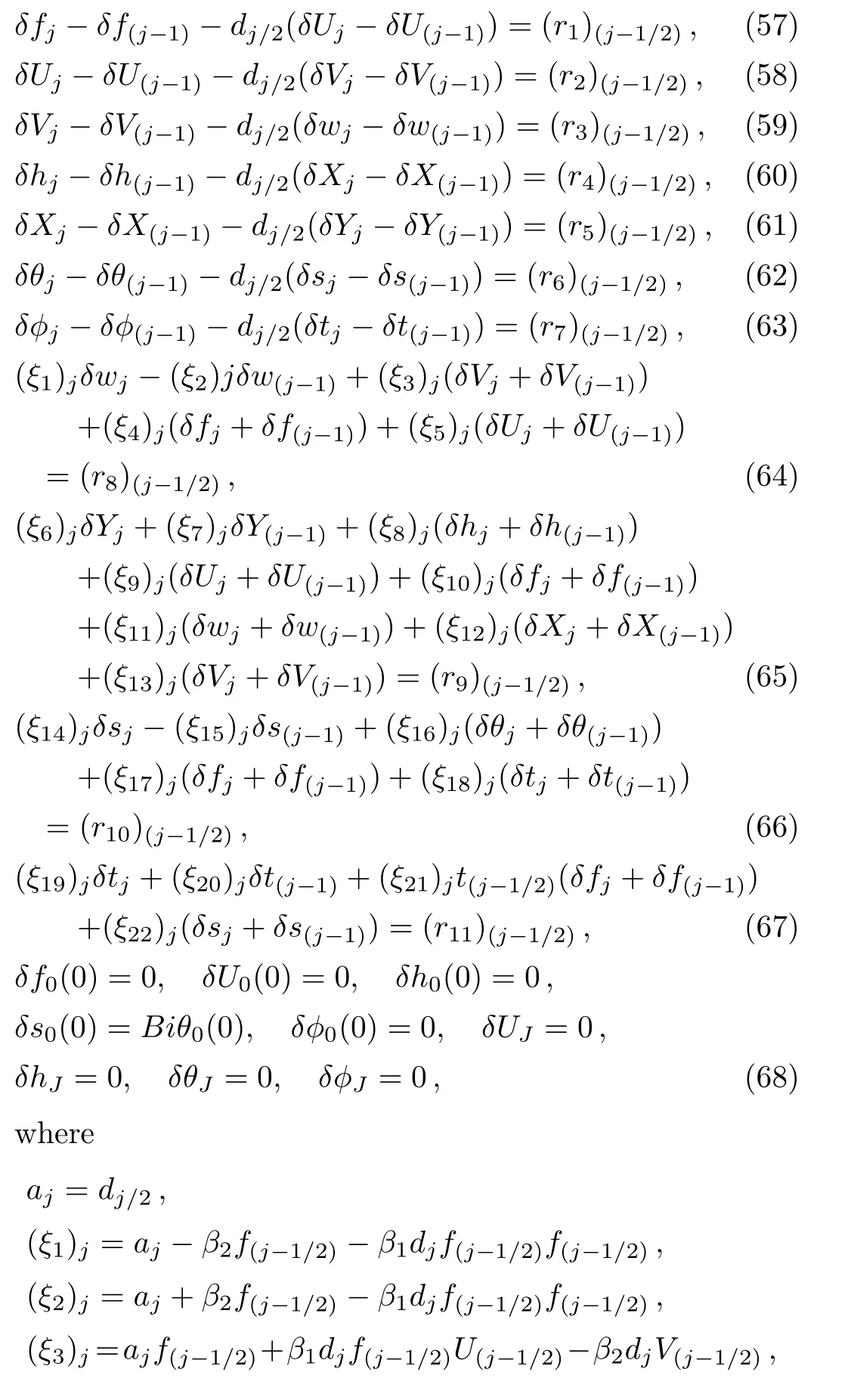
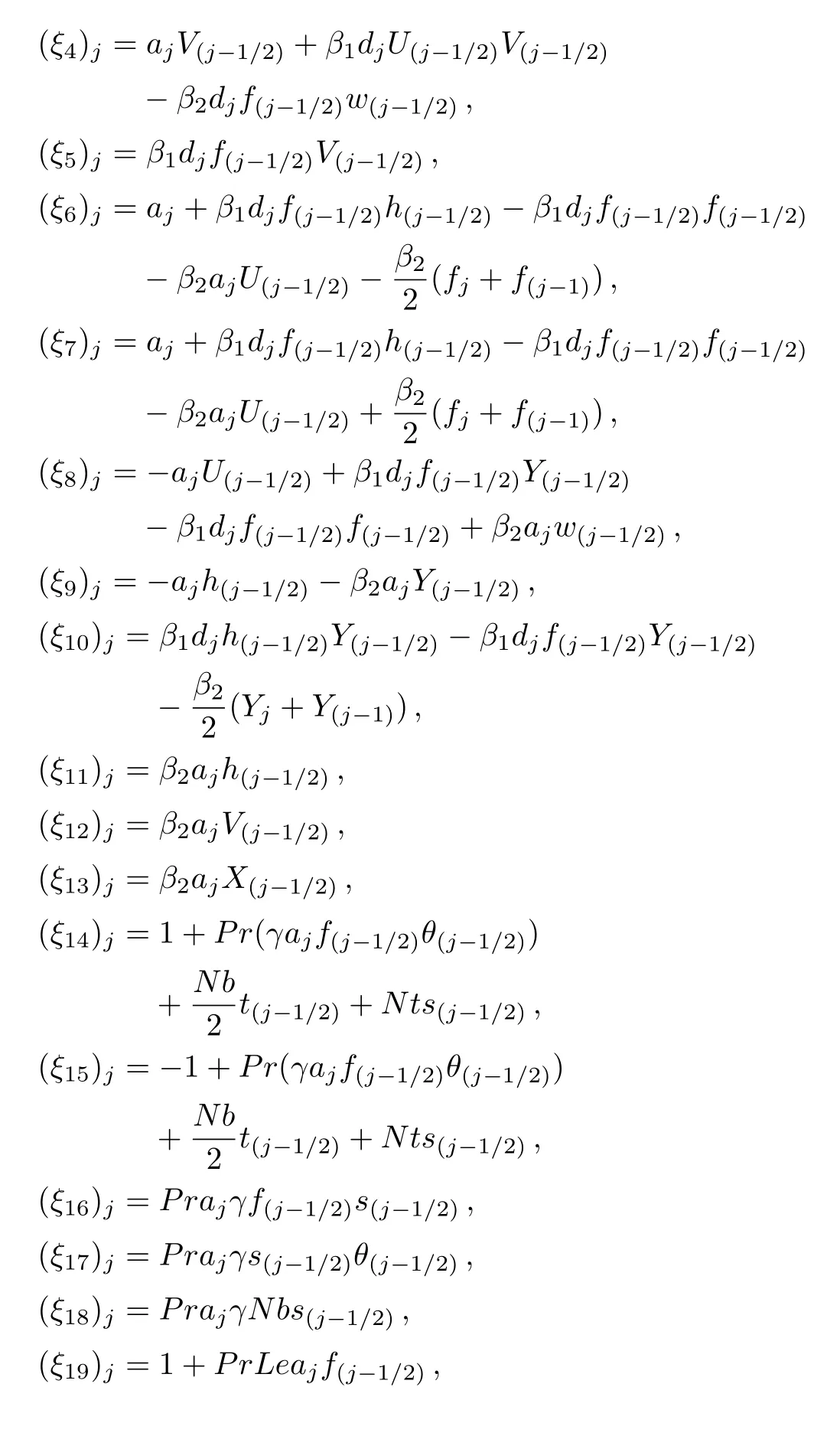
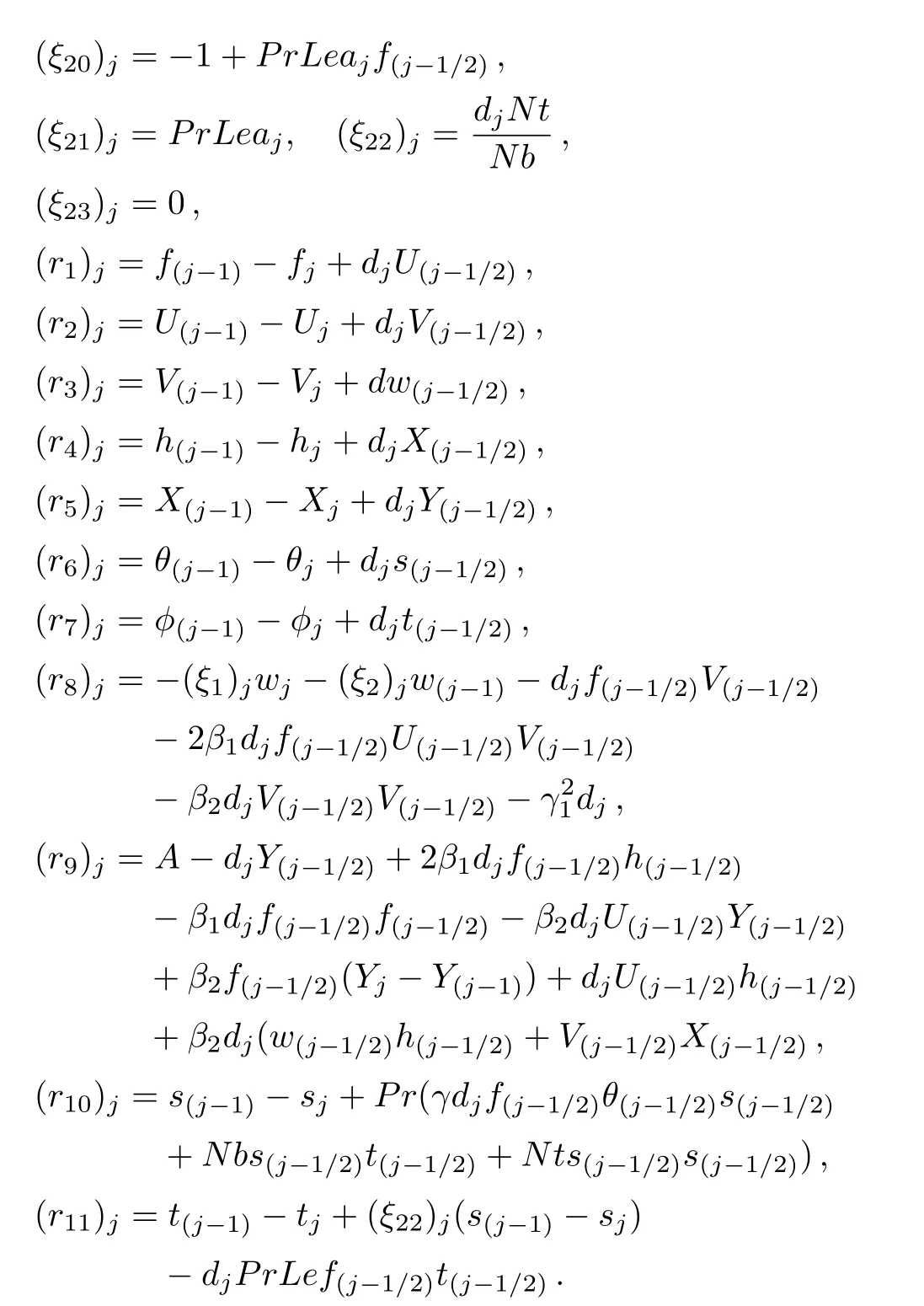
Linearized equations from Eqs.(57)–(67)can be written in vector form as:
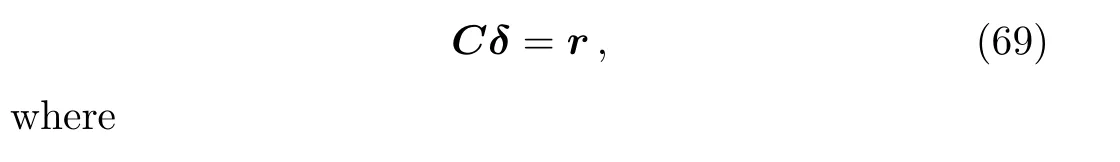


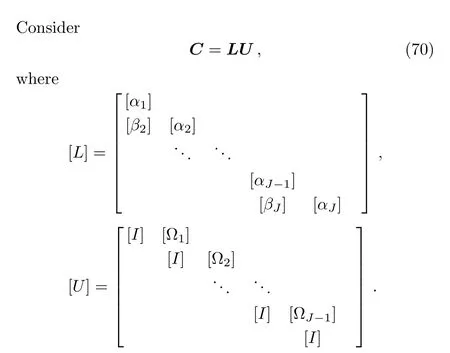
Here[I]is unit matrix and[αi],[Ωi]are square matrices of order 11 whose elements are determined by the following expressions:
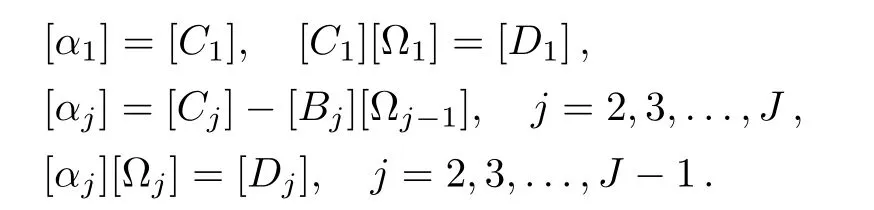
Incorporating Eq.(70)into Eq.(69),yields
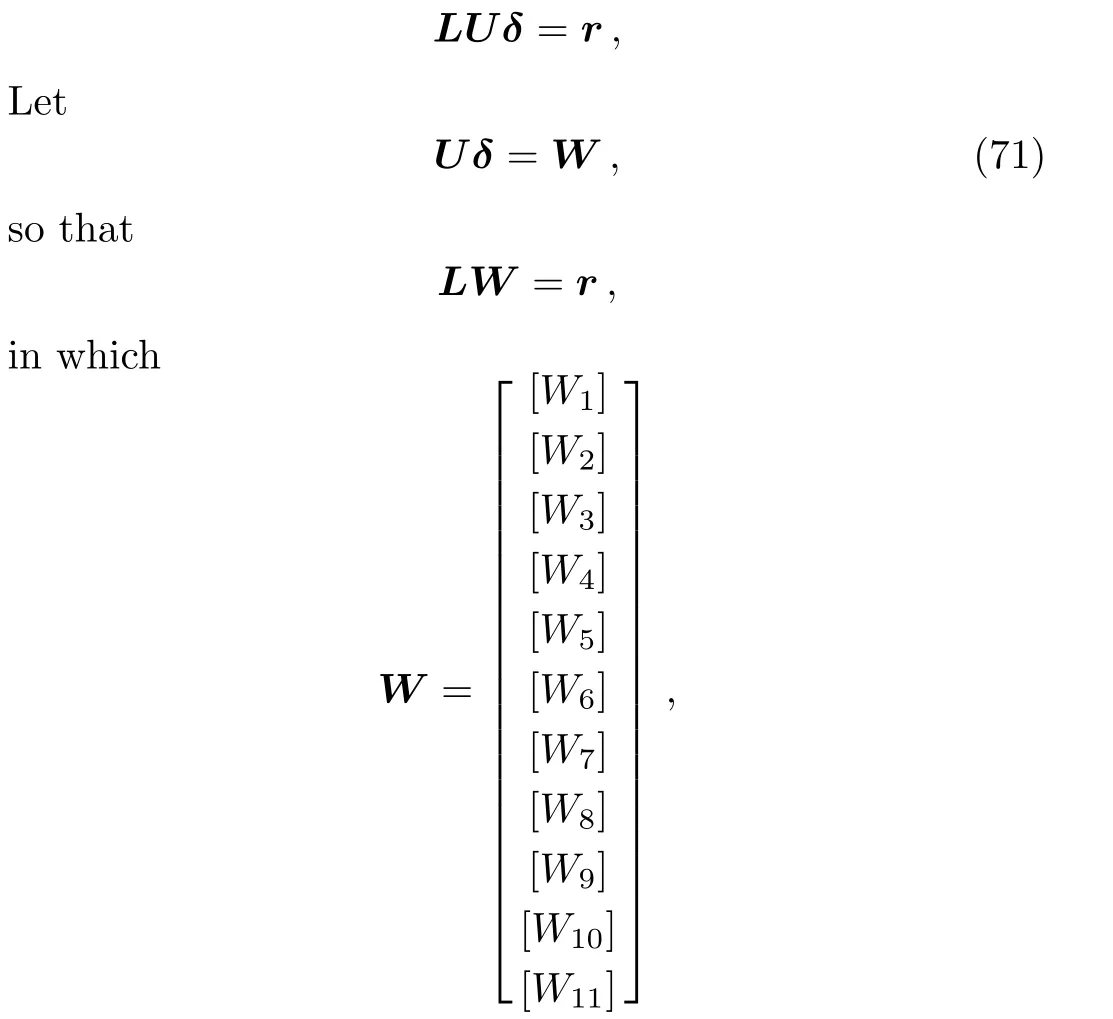
and[Wj]is a 11×1 column matrix.Elements of W are solved from following equations
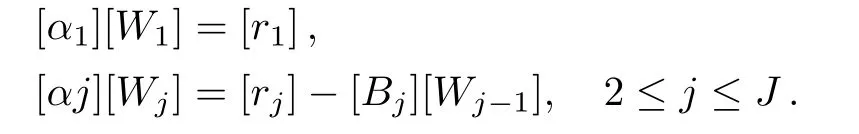
Ωj,αjand Wjare calculated by forward sweep.Once the elements of W are computed,Equation(71)gives the solution δ whose elements are obtained from following relations:
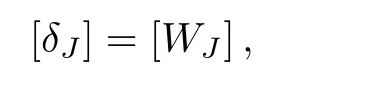
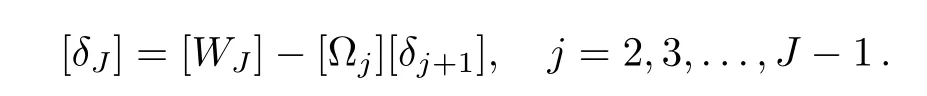
With tolerance level of 10−6calculations are carried out.
5 Results and Discussion
This section is constructed to discuss the flow of an oblique stream of Oldroyd-B nano- fluid past a stretched sheet with internal heat generation. Figures 2–23 are ploted for some fixed values of certain parameters to discuss fluid behaviour.
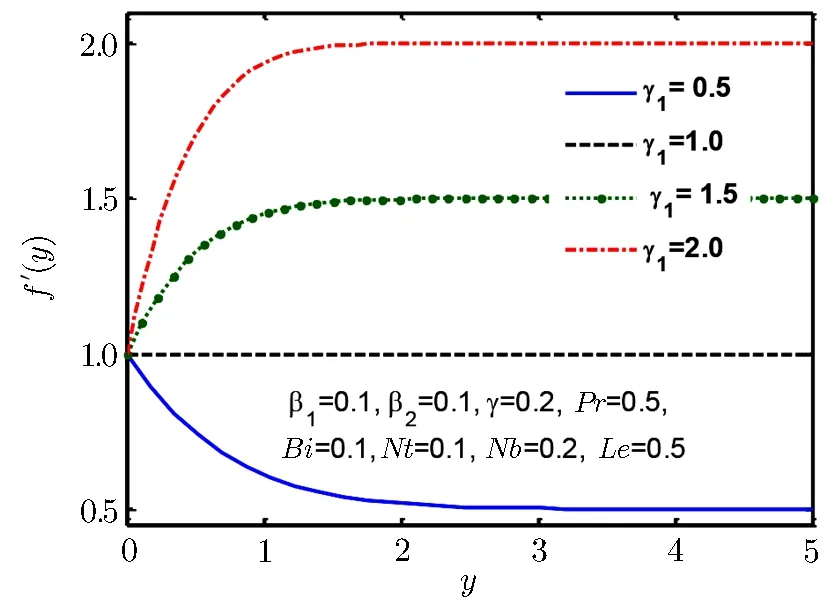
Fig.2 Velocity profile f ′(y)for γ1.
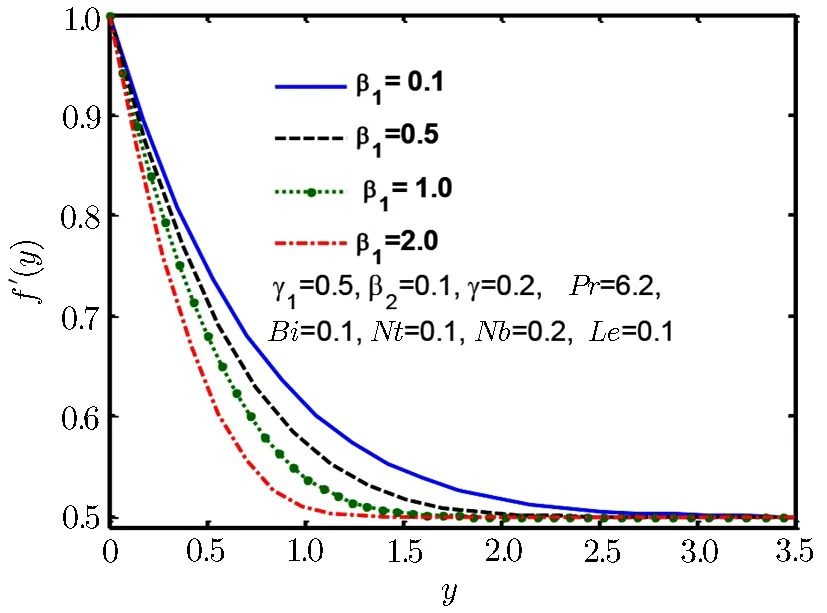
Fig.3 Velocity profile f′(y)for β1.
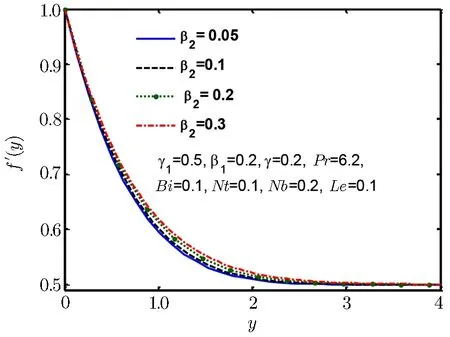
Fig.4 Velocity profile f ′(y)for β2.
We see that Fig.2 exhibits that when stretching ratio is increased then normal component of velocity also increases,further it is observed that flow has a formed boundary layer for γ1>1,moreover it is evident from this graph that flow has reversed structure for γ1<1.Physically we say that an increment in motion of liquid close to stagnated area become reason to rise in acceleration of fluid flow outside the boundary layer flow.Therefore,an increment in stretching ratio becomes reason of thinning boundary layer.Figure 3 displays behaviour of normal component of velocity as well as momentum boundary layer thickness for Deborah numbers β1.We observe that with the rise in Deborah number β1momentum boundary layer and normal velocity f′(y)declines.Normal velocity and momentum boundary layer is observed in Fig.4 for Deborah number β2which is increasing for increase in Deborah number β2.Deborah numbers β1and β2always depict the opposite reaction because of relaxation and retardation times.Physically,since Deborah number is defined as β1= λ1where λ1is relaxation time.The increment in the relaxation time leads to an increment in temperature and the thermal boundary layer thickness.Influence of β2on temperature and thermal boundary layer are opposite to that of β1,because retardation time delivers resistance which become reasons for decrease in temperature and the thermal boundary layer.
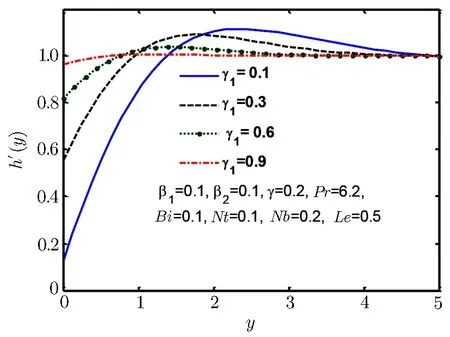
Fig.5 Velocity profile h′(y)for γ1.
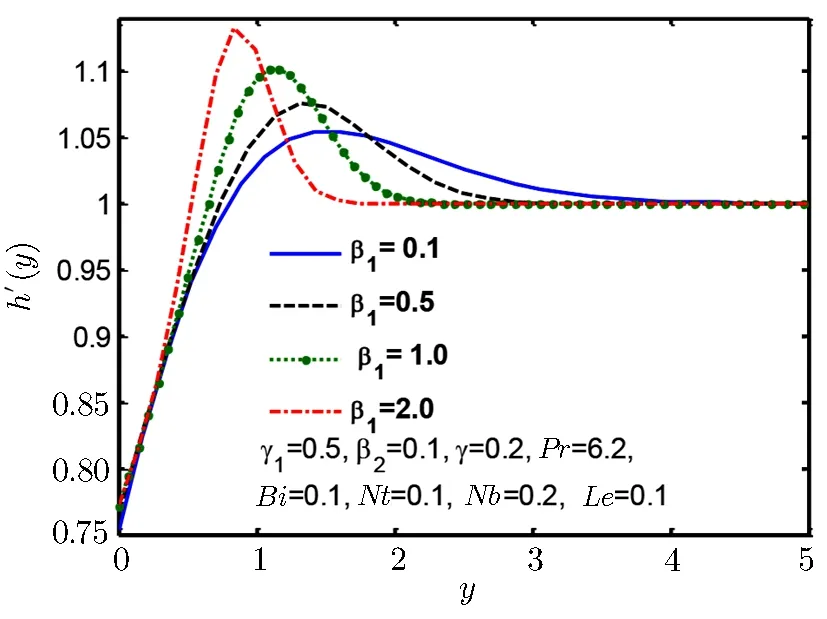
Fig.6 Velocity profile h′(y)for β1.
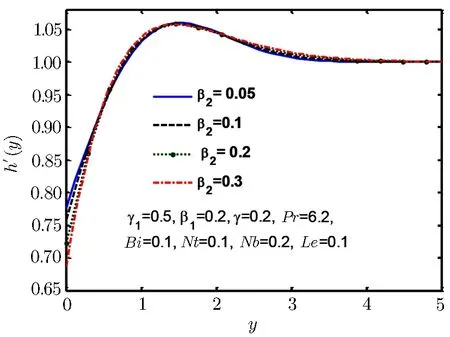
Fig.7 Velocity profile h′(y)for β2.
Figures 5–7 are plotted to show behaviour of tangential velocity for stretching ratio γ1and Deborah numbers β1and β2.For increase in stretching ratio γ1the vertical velocity h′(y)rises close to wall but reverses its behaviour as move away from wall as shown in Fig.5.Figure 6 shows similar kind of behaviour for Deborah number β1,but Fig.7 shows opposite behaviour for Deborah number β2and for increase in Deborah number β2vertical velocity h′(y)decreases near the wall but reverses its behaviour away from the wall.
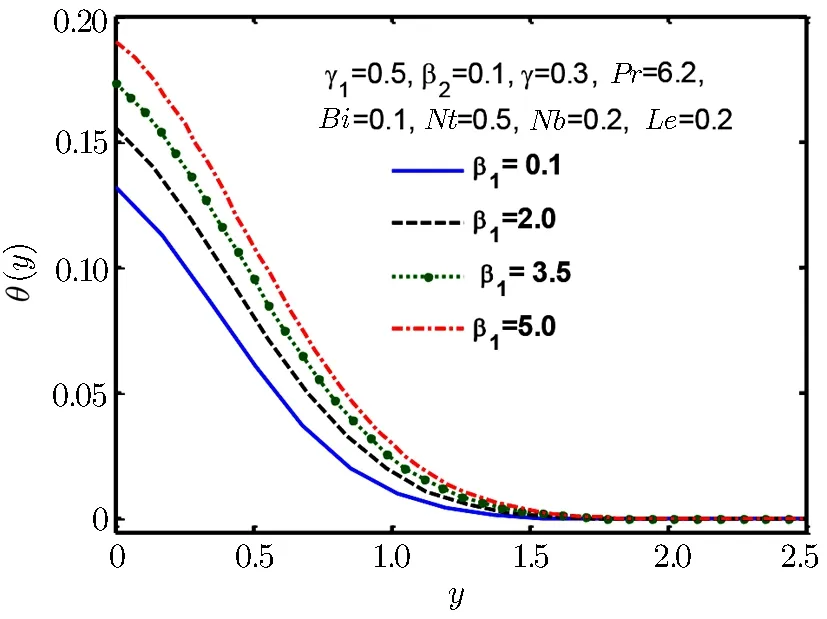
Fig.8 Temperature profile θ(y)for β1.
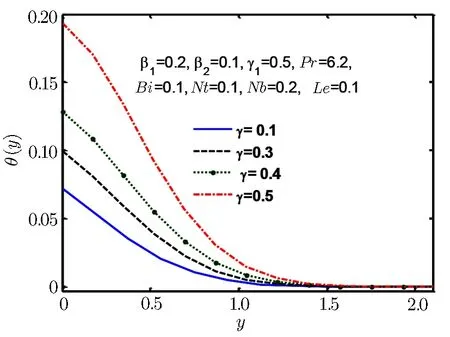
Fig.9 Temperature profile θ(y)for γ.
Figures 8–13 are plotted to show the behaviour of temperature θ(y)for Deborah number β1and heating source and sink parameter γ,Biot and Prandtl number Bi and Pr,thermpheresis parameter Nt and Brownian motion parameter Nb.From Fig.8 we find that temperature and thermal boundary layer tend to rise with a rise in Deborah number β1.In Fig.9 we observe that temperature rises for increase in γ.Prandtl number is the ratio of momentum to thermal diffusivity.Larger values of Prandtl number have higher momentum thermal diffusivity.
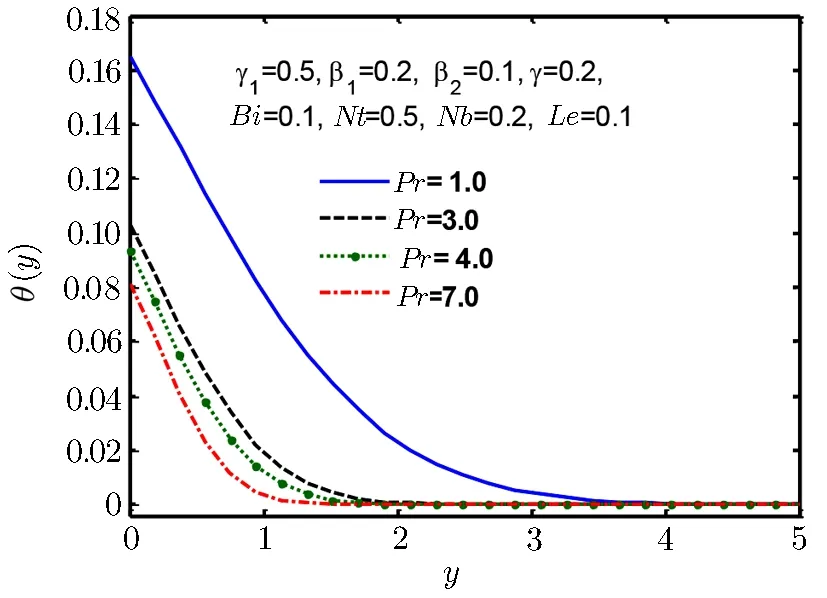
Fig.10 Temperature profile θ(y)for Pr.
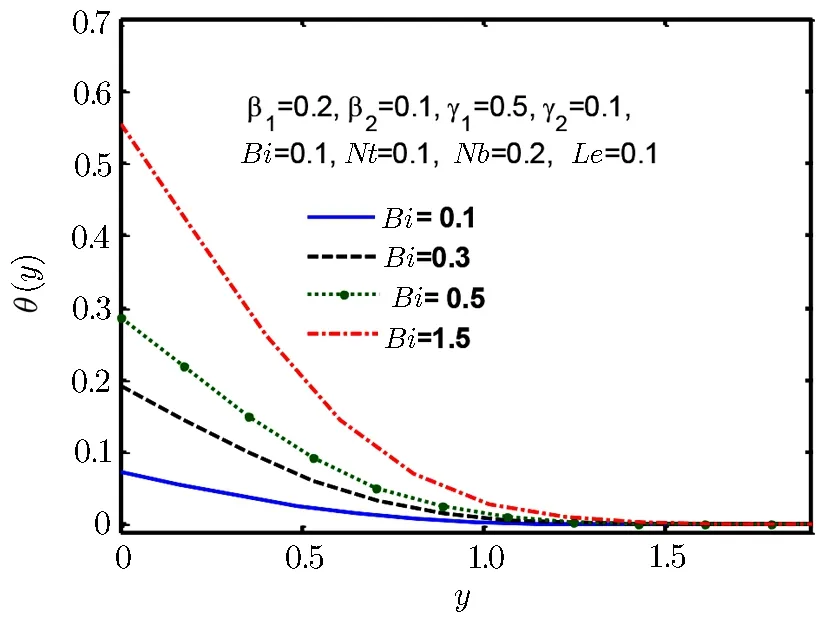
Fig.11 Temperature profile θ(y)for Bi.
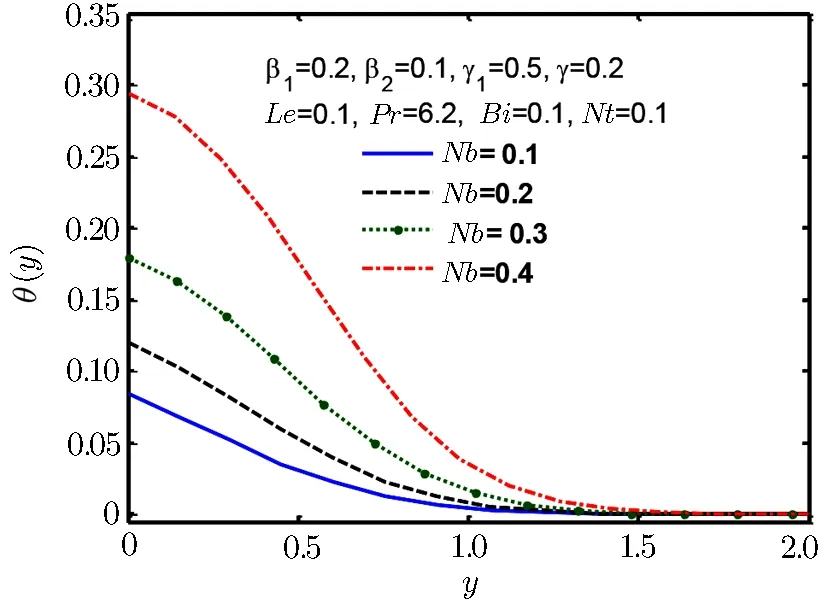
Fig.12 Temperature profile θ(y)for Nb.
It is observed in Fig.10 that for an increment in Prandtl number Pr,temperature θ(y)and thermal boundary layer tends to decline.When Prandtl number rises it implies a decline in thermal diffusivity that lead to decrease of energy transfer ability and it results in reducing the thermal boundary layer thickness.Biot number represents the ratio of internal resistive force of body,to external resistive force to heat convection.Thus,small Biot number represents small resistance to heat conduction and thus small temperature gradient of body.But in Fig.11 temperature profile θ(y)and thermal boundary layer thickness increases with increase in Biot number Bi.
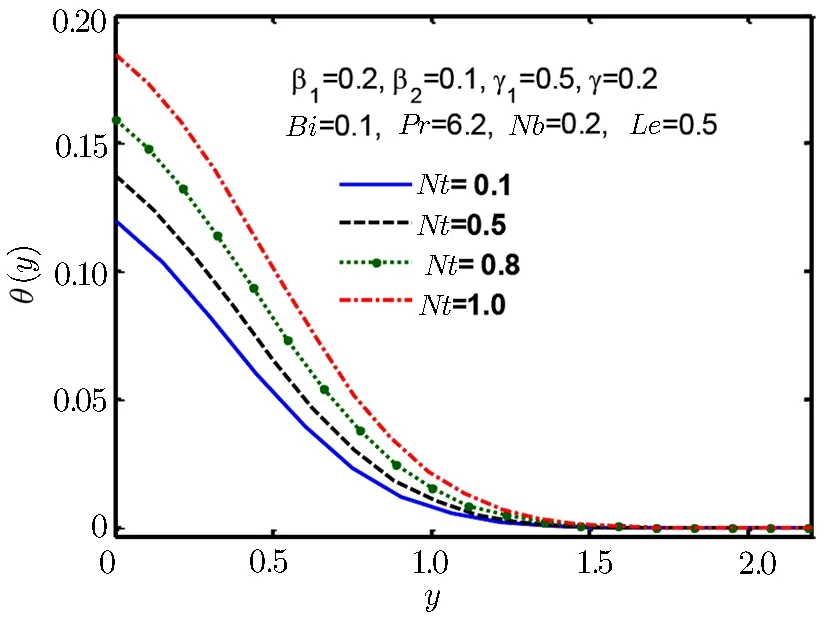
Fig.13 Temperature profile θ(y)for Nt.

Fig.14 Concentration profile ϕ(y)for β1.
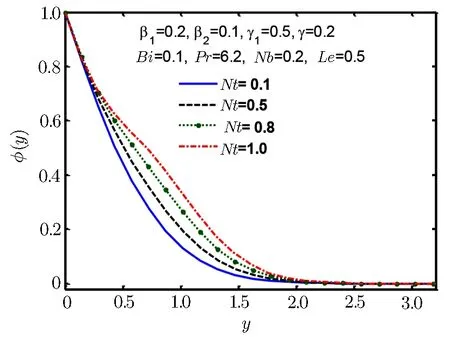
Fig.15 Concentration profile ϕ(y)for Nt.
Figure 12 shows increasing behaviour for thermophoresis parameter Nt and same type of behaviour is detected in Fig.13 for Brownian motion parameter Nb.Increasing thermopherotic and Brownian motion parameter Nt and Nb,increases of temperature in boundary layer which subsequently lessens heat transfer rate at surface.There would be a significant reduction in concentration boundary layer thickness when Lewis number Le is enlarged.This spectacle happens,since Lewis number affects the concentration gradient at the surface.
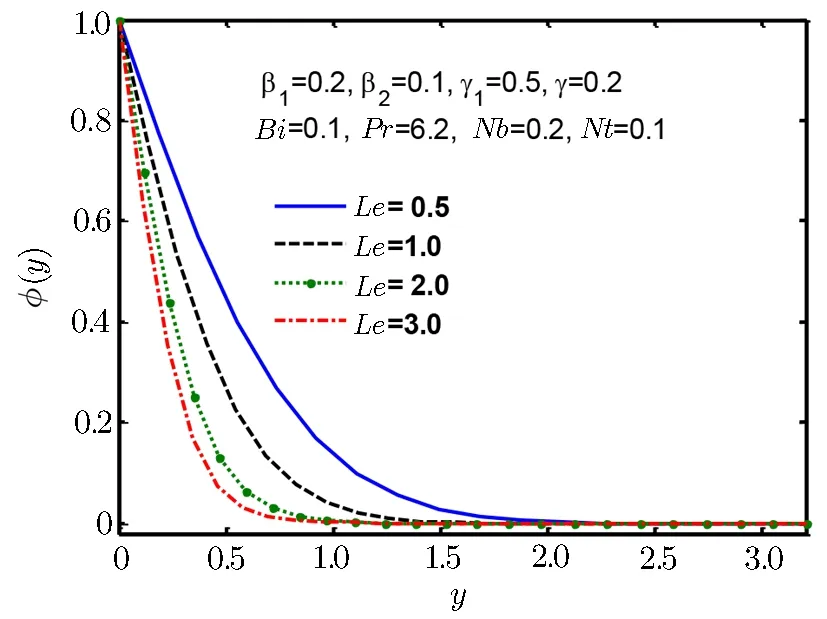
Fig.16 Concentration profile ϕ(y)for Le.
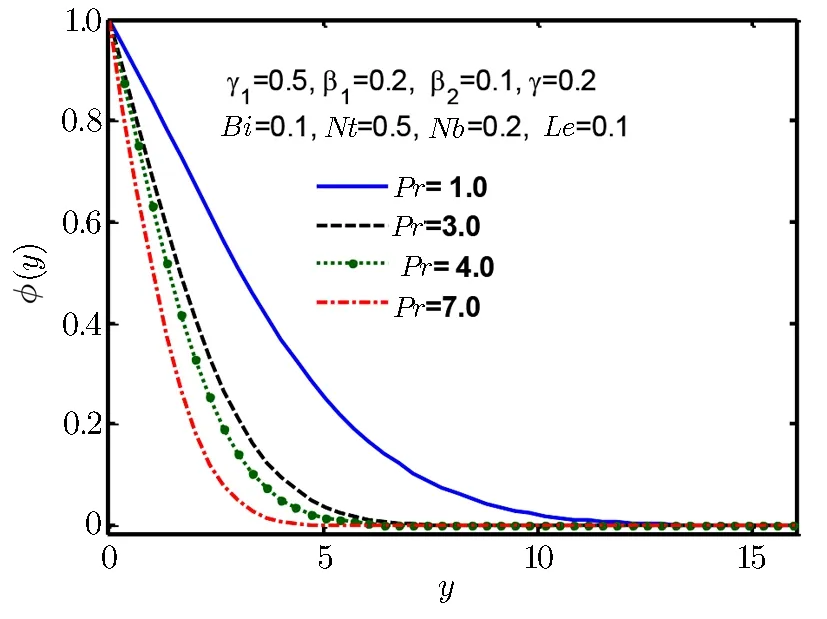
Fig.17 Concentration profile ϕ(y)for Pr.
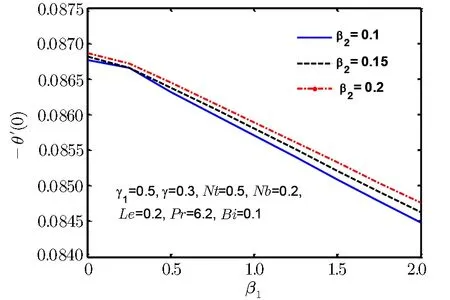
Fig.18 Surface heat flux −θ′(0)for β1.
Figures 14–17 are plotted to examine the nature of concentration profile ϕ(y).Figure 14 shows increasing effect for increase in Deborah number β1and Fig.15 shows increasing effect for increase in thermophoresis parameter Nt,but Fig.16 shows decreasing behaviour for increase in Lewis number Le and similar kind of behaviour is observed in Fig.17 for Prandtl number Pr.It is fascinating to note that molecular Brownian motion of nanoparticles at nano scale levels is a significant nano scale mechanism that governs their thermal behavior.

Fig.19 Surface mass flux −ϕ′(0)for β2.
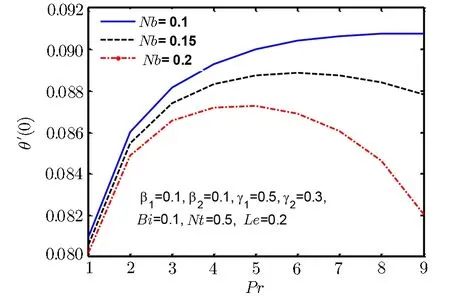
Fig.20 Surface heat flux −θ′(0)for Nb.
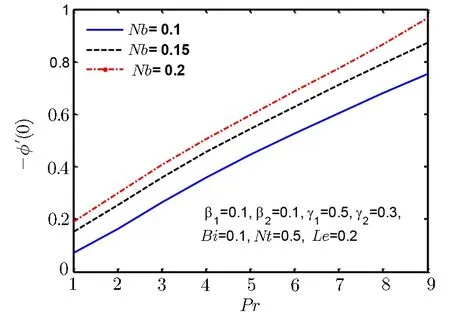
Fig.21 Surface mass flux −ϕ′(0)for Nb.
Since the size of the nanoparticles is very tiny so Brownian motion revenues that can affect heat transfer properties.Since the size of particle tactics to nano-meter gage,Brownian motion of relative particle and its effects on the adjacent fluids become vital in heat transfer.It is also detected that both temperature and volume fraction of the nanofluid within boundary layer increase by increasing in thermophertic parameter Nt and hence the nanoparticles enhance heat and mass transfer.Nanoparticle volume fraction distributions slow down by an increment in Lewis number in whole area.Lewis number is proportion of thermal diffusivity to mass diffusivity.Growing the values of Lewis number results a higher value of while smallest value of mass diffusivity,which results in thinner boundary layer.Figures 18–21 are plotted to examine the local heat flux and mass flux for different emerging parameter.It is observed that local heat flux −θ′(0)rises for Deborah number β2in Fig.18 and local mass flux −ϕ′(0)tends to increase for Deborah number β2in Fig.19.Further local heat flux −θ′(0)decreases as shown in Fig.20 while Fig.21 shows that local mass flux −ϕ′(0)tends to increase with Brownian motion parameter Nb.Since rising values of Prandtl number has a great heat volume,and hence strengthens the heat transfer rate.Figure 22(a)depicts stream line patterns for positive obliqueness when β1=0.Figure 22(b)exhibits streamline patterns for β1=0.Stream line shows that obliqueness constraint γ2creates change in direction of flow.We see that streamlines are inclined to left when obliqueness of flow is taken to be positive.Actually increase in γ2results in obliqueness of flow on a stretched area.Similarly Fig.23(a)exhibits streamline patterns for negative values of γ2when β1=0 while Fig.23(b)exhibits streamline patterns for negative values of γ2when β1=4.The stream contour ψ=0 touches the partition y1=0,at stagnation point x1=x0and zero skin friction.For conventional purpose we use y instead of y1in graphs.
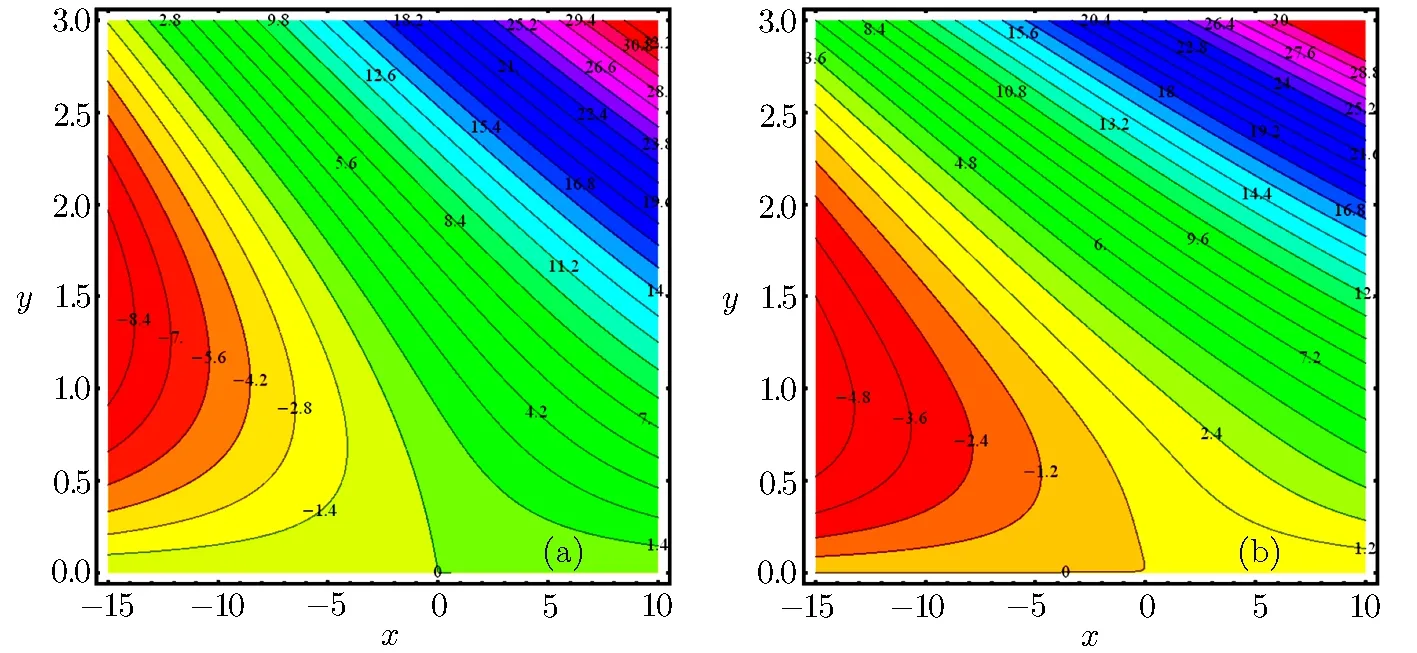
Fig.22 (a)Stream lines pattern for Deborah numbers β1=4,with γ2=5.(b)Stream lines pattern for Deborah numbers β1=0,with γ2=5.
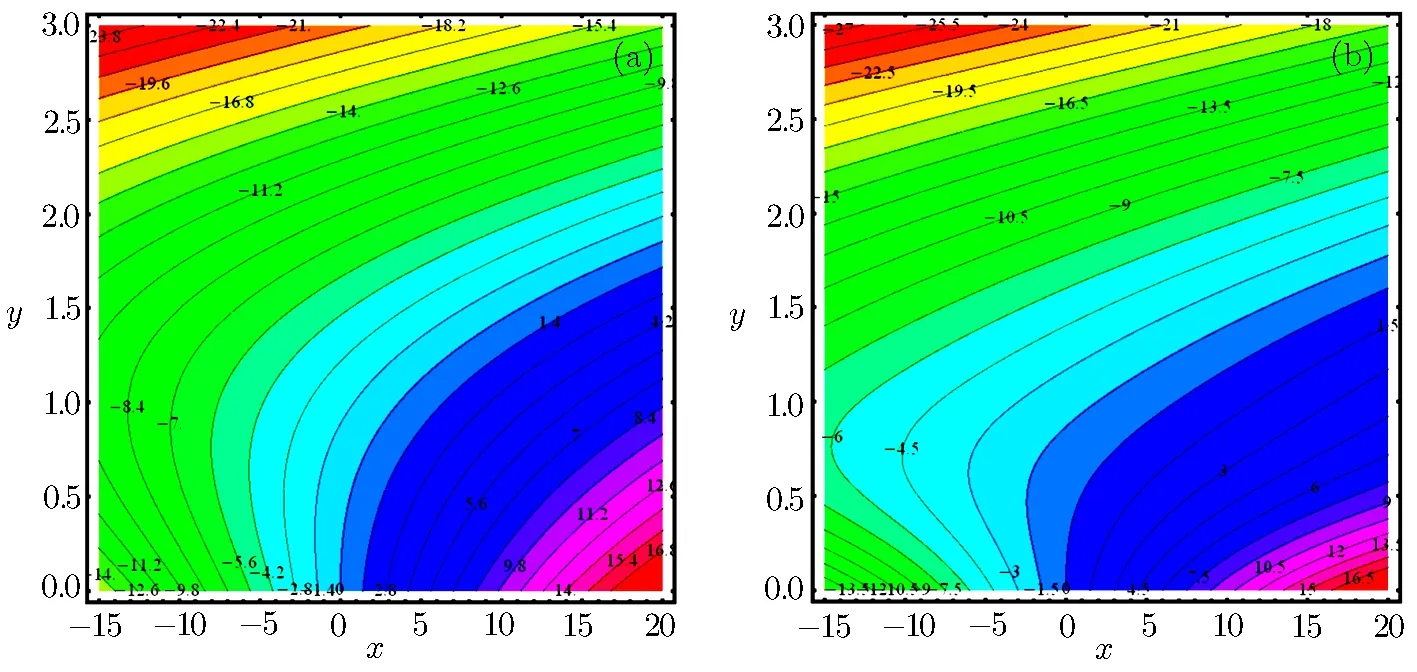
Fig.23 (a)Stream lines pattern for Deborah numbers β1=0,with γ2= −5.(b)Stream lines pattern for Deborah numbers β1=4,with γ2= −5.
6 Concluding Remarks
Oblique flow of an Oldroyd-B type fluid over a stretched surface had been explored with existence of internal heating and thermophoresis and Brownian motion properties.Main findings of this article are summarised as:
Deborah number β1becomes the reason for decrease in momentum boundary layer but it goes for increase in thermal boundary layer.Also,local heat and mass fluxes decrease for Deborah number β1.Brownian motion decreases the local heat flux while it enhances the local mass flux at the stretching surface.Streamlines patterns exhibit that the flow is more inclined in the presence of the Deborah number.
[1]S.Nadeem and A.Hussain,Zeitschrift für Naturforschung A 65(2010)540.
[2]R.Mehmood,S.Nadeem,and N.S.Akbar,J.Taiwan Inst.Chem.Eng.44(2013)586.
[3]S.Nadeem,R.Mehmood,and N.S.Akbar,J.Comput.Theor.Nanosci.10(2013)2737.
[4]S.Nadeem,R.Mehmood,and N.S.Akbar,Int.J.Heat Mass Transfer 57(2013)679.
[5]M.Rahman,T.Grosan,and I.Pop,Int.J.Numer.Method H.26(2016)189.
[6]L.Howarth,Lond.Edinb.Dubl.Phil.Mag.42(1951)239.
[7]T.Chiam,J.Phys.Soc.Jpn.63(1994)2443.
[8]Y.Lok,A.Ishak,and I.Pop,Int.J.Numer.Method H.21(2011)61.
[9]L.J.Crane,Z.Angew.Math.Phys.21(1970)645.
[10]R.Cortell,Int.J.Nonlinear Mech.41(2006)78.
[11]E.Pohlhausen,Z.Angew.Math.Phys.1(1921)115
[12]A.Aziz,Commun.Nonlinear Sci.Numer.Simul.14(2009)1064.
[13]E.Magyari,Commun.Nonlinear Sci.Numer.Simul.16(2011)599.
[14]A.Ishak,Appl.Math.Comput.217(2010)837.
[15]Z.Haddad,et al.,Int.J.Therm.Sci.57(2012)152.
[16]S.Nadeem,R.U.Haq,N.S.Akbar,et al.,PLoS ONE 8(2013)e69811.
[17]M.Sheikholeslami,et al.,Comput.Fluids 94(2014)147.
[18]M.Sheikholeslami,et al.,J.Magn.Magn.Mater.374(2015)36.
[19]G.Seth,M.Mishra,and A.Chamkha,J.Nano fluids 5(2016)511.
[20]P.Reddy and A.Chamkha,J.Appl.Fluid Mech.9(2016)2443.
[21]A.M.Rashad,B.Mallikarjuna,A.J.Chamkha,et al.,Afrika Matematika(2016)1.
[22]O.Makinde and A.Aziz,Int.J.Therm.Sci.49(2010)1813.
[23]A.V.Kuznetsov and D.Nield,Int.J.Therm.Sci.49(2010)243.
[24]G.Swapna,L.Kumar,P.Rana,and B.Singh,et al.,J.Taiwan Inst.Chem.Eng.47(2015)18.
[25]W.Ibrahim and O.Makinde,J.Aerospace Eng.29(2015)04015037.
[26]M.Rahman,A.V.Rosca,and I.Pop,Int.J.Numer.Method H.25(2015)299.
[27]A.Malvandi,F.Hedayati,and D.Ganji,J.Appl.Fluid Mech.8(2015).
[28]K.Das,P.R.Duari,and P.K.Kundu,J.Egyptian Math.Soc.23(2015)435.
[29]R.Kandasamy,C.Jeyabalan,and K.S.Prabhu,Appl.Nanosci.6(2016)287.
[30]V.Rajesh,Mallesh,and O.A.Bég,Procedia Mater.Sci.10(2015)80.
[31]A.Rashad,Ismael,A.Muneer,et al.,J.Taiwan Inst.Chem.Eng.68(2016)173.
[32]P.S.Reddy,P.Sreedevi,and A.J.Chamkha,Heat Transfer Asian Res.46(2016)815.
[33]A.U.Rehman,R.Mehmood,and S.Nadeem,Appl.Therm.Eng.112(2017)832.
[34]P.S.Reddy and A.J.Chamkha,Int.J.Numer.Method H.27(2017)1.
[35]P.S.Reddy,A.J.Chamkha,and A.Al-Mudhaf,Powder Technol.28(2017)1008.
[36]S.Rana,R.Mehmood,and N.S.Akbar,J.Mol.Liq.222(2016)1010.
[37]P.S.Reddy and A.J.Chamkha,J.Porous Media 20(2017)1.
[38]S.Rana,R.Mehmood,P.V.S.Narayana,and N.S.Akbar,Commun.Theor.Phys.66(2016)687.
[39]R.Mehmood,S.Nadeem,S.Saleem,and N.S.Akbar,J.Taiwan Inst.Chem.Eng.74(2017)49.
[40]R.Mehmood,S.Nadeem,and N.S.Akbar,J.Appl.Fluid Mech.9(2016)1359.
[41]S.Nadeem,R.Mehmood,and N.S.Akbar,J.Magn.Magn.Mater.378(2015)457.
 Communications in Theoretical Physics2018年7期
Communications in Theoretical Physics2018年7期
- Communications in Theoretical Physics的其它文章
- Upshot of Chemical Species and Nonlinear Thermal Radiation on Oldroyd-B Nano fluid Flow Past a Bi-directional Stretched Surface with Heat Generation/Absorption in a Porous Media∗
- Galerkin Finite Element Study on the Effects of Variable Thermal Conductivity and Variable Mass Diffusion Conductance on Heat and Mass Transfer∗
- The Three-Pion Decays of the a1(1260)∗
- A New Calculation of Rotational Bands in Alpha-Cluster Nuclei
- A Numerical Investigation of 3D MHD Rotating Flow with Binary Chemical Reaction,Activation Energy and Non-Fourier Heat Flux∗
- Detection of Magnetic Field Gradient and Single Spin Using Optically Levitated Nano-Particle in Vacuum∗
