复指数函数的定义及欧拉公式的教学探讨

高 杰 笪 诚 朱仁义

（巢湖学院，安徽 合肥 236148）

1 引言

欧拉公式在《复变函数与积分变换》[1]课程中具有十分重要的地位，在定义复指数函数后，应用欧拉公式直接给出对数函数、幂函数、三角函数以及反三角函数的定义，从而将初等函数从实数域扩展到复数域。但在给出复指数函数定义之前，并没有说明为什么f（z）=ex（cosy+isiny）就是复数域上的指数函数。与此同时，在欧拉公式：eiθcosθ+isinθ中，等式的左边是复指数函数，等式的右边是余弦函数和正弦函数；复指数函数怎么会和余弦函数与正弦函数之间存在关系？这是学生在学习过程中一定会有的疑惑，也是教师在教学过程中必须要说明的问题。

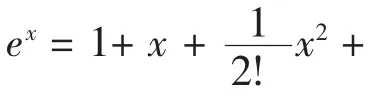
正因为在教学过程中，复指数函数的定义交代不够清楚，导致学生在理解上存在偏差，给复变函数后续章节以及其他课程的学习带来一定的障碍。

2 复指数函数定义

众所周知，在实数域中指数函数被定义为y=ax（其中a＞0且a≠1一切实数），当a取值为自然数e时，我们得到工程中常用的指数函数y=ex（本文中提到的指数函数，如不加说明均是以e为底），该指数函数满足以下几个条件：

i.定义域内是连续函数

ii.（ex）′=ex，e0=1

iii.ex满足指数律：

若能构造一个复函数 f（z） =u（x，y） +i（x，y），其中 z=x+iy 为复数，使其满足以下条件：

iv.f（z）在复平面上处处解析

v.f′（z）=f（z），f（0） =1

vi.f（z）满足指数律： f（z1+z2） =f（z1） f（z2）即

vii.当 Im（z）=0 时，f（z）=ex

那么这个函数f（z）就可以定义为是复变量z的指数函数，并把它记作：f（z）=ez，下面我们试图找到能够满足题设条件iv-vii的函数f（z）。

首先由条件 iv，假设定义在复平面上的解析函数 f（z） =u（x，y） +i（x，y）（其中 z=x+iy），则由解析函数的充要条件知：

由条件v和（1）式，可得以下微分方程组：

由方程中①和②不妨设方程组（2）的通解为：

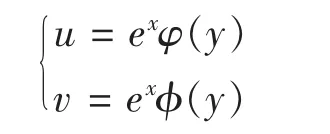
其中的φ（y）和φ（y）是关于y的实函数，代入③和④中，解得：

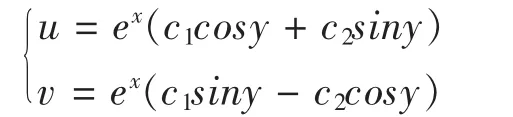
代入初始条件 f（0）=1，得：

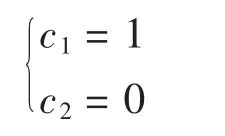
即有：

则满足条件iv和v的解析函数（1）的表达式应为：

下面验证（3）式是否满足条件vi和vii？

首先，设有两个复变数： z1＝ x1+iy1，z2＝ x2+iy2，则由（3）式可得：

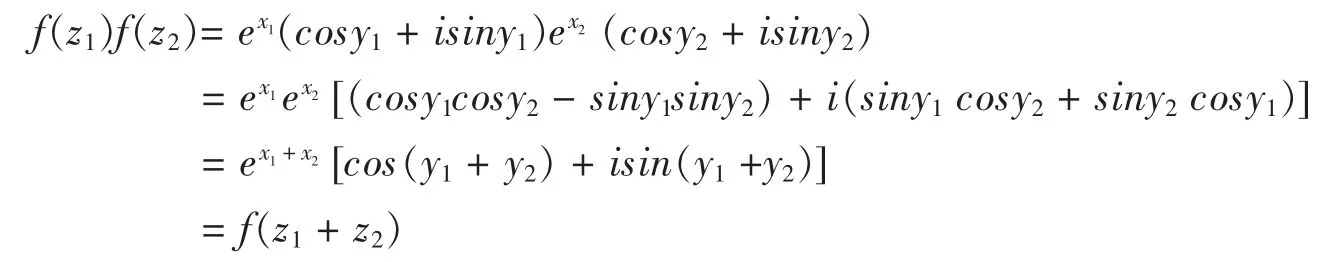
可知 f（z）满足条件 vi。

其次，当Im（z）=0即y=0，则（3）式退化为实数域的指数函数：

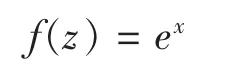
可知 f（z） =ex满足条件 vii。

因此，（3）式即可作为指数函数从实数域推广到复数域后的定义，记为：

需要指出两点：第一，定义式中第一个等式也可以写成exp（z），ez没有幂的意义，是一个数学符号，为了与实数域中的指数函数表达方式统一并简化表达式和运算，其中的e严格意义上并不代表实数域中的自然数；第二，复指数函数除了有iv—vii的性质外，同时也具备在实数域中没有的性质，比如：周期性，周期为2kπi（其中：k∈Z）。至此，在不引入复分析概念的情况下，从已知的实数域指数函数的定义和性质出发，给出复指数函数为何具有如此形式的定义式。

3 欧拉公式的可视化

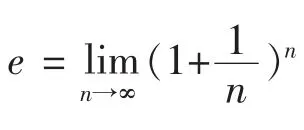
其中 z为任意的复数[7]。由（5）式，以纯虚数为例，分别考察 eπi和 e2πi，可得：

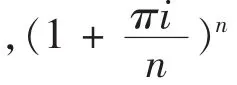
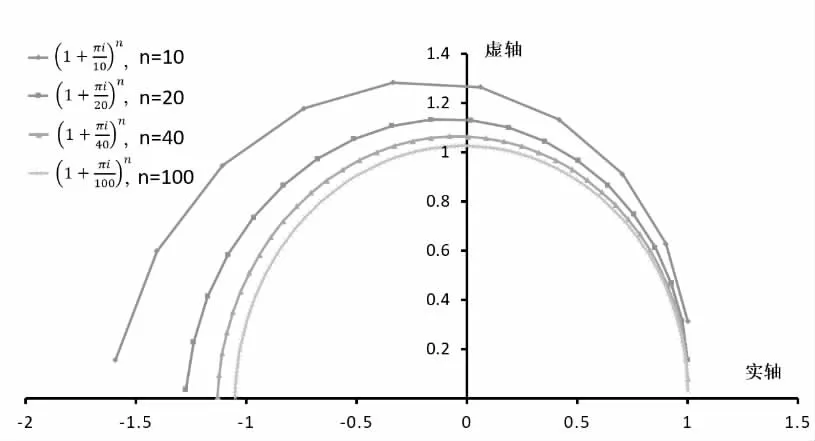
图1 eπi数值逼近过程

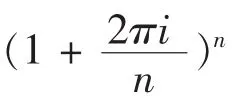
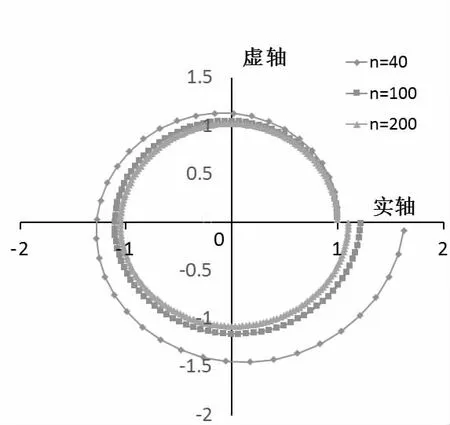
图2 e2πi逼近过程

由（5）式的逼近过程可知：eiθ可代表复平面单位圆周上的任意一点，θ即为该点与实轴正半轴的夹角。由表达式（4），若假设z为纯虚数iθ，则有：

表达式（6）即为欧拉公式。其图像如图3所示：

图3 欧拉公式的可视化描述

在复平面上，单位圆周上的任一点A，其位置可以用虚指数函数eiθ来表示，其中θ为A的辐角主值，可以看出与上述数值模拟的逼近过程一致。

进一步，推广到整个复平面，对于复平面上任意一点z=x+iy，可以表示为：

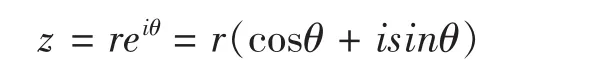
分别对应于复数的指数和三角形式，其中r为z的模，θ为z的辐角

至此，对于任意复指数函数f（z）＝az（其中a＞0且a≠ 1一切实数，z为一切复数），有：

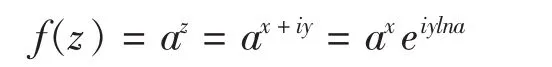
其对应复平面上模为ax，辐角主值为ylna的点。

4 教学探讨

由于教材中直接给出复指数函数定义式，进而引入欧拉公式，没有指出定义的来历，很大程度上影响学生对复变函数及欧拉公式的理解。鉴于以上情况，建议在教学过程中从以下几个方面加以展开：

4.1 还原知识发现的过程

欧拉通过严格的推导发现了eiθ=cosθ+isinθ的关系，要知道在欧拉的时代，还没有复数概念，这不能不说是欧拉的伟大所在。随着数的范围由实数扩展到复数后，特别是高斯等人将复数与复平面上的点对应起来，有关的复变函数理论才得以建立。在理论建立的过程中，人们自然要提出一个问题：实数域的初等函数，如：指数函数、对数函数、幂函数、三角函数等，推广到复数域后是什么？本着朴实、简单的数学思维，自然希望上述函数推广到复数域后，仍然有和实数域中类似甚至一样的运算性质。本文即按照这一思路，从运算性质入手，给出复指数函数应该被定义成何种表达式。

4.2 尊重知识的认知过程

学生开始接触复指数函数，对于复数的指数幂在理解上存在一些困难，特别是对于eiθ，受到实数域中指数函数定义的影响，首先想到的是这个指数幂的值是多少？此时，需要向学生们明确两点：首先，此处的eiθ之所以写成e的指数幂的形式，是为了与实数域的指数函数在表达式上统一，是一个记号，并没有幂的意义；其次，这也是正是欧拉公式的意义所在，通过欧拉公式建立了虚指数函数与三角函数之间的联系，让复指数的运算成为可能，并具有和实数域指数函数有近乎一样的运算性质。

4.3 注重新旧知识的融会贯通

引导学生回顾《高等数学》中的重要极限，由e的定义出发，通过数值模拟的方法，直观的给出eiθ在复平面上的图像；同时，也可以利用级数展开知识，分别将eiθ，cosθ，sinθ展开成泰勒级数形式，他们之间也是满足：eiθ=cosθ+isinθ。