不可压缩超弹性Rivlin类材料组成球形薄壳动力响应

赵 振 涛， 袁 学 刚＊，， 张 洪 武， 赵 巍， 张 文 正

（1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.大连民族大学 理学院，辽宁 大连 116600）

0 引 言

超弹性材料的典型代表有橡胶材料、类橡胶材料和生物软组织等.因其具有高弹性、大变形等特点，广泛应用于航空航天、机械工程、医疗器械等领域.从力学性能上讲，超弹性材料也称为Green弹性材料，其本构关系可由应变能函数给出，常见的有neo-Hookean材料、Mooney-Rivlin材料、Yeoh材料等.作为一种常见的材料模型，Rivlin类模型广泛应用于橡胶材料的模拟，如丁腈橡胶、天然橡胶、氯丁橡胶、硫化橡胶等；同时，Rivlin类模型形式简单，材料参数较少，使用该模型进行数值模拟可以得到很好的效果［1－2］.此外，由于与实验数据有较好吻合程度，有限元分析中也常使用Rivlin类模型对橡胶制件进行分析，如轨道用橡胶扣件受力和寿命分析［3］.

关于超弹性材料及其结构的动力响应问题的研究源于Knowles［4］的工作，他利用材料的不可压缩条件和结构的对称性研究了无限长不可压缩弹性圆柱管轴对称振动问题，并将问题约化为一维非线性问题，给出了超弹性材料模型振动问题的一般形式解，从而奠定了此类问题的研究基础.随着有限变形理论和非线性动力学理论的发展，越来越多的学者致力于超弹性结构动力学问题的研究.相关问题的研究进展可参见Aranda-Iglesias等［5］和 Alijani 等［6］的 综 述.其 中，Calderer［7］研究了球壳和柱壳结构在突加荷载下的动力学问题，给出了荷载对解的定性性质的影响.Yuan等［8－9］研究了周期阶梯荷载下不可压缩超弹性材料组成的球膜和圆柱壳的动力学问题，给出了周期振动的条件.为了分析超弹性本构关系对球形薄膜动态膨胀的影响，Rodríguez-Martínez等［10］采用6种不同形式的应变能函数分析了不同的常值荷载和加速度下球壳的变形和振动问题，指出了对于同样的变形，不同的材料模型会改变系统的稳定性.Aranda-Iglesias等［11］对超弹性圆柱壳结构的径向振动进行了研究，分别对修正的Mooney-Rivlin模型和具有不变量高阶项的Yeoh模型进行分析和比较，并指出，Yeoh模型提供了比Mooney-Rivlin模型更保守的预测性.为了更加深入了解橡胶材料的性能，并对其行为进行准确模拟，Treloar［12］和 Kawabata等［13］使用硫化橡胶进行了各种变形实验，然后通过实验数据拟合得到Rivlin类模型的材料参数，并进行了相应的变形分析.

本文的目的是在已有研究工作的基础上，运用有限变形理论和非线性动力学理论，研究不可压缩超弹性Rivlin类材料组成的球形薄壳的动力响应问题，并进行必要的定性分析.

1 球形薄壳的运动模型

对于由不可压缩超弹性材料组成的球形薄壳，当薄壳的内表面受突加常值荷载作用时，考察薄壳的径向对称运动.在球坐标系中，薄壳的初始构型表示为

其中R1和R2分别表示薄壳的内外半径.在球对称变形假设下，变形后构型表示为

其中r（R，t）是径向变形待定函数.用于描述两种构型映射关系的变形梯度张量F＝diag｛r／R，r／R，r／R｝，其中λ1＝r／R，λ2＝λ3＝r／R，分别表示薄壳的径向和环向主伸长.

根据材料的不可压缩条件λ1λ2λ3＝1，即，对其两端关于R积分，可以得到

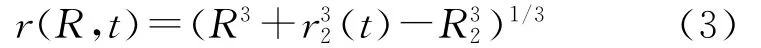
其中r2（t）＝r（R2，t），是一个只与时间t相关的待求函数.易见，式（3）可以完全描述薄壳随时间演化的径向运动.

对于不可压缩超弹性材料组成的薄壳，Cauchy应力的主分量为

其中p（r，t）是静水压力，W＝W（λ1，λ2，λ3）是不可压缩超弹性材料的应变能函数.

忽略体积力的作用时，描述薄壳径向对称运动的平衡微分方程为

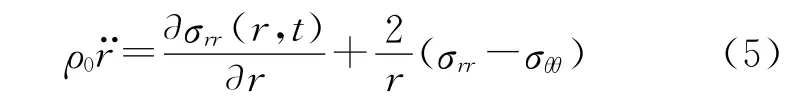
其中ρ0表示材料密度，表示r（R，t）关于时间t的二阶导数.

在初始时刻，薄壳未发生变形且处于静止状态，于是相应的初始条件为

薄壳的内表面受到与时间无关的径向均布常值荷载p（p＞0）的作用，且外表面无约束时，应力的边界条件可以表示为

本文中，考虑多项式形式的Rivlin类不可压缩超弹性材料模型，其应变能函数的一般形式为［14］

式中：Am、Bn为材料参数；I1、I2是右 Cauchy－Green张量C的两个主不变量，它们与主伸长λ1、λ2、λ3有如下关系：

特别地，当式（8）中的参数Am、Bn取一些特殊值时，该模型可以退化为常见的neo-Hookean、Mooney-Rivlin和Yeoh等形式的材料模型.

2 模型求解

2.1 控制方程量纲一化

对式（3）关于时间t求二阶导数，并进行整理得到

将式（4）和（10）代入式（5），然后对得到的方程关于r积分，由边界条件（7）得到1

其中r1（t）＝r（R1，t）.

为了便于定性分析，引入如下量纲一变换：

其中δ表示薄壳的厚度参数，x表示薄壳外表面的变形.

将应变能函数形式（8）重新记为

其中am1＝Am1／A1，bn1＝Bn1／A1.

于是，式（11）可约化为如下形式的量纲一方程：

其中

此外，初始条件（6）变为

2.2 首次积分解

将式（14）两边同时乘以x2x.，然后关于时间t积分，根据初始条件（18），得到如下首次积分解：

其中

是势能函数.

令x.＝y，式（14）转化为如下的一阶微分方程组：

易见，方程的平衡点为（xe，0），其中xe满足方程H（x；δ）－＝0，换句话说，对于给定的荷载，可以根据该方程确定平衡点的个数.

当薄壳的结构参数给定时，系统的动力响应主要受材料的本构关系及突加荷载的影响.通过对曲线的渐近线和系统平衡点个数的讨论，进而可以对系统的动力响应进行定性分析.

3 方程定性分析

3.1 平衡点的个数

当参数m、n取不同值时，表1、2分别给出了薄壳变形曲线的渐近线和平衡点个数的变化情况.

表1 变形曲线的渐近线随应变能函数中m、n的变化Tab.1 The change of asymptotic curves of deformation curves for different m，n in strain energy functions

表2 平衡点的个数Tab.2 The number of equilibrium points

表1中，水平渐近线和斜渐近线表示变形曲线在x→＋∞时的渐近线类型；“－”表示相应的变形曲线不存在水平或斜渐近线.

由表1、2不难看出，当m＝1，n＝0时，系统最多有2个平衡点，对应的变形曲线有递增和递减两个分支并且有水平渐近线；当m＝1，2且n＝0，1时变形曲线存在渐近线，其他情况不再有渐近线.不难得出如下结论：当m、n继续增大时，系统的行为不再发生定性的变化.

3.2 球形薄壳的动力响应

薄壳的厚度取为δ＝0.01，初始条件为（1，0）.下面利用非线性动力学理论中的相平面分析法，结合数值算例对超弹性薄壳结构的动力响应问题进行定性分析，主要涉及周期振动、振幅跳跃以及结构破坏等.

特别地，当薄壳做周期运动时，由于薄壳在最大振幅xmax处满足xx＝xmax＝0，对于给定的荷载，根据式（19）求得xmax，进而描述薄壳振动的周期为

3.2.1 m＝1，n＝0应变能模型响应 当m＝1，n＝0时，式（8）退化为neo-Hookean应变能模型.此时，该模型只含有I1－3的线性项.图1给出了变形曲线以及不同荷载时的势能曲线、相轨迹和时程曲线.

图1 系统的变形曲线、势能曲线、相轨迹和时程曲线（m＝1，n＝0）Fig.1 The deformation curves，potential energy curves，phase diagrams and time history curves of the system （m ＝1，n＝0）

图2给出了周期运动时系统周期和振幅随荷载变化的关系.由图2可见，对于每一个小于临界值的荷载，都对应着确定的周期和振幅，并且它们随荷载的增大而增大.但是当时，系统运动不再有周期性，薄壳的变形会随时间一直变大，直到破裂.

图2 周期和振幅曲线（m＝1，n＝0）Fig.2 The period and amplitude curves（m＝1，n＝0）

3.2.2 m＝1，n＝1应变能模型响应 当m＝1，n＝1时，式（8）退化为 Mooney-Rivlin应变能模型.此时，该模型存在材料参数b11.由表1可见，变形曲线始终存在斜渐近线，所以系统至少存在一个平衡点.如图3中的曲线，材料参数影响系统平衡点的个数，并存在临界材料参数b11cr＝0.214.

（1）b11＝0.1

此时，b11＜b11cr.图3给出了不同材料参数的变形曲线及不同荷载时的势能曲线、相轨迹和时程曲线.

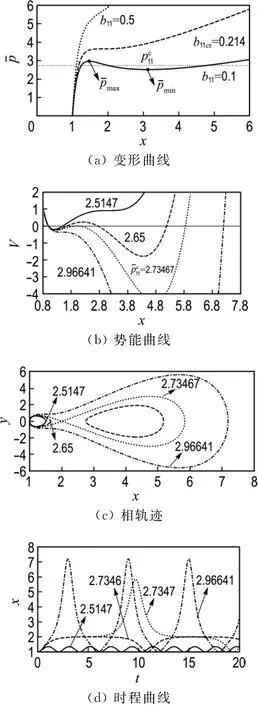
图3 系统的变形曲线、势能曲线、相轨迹和时程曲线（m＝1，n＝1）Fig.3 The deformation curves，potential energy curves，phase diagrams and time history curves of the system （m ＝1，n＝1）

图4给出了系统的周期和振幅随荷载变化的关系.由图可见，存在临界荷载＝2.734 67.当时，周期和振幅随荷载的增大而增大，并且在临界荷载处存在极限周期和振幅.当时，周期随荷载的增大而减小，振幅随荷载的增大而增大；当时，发生周期和振幅跳跃现象.

图4 周期和振幅曲线（m＝1，n＝1，b11＝0.1）Fig.4 The period and amplitude curves（m＝1，n＝1，b11＝0.1）

（2）b11＝0.25

此时，b11＞b11cr，图5给出周期运动时系统周期和振幅随时间变化的关系.

由图5可见，随着荷载的增大，系统做非线性周期振动，周期和振幅随荷载连续变化，虽然没有跳跃或者突变现象，但是周期曲线存在一个最大值，振幅曲线存在一个拐点.

3.2.3 其他情况 前面已经对m＝1，n＝0和m＝1，n＝1两种典型的应变能模型的响应问题进行了分析，这两种模型包含了表1中所有的渐近线类型和表2中所有可能的平衡点个数，图6给出了m、n取其他值时的情况.

由图6可见，材料参数对变形曲线的渐近线以及系统平衡点个数的影响与前两种典型情况相似，并且同样存在着临界材料参数.通过以上的分析验证可以知道，应变能函数中的参数m、n继续增大时，系统的动力响应并未发生定性的改变，只是在定量方面有一定的影响.

图5 周期和振幅曲线（m＝1，n＝1，b11＝0.25）Fig.5 The period and amplitude curves（m＝1，n＝1，b11＝0.25）

（2）荷载的大小影响系统振动的稳定性.如图1所示，存在临界荷载，相轨迹出现了非对称的“∝”型同宿轨道，当荷载超过临界荷载时，相轨迹不再封闭，即球形薄壳随时间的径向运动将无限增大，最终破裂；如图3所示，球形薄壳随时间的径向运动始终是一类非线性周期振动，但出现了非对称“∞”型同宿轨道，即存在临界荷载，当荷载超过临界荷载时，球形薄壳发生周期跳跃和振幅跳跃的现象，参见图4.

（3）对于Rivlin类材料模型，应变能函数中的低阶项能够定性描述结构的动力响应，增加高阶项能够更加准确地对其进行定量分析，但是不会出现新的响应类型.

图6 材料参数对平衡点个数的影响Fig.6 The effect of material parameters on the number of equilibrium points

4 结 论

（1）材料参数的取值影响系统平衡点的个数.如图6所示，存在临界材料参数，当材料参数小于临界参数时变形曲线有3个平衡点，当材料参数大于临界参数时变形曲线只有1个平衡点；在有些情况下，变形曲线有两个平衡点或不存在平衡点.