若干Mycielski图邻点可区别Ⅰ-均匀全染色
张 婷*1, 朱 恩 强, 赵 双 柱, 杜 佳
(1.兰州文理学院 师范学院,甘肃 兰州 730000;2.北京大学 信息科学技术学院,北京 100871;3.兰州文理学院 数字媒体学院,甘肃 兰州 730000)
0 引 言
关于均匀染色的概念最早是由Meyer[1]提出的,1994年,Fu[2]提出了均匀全染色概念以及均匀全染色猜想.许多学者围绕图的均匀全染色做了大量研究[3-5].文献[6-8]研究了一些特殊图的点可区别Ⅰ-全染色和邻点可区别Ⅰ-全染色.文献[9]给出了路、圈、扇、轮、完全图、完全二部图的邻点可区别Ⅰ-均匀全色数,提出邻点可区别Ⅰ-均匀全色数最大不超过2的猜想;文献[10]研究了几类图的均匀邻点可区别Ⅰ-全染色.本文根据图M(Pn)、M(Cn)和 M(Sn)的构造特征,利用函数构造法,研究并确立它们邻点可区别Ⅰ-均匀全色数,并验证其满足猜想.
1 相关定义和引理
定义1[11]对于阶数不小于2的连通图G(V,E),设f是从V(G)∪E(G)到{1,2,…,k}的映射,k为自然数,如果f满足
(1)对uv∈E(G),u≠v,有f(u)≠f(v);
(2)对 uv,uw∈E(G),v≠w,f(uv)≠f(uw);
(3)对uv∈E(G),u≠v,C(u)≠C(v)则称f为图G的一个邻点可区别的Ⅰ-全染色(简记为k-Ⅰ-AVDTC).记χiat(G)=min{k|G 的k-Ⅰ-AVDTC}为图G的邻点可区别Ⅰ-全色数.其中C(u)={f(u)}∪{f(uv)|uv∈E(G)}称为点u在f下的色集,C(u)在色全集合C={1,2,…,k}中的补集记为C(v)=C\C(u).
定义2[9]设f 是简单连通图G(V,E)(V(G)≥2)的一个k-Ⅰ-AVDTC,若满足i,j∈{1,2,…,k},i≠j,有 Ti-Tj≤1,则称f为图G的一个k-邻点可区别Ⅰ-均匀全染色(简记为k-Ⅰ-AVDETC),而称(G)=min{k|G 的k-Ⅰ-AVDETC}为图G的邻点可区别Ⅰ-均匀全色数,其中 Ti=Vi∪Ei,Vi={v|v∈V(G),f(v)=i},Ei={e|e∈E(G),f(e)=i}.
定义 3[12]对简单图 G,若V(M(G))=V(G)∪V′∪{w},E(M(G))=E(G)∪{uv′|u∈V(G),v′∈V′,uv∈E(G)}∪{wv′|v′∈V′},其中V′={v′|v∈V(G)},{w}∩(V∪V′)=,称图M(G)是图G的Mycielski图.
猜想1[9]对简单连通图G,有(G)≤Δ(G)+2.
引理1[9](G)≥Δ(G),Δ(G)表示图G的最大度.
引理2[9]对 V(G)≥2的连通图G,若有最大度点相邻.
文中未加说明的符号或术语可参见文献[13].
2 主要结论
定理1 设Pn表示阶为n(n≥3)的路,则有
证明 以下分3种情形证明本定理.
情形1 当n=3时,Δ(M(P3))=4,由引理1知(G)≥Δ(G),为证定理为真,只需给出M(P3)的一个4-Ⅰ-AVDETC.为此,构造映射f:V(M(P3))∪E(M(P3))→{1,2,3,4},f(v1)=f(v′1)=f(v1v2)=f(v3v′2)=1;f(v2)=f(v′2)=f(v2v′1)=f(v′3w)=2; f(v3)=f(v′3)=f(v2v′3)=f(v′2w)=3;f(v2v3)=f(v1v′2)=f(v′1w)=f(w)=4.
为验证上述全染色法f是邻点可区别的,现列出各顶点的色集合:
C(v1)={1,4};C(v2)=C(v′2)=;
C(v3)={1,3,4};C(v′1)={1,2,4};
C(v′3)={2,3};C(w)={2,3,4}
可见f是M(P3)的一个4-Ⅰ-AVDTC,并且显然有 Ti=4,i=1,2,3,4.
由定义知f是M(P3)的一个4-Ⅰ-AVDETC.
情形2 当n=4时,由于M(P4)有两个相邻的最大度点,且Δ(M(P4))=4.由引理2知,(M (P))≥Δ(M (P))+1=5,为 证44(M(P))=5,只需给出 M(P)的一个5Ⅰ44--AVDETC.为 此 构 造 映 射 f:V (M (P4))∪E(M(P4))→{1,2,3,4,5},f(vi)=f(v′i)=i,i=1,2,3,4;f(vivi+1)=i,i=1,2,3;f(v′iw)=i-1,i=2,3,4;f(v1v′2)=f(v3v′4)=f(v4v′3)=f(w)=5;f(v2v′3)=f(v3v′2)=f(v′1w)=4;f(v2v′1)=3.
此时需验证
C(v1)={1,5};C(v2)={5};C(v3)={1};
C(v4)={3,4,5};C(v′1)={1,3,4};
C(v′2)={3};C(v′3)={1};
C(v′4)={3,4,5};C(w)=
从而f是M(P4)的一个5-Ⅰ-AVDTC,且有
由定义知f是 M(P4)的一个5-Ⅰ-AVDETC.
情形3 当n≥5时,M(Pn)只有一个最大度点w,由引理1知,χiaet(G)≥Δ(G)=n.为证定理为真,只需给出 M(Pn)的一个n-Ⅰ-AVDETC,为此构造映射f:V(M(Pn))∪E(M(Pn))→{0,1,2,…,n-1},f(vi)=f(v′i)=f(vivi+1)=(i+1)mod n,i=1,2,…,n-1;f(vn)=1;f(v′n)=0;f(w)=1;f(viv′i+1)=(i+2)mod n,i=1,2,…,n-1;f(viv′i-1)=(i+3)mod n,i=2,3,…,n;f(v′w)=imod n,i=1,2,…,n.
此时需检验
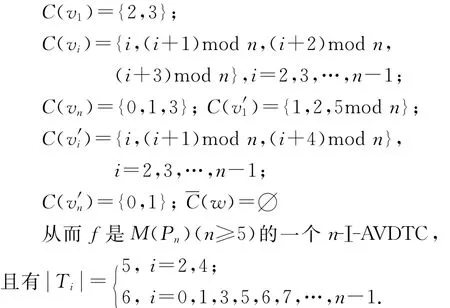
由定义知f 是M(Pn)(n≥5)的一个n-Ⅰ-AVDETC.
综合以上情形,定理得证.
定理2 设Cn表示阶为n(n≥3)的圈,则有
证明 以下分3种情形证明本定理.
情形1 当n=3时,M(C3)有相邻的最大度点,且Δ(M(C3))=4,由引理2有χiaet(M(C3))≥Δ(M(C3))+1=5.为证χiaet(M(C3))=5,只需给出M(C3)的一个5-Ⅰ-AVDETC.为此构造映射f:V(M(C3))∪E(M(C3))→{1,2,3,4,5},f(v1)=f(v1v′2)=f(v2v′1)=f(w)=1;f(v2v′3)=f(v3v′2)=f(v′1)=2;f(v1v′3)=f(v2v3)=f(v′2)=f(v′1w)=3;f(v3v1)=f(v2)=f(v′3)=f(v′2w)=4;f(v3)=f(v1v2)=f(v3v′1)=f(v′3w)=5.
此时需要检验
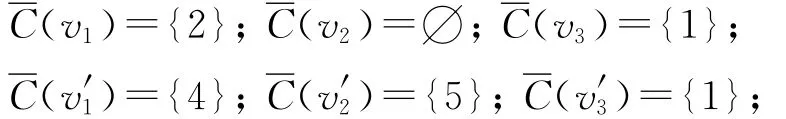
C(w)={2}
从而f是M(C3)的一个5-Ⅰ-AVDTC,且有
由定义知f是M(C3)的一个5-Ⅰ-AVDETC.
情形2 当n=4时,M(C4)有相邻的最大度点,且Δ(M(C4))=4,由引理2知,(M(C4))≥Δ(M(C4))+1=5.为证(M(C4))=5,只需给出M(C4)的一个5-Ⅰ-AVDETC.为此构造映射f:V(M(C4))∪E(M(C4))→{1,2,3,4,5},f(vi)=i,i=1,2,3,4;f(v′i)=5,i=1,3,4;f(v′2)=2;f(w)=4;f(vivi+1)=i,i=1,3;f(v2v3)=f(v4v5)=5;f(v1v′2)=f(v2v′1)=3;f(v2v′3)=f(v3v′2)=4;f(v3v′4)=f(v4v′3)=1;f(v4v′1)=f(v1v′4)=2;f(v′iw)=i,i=1,2,3,4.
此时需检验
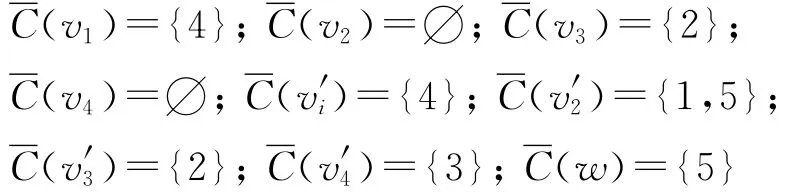
从而f是M(C4)的一个5-Ⅰ-AVDTC,且有Ti=5,i=1,2,3,4,5.
由定义知f是M(C4)的一个5-Ⅰ-AVDETC.
情形3 当n≥5时,M(Cn)只有一个最大度点w,由引理1知,χiaet(M(Cn))≥Δ(M(Cn))=n,为证定理为真,只需给出 M(Cn)的一个n-Ⅰ-AVDETC.由 于 V (M (Cn))=V (M (Pn)),E(M(Cn))=E(M (Pn))∪ {vnv1}∪ {v1v′n}∪{vnv′1}.
故若可能,可思考在定理1情形3的基础上对 M(Pn)再添加3条边vnv1、v1v′n、vnv′1,并对其着以适当的颜色,得到 M(Cn)的一个n-Ⅰ-AVDETC即可.为此,在定理1情形3的基础上,令f(vnv1)=1,f(v1v′n)=4,f(vnv′1)=2.再检验C(v1)={1,2,3,4},C(vn)={0,1,2,3},C(v′1)={1,2,5mod n},C(v′n)={0,1,4}.而其他所有点的色集合未变,显然,对任意的uv∈E(M(Cn)),有C(u)≠C(v).
从而f为M(Cn)的一个n-Ⅰ-AVDTC.又由
由定义知f是M(Cn)的一个n-Ⅰ-AVDETC.
综合以上情形,定理得证.
定理3 设Sn表示阶为n+1(n≥3)的星,则有
证明 由图 M(Sn)的结构知Δ(M(Sn))=2n,由 引 理 1 知 χiaet(M (Sn))≥2n.为 证χi(M(S))=2n,只需给出 M(S)的一个2nⅠ
aetnn--AVDETC.为 此 构 造 映 射 f:V (M (Sn))∪E(M(Sn))→{1,2,…,2n},f(vi)=f(v′i)=i+1,i=0,1,2,…,n;f(w)=2n;f(v0vi)=i,i=1,2,…,n;f(v0v′i)=f(v′0vi)=n+i,i=1,2,…,n;f(v′iw)=i+1,i=0,1,2;f(v′iw)=n+i-1,i=3,4,…,n.
此时需检验
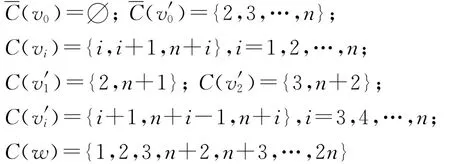
从而f 是 M (Sn)(n≥3)的一个 2n-Ⅰ-
由定义知f是M(Sn)(n≥3)的一个2n-Ⅰ-AVDETC,可以看出猜想1对上述定理中的图是成立的.
3 结 语
图的邻点可区别Ⅰ-均匀全染色是一个较新的概念,目前对于图的邻点可区别Ⅰ-均匀全色数的研究甚少,本文利用函数构造法,研究并确立了图M(Pn)、M(Cn)和 M(Sn)的邻点可区别Ⅰ-均匀全色数,验证了邻点可区别Ⅰ-均匀全色数对于这些特殊图成立,具有一定的理论意义和实际意义.

