高考一类问题的深度挖掘
安徽省芜湖市十二中学 (241002)
金 奎
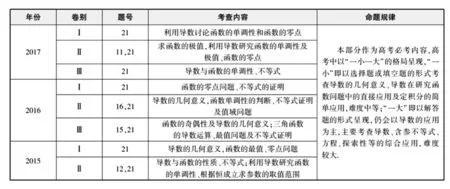
导数在函数中的应用是高考中考查的重点同时也是难点,下面总结近三年高考导数考查内容和命题规律如下表
全国新课标高考中常常把运用导数来解决函数的零点问题,下面我们讨论运用导数来证明零点问题,这类问题往往需要构造对称函数来解决.运用导数解决零点问题旨在考查考生利用导数工具分析解决与函数有关的问题,解决这类问题非常困难,往往需要打破常规思路,运用所学的知识寻找合理的解题思路,巧妙构造关于直线x=a对称的函数来解决求值和证明问题.下面我们从2016年全国新课标Ⅰ的导数题入手,进行问题探讨分析,进行深度挖掘.
一、真题呈现,思路探析
例1 (2016年全国新课标Ⅰ)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点x1,x2,证明:x1+x2<2.
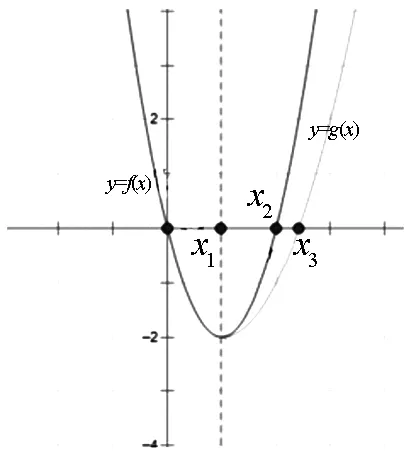
图1
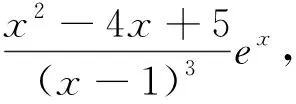
构造函数g(x)=f(2-x)=-xex+a(x-1)2,再令F(x)=f(x)-f(2-x)=(2x-2)ex(x>1),易知当x>1时,F(x)>0,不妨设x2>1>x1,若f(x2)=g(x3)=f(2-x1)=0,则x2 归纳总结:从上述导数问题的求解可以发现采用将问题转化为两个分问题进行研究,首先通过导数研究原函数的图像,得到关于x=1的对称函数,从而构造新的函数,使问题更为直接、简单.下面我们将此类题型进行合理变形,深度挖掘. 例2 (2018年山东济南市高三一模)已知函数f(x)=ax-lnx(a∈R). (1)求函数f(x)的单调区间; 归纳总结:上述的证明问题,我们通过巧妙的变形,深度挖掘,将问题转化为例1的零点证明问题,首先通过导数研究原函数的图像,得到关于x=a的对称函数,从而构造新的函数,使问题更为直接、简单.当然本题还可以用更加简单的方法进行证明. 例3 (2018年安徽省芜湖市高三一模)已知函数f(x)=lnx-x-m(m<-2). (2)设x1,x2是函数f(x)的两个零点,且x1 (2)x1x2<1⟺lnx1+lnx2<0(令t=lnx)⟺t1+t2<0,令函数g(t)=-et+t-m有两个零点为t1,t2,∵g′(t)=-et+1,易知函数g(t)在(-∞,0)为单增函数,在(0,+∞)为单减函数, 令h(t)=g(-t),则F(t)=h(t)-g(t)= -e-t+et-2t(t>0),F′(t)=et+e-t-2≥0,∴F(t)在(0,+∞)为单增函数,故F(t)≥F(0)=0,当g(t2)=h(t3),t2 运用导数解决函数的零点是高考中的重要考点,求解时的巧妙变形,分析问题,将问题进行转化,深度挖掘,并归纳总结成具体化的一类问题;在教学过程中采用探究的分析方式来转化问题并不是无目的、无意识的,它是建立在学生充分掌握知识点、全面认识问题的基础之上,这就要求学生在平时的学习备考中从基础入手,围绕教材,巩固知识,深度挖掘,建立体系,有效提升学生的数学核心素养.二、试题衔接,探究再析
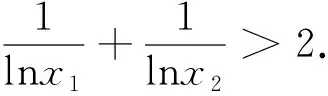
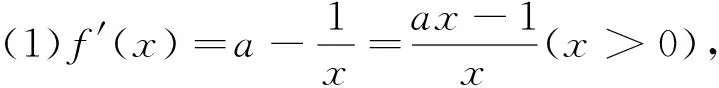
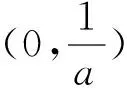

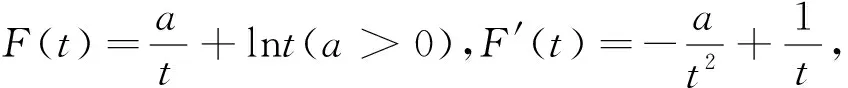
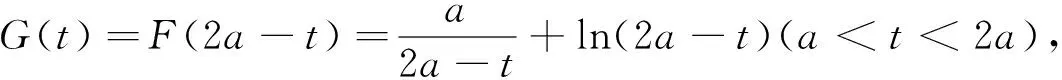
三、归纳总结,深度挖掘