黏弹－Perzyna黏塑性有限元法应力更新隐式算法

闫富有， 崔 昊， 张晓婉， 刘忠玉

（郑州大学 土木工程学院，郑州450001）

1 引 言

一些岩土或混凝土等材料，具有显著的流变性，可采用黏弹－黏塑性模型来描述其应力应变关系［1］。黏弹性部分通常由基本黏弹性元件串联或并联的不同组合来描述，黏塑性部分可采用简单的Bingham模型或更具一般性的Perzyna等模型［1，2］来描述与应变率相关的塑性流动。在计算过程中，允许应力点偏离屈服面，在应力更新过程中无需让应力点返回屈服面［2，3］。对于应力点必须返回屈服面，即满足屈服函数等于0的条件，称之为黏弹－塑性模型［4］，以便区别于本文的黏弹－黏塑性模型。无论是否屈服、加载或卸载，其变形特性均表现为与时间相关的高度非线性，且与应变历史相关。数值计算模型通常比较庞大，计算时间长，其计算效率、精度和收敛性以及解的稳定性在很大程度上取决于应力更新算法［2－4］。

显式积分算法是目前普遍应用的黏弹－黏塑性本构积分算法［5－8］。计算简单，但未考虑黏弹性应变历史，需要严格的更小的时间步长限制，应力漂移现象值得商榷［3，4］。为了弥补显示算法的不足，文献［4，9，10］基于黏弹性松弛模量Prony级数的表达式导出应力递推公式，然后与塑性［4］或黏塑性耦合［9，10］，后者仅限于简单的 Mises屈服函数和黏塑性流动模型。对于常用的由Kelvin链与弹簧或黏壶串联而成的黏弹性模型，其松弛模量并非显式，复杂模型松弛模量的推演也较难，导致计算程序很难通用化。基于蠕变柔度导出应力－应变递推公式的方法源于文献［11］，后在文献［12，13］得到应用。该方法避免了松弛模量方法的不足，但把Mises屈服应力导入递推公式［11］，并假定与应力相关的一些变量在一个时步内为常数，不便应用于其他黏塑性问题。有限元法应力更新算法包括应力的更新和一致切向矩阵的计算，一些文献仅给出初步的应力递推算法［12，13］，而无具体计算公式，更没有表述与算法对应的一致切向矩阵［5，12，13］。研究多采用 Bingham 黏塑性模型［5－13］，而更具一般性的Perzyna模型［3］很少应用于岩土工程中。一些商业有限元软件只能进行黏弹性或弹－黏塑性分析［14］，尚不能进行黏弹－黏塑性耦合计算，限制了其应用。

本文针对黏弹性和双曲型Drucker－Prager屈服函数［15］、各向同性硬化及 Perzyna黏塑性［2，3］耦合模型，给出完全隐式的应力更新算法和最终公式。首先，基于黏弹性蠕变柔度，通过定义与弹性问题相对应的与时间增量相关的黏弹性剪切模量和体积模量，实现遗传积分方程的线性化，然后与黏塑性耦合。为了保证计算过程的稳定性，把Perzyna黏塑性定律转化为与弹塑性问题相对应的一致性条件，建立了黏塑性增量因子在大于0的条件下，由小于其收敛值的一侧逐步逼近其收敛值的单侧逼近算法。最后，通过ABAQUS软件提供的UMAT材料子程序完成计算，并对其收敛性进行讨论。

本文中1表示二阶单位张量，（1）ij＝δij，I和Is均为四阶张量，（I）ijkl＝δikδjl，（Is）ijkl＝（δikδjl＋δilδjk）／2，δij为 Kronecker delta，i，j，k，l＝1，2，3。∶表示两个张量的双点积，表示张量积，张量s的模定义为s＝

2 本构方程

2．1 黏弹性

对于图1所示的黏弹－黏塑性模型，其黏弹性部分是由一个弹簧、一个黏壶和多个Kelvin体串联而成。若仅有一个Kelvin体相串联，则为常规的Burgers体；若无黏壶η0，则为标准线性黏弹性体。ηvp为黏塑性黏性系数。把应变率张量ε·分解为黏弹应变率和黏塑性应变率［3，4］

式中 上标ve和vp分别代表对应参量的黏弹和黏塑性部分，变量上部的·为相对于时间的变化率。

黏弹性偏应变张量eve和体积应变εvev所对应的黏弹性蠕变柔度Jg和Jk分别为［11，12］

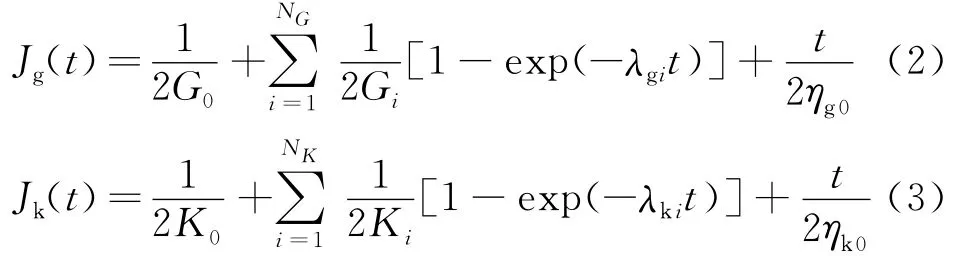
式中t为时间，下标g和k分别为与剪应力和平均应力所对应的量。λgi＝ηgi／Gi，λki＝ηki／Ki。Gi和Ki，ηgi和ηki，ηg0和ηk0分别为与图1的Gi，ηi和η0相对应的模型参数。NG和NK分别为剪应力和平均应力所对应的黏弹性模型中串联的Kelvin体个数，i＝1，2，…，NG／NK。

偏应变和体积应变分别由遗传积分方程给出

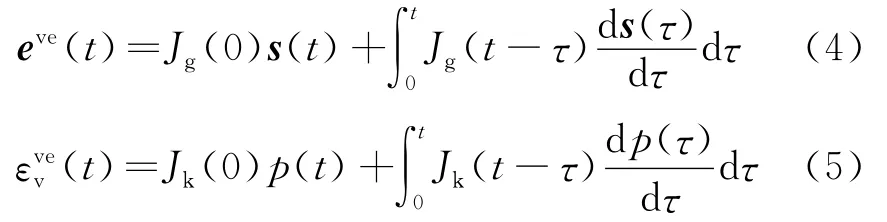
式中s和p分别为偏应力张量和平均应力，Jg（0）和Jk（0）分别为t＝0时所对应的量。

2．2 黏塑性

双曲线Drucker－Prager塑性屈服函数为［14］

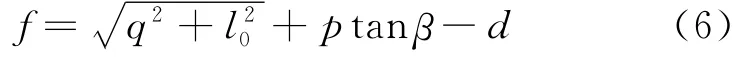
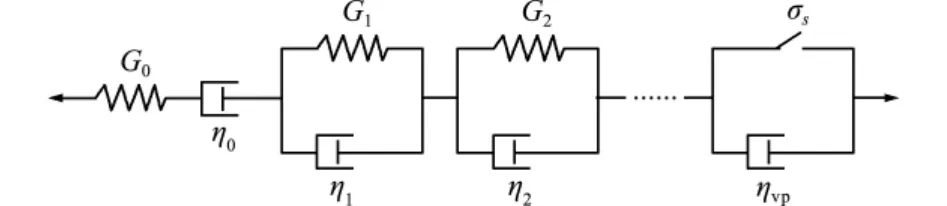
图1 黏弹－黏塑性模型Fig．1 A viscoelastic－viscoplastic model

式中β为与内摩擦角相关的参量，可由 Mohr－Coulomb与Drucker－Prager模型参数的转换关系用内摩擦角计算得到。q＝，l0可由d的初值d0等参数计算，d为与硬化相关的参量。

双曲型Drucker－Prager塑性模型虽然增加了计算过程的复杂性，但保证了屈服函数的连续性，使得在屈服面锥顶塑性流动方向具有唯一性，消除了线性Drucker－Prager屈服面锥顶的应力不连续性所导致的在其附近应力收敛的困难［15］，提高了计算效率和精度。两者的接近程度与参数l0的大小有关，当l0＜0．01时，运用线性和双曲线屈服函数所得的结果相当接近［15］。

把屈服函数和势函数写成一般形式，分别为

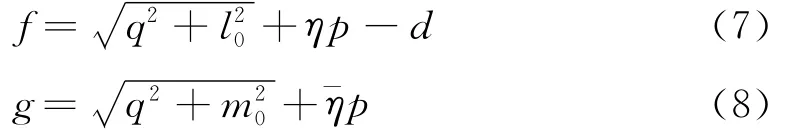
式中η＝tanβ，η－为将内摩擦角换为剪胀角Ψ后计算得到的η值。l0和m0均取一较小的正数，以便更好地接近于线性屈服函数。

仅考虑各向同性硬化，d为等效黏塑性应变ε－vp的函数，dd／dε－vp＝H，H 为硬化模量。对于线性硬化，H为常数，d＝d0＋Hε－vp。等效黏塑性应变率ε－·vp定义为［20］

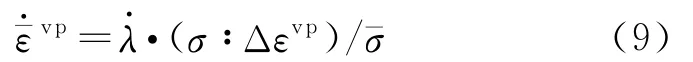
式中 Δεvp为Δt时间段的黏塑性应变增量，λ·为黏塑性增量因子，σ－为等效应力，本文取为单轴抗压强度sc。

黏塑性应变率由流动法则给出［3］

式中g，σ为势函数关于应力σ的偏导数。

采用Perzyna黏塑性模型［2，3］，黏塑性增量因子定义为

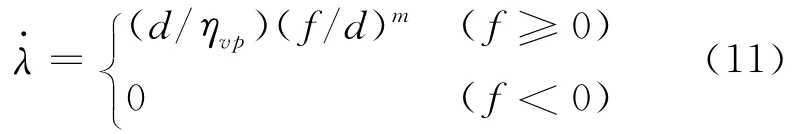
式中 模型参数m为黏塑性敏感性指数。当m＝1时，即为Bingham黏塑性模型。

3 本构积分算法

3．1 黏弹性

把式（2）代入式（4），整理后得

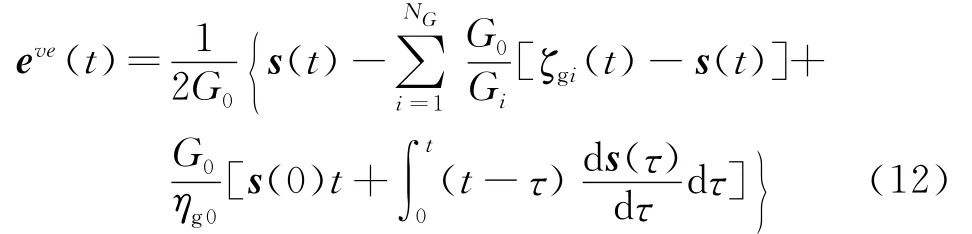
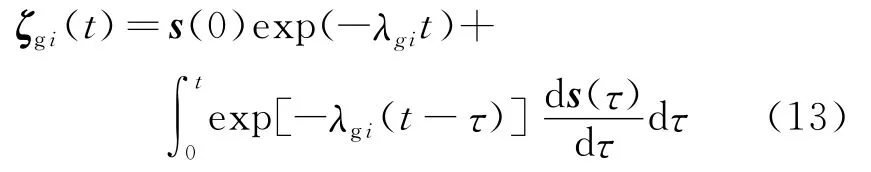
把时间t离散，下标n（n＝0，1，2，…）表示不同时步。t0＝0。第n＋1时步的时间增量记为Δtn＋1＝tn＋1－tn，偏应力增量记为 Δsn＋1＝sn＋1－sn，其他参量类同。在Δtn＋1时步内，假设应力线性变化，即ds（τ）／dτ为常数。对式（13）进行分段积分后，得tn＋1时刻ζgi（tn＋1）的递推公式为

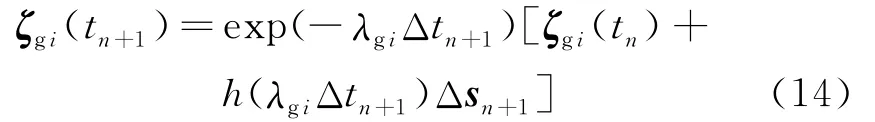
式中 h（x）＝［exp（x）－1］／x（变量x＝λgiΔtn＋1）。

把式（14）代入式（12），分别取t＝tn＋1和t＝tn，然后两式相减，并考虑最后一项的积分，得

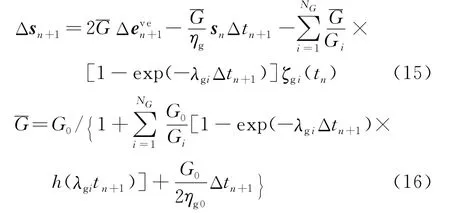
式（16）为考虑黏弹性应变历史和在每个时间步长内逐段线性化后用增量形式表示的黏弹性本构关系。对于平均应力p和黏弹性体积应变εvve，可根据相应的黏弹性模型，采用上述类似方法，得到n＋1时刻平均应力的表达式和与弹性问题相对应的黏弹性体积模量为

式中 状态变量ζki的表达式与式（13，14）相似，仅把其中的s和λgi分别换为p和λki即可。

由式（15，17）可知，下一时刻的应力增量由本时步黏弹性应变增量的影响项和考虑应变历史后状态变量ζgi及ζki的影响项两部分组成。

3．2 黏塑性

在计算过程中，黏塑性增量因子需满足式（11），即当屈服函数f＞0时，产生黏塑性应变。对时间差分后得

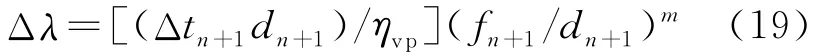
一般情况下，m＞1。如果f／d较小或较大，在计算过程中，式（19）往往不稳定［3，16］。把式（19）改写为与一般塑性问题类似的一致性条件为

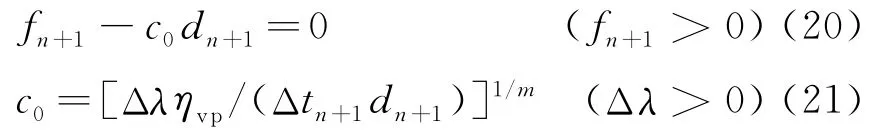
对于等效黏塑性应变，由式（9）得

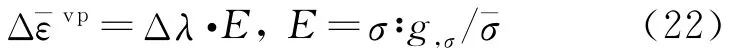
屈服函数和塑性势函数对σ的偏导数分别为

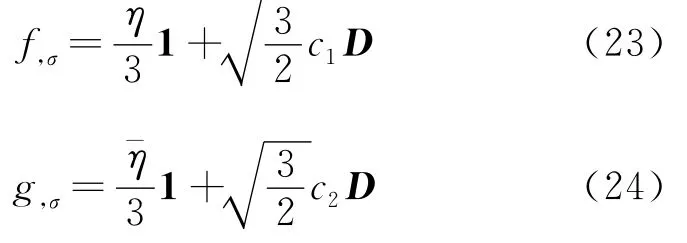
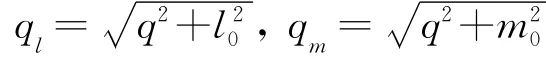
3．3 隐式应力更新算法

在3．1节中，定义了与时间增量相关的与弹性问题相对应的黏弹性剪切模量和体积模量，其增量形式的本构关系在形式上与弹性问题类似，可参考弹－黏塑性本构积分算法［3］进行应力更新。

在第n步计算结束后，对于新的时间段 ［tn，tn＋1］，给定总应变增量Δεn＋1，采用预估－校正两步法进行计算［3，4，11～13］。首先，把应变增量 Δεn＋1作为黏弹性试应变增量 Δεnve＋，t1ri，即Δεnve＋，1tri＝Δεn＋1。求得试应力增量Δσntri＋1及试应力σntri＋1。用试应力求得屈服函数f，若f≤0，该试应力即为实际应力，本时步计算结束；否则，进行黏塑性校正。

把试应变和实际应变增量代入式（15，17）后，并考虑式（10，23，24），得到实际应力和试应力的关系分别为

式中qntri＋1为由试应力求得的qn＋1，qm省略了表示时间的下标n＋1。

把式（25，26）一起代入黏塑性一致性条件式（20），并考虑c2为未知量，建立如下方程组，

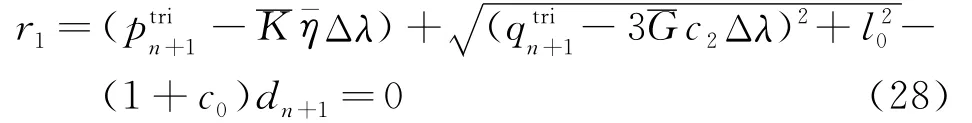
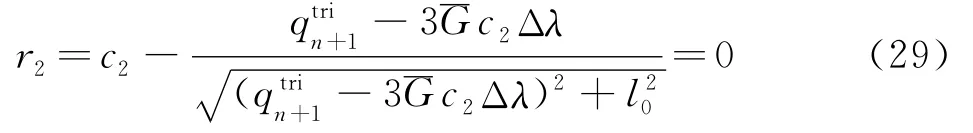
把式（28，29）改写为 N－R迭代格式

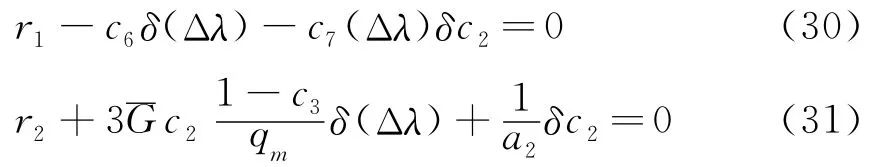
式中

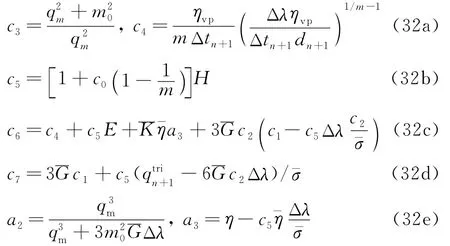
求解方程组（30，31）后得到δ（Δλ），更新Δλ，直到r1和r2小于规定的误差限（取10－8）后结束迭代。用收敛后的Δλ，应用式（25，26）即可求得平均应力和偏应力，黏塑性校正过程结束。然后，计算状态变量ζgi，ζki和ε－vp的值，以便下一时刻黏弹性计算。

3．4 一致切向矩阵

对于黏弹性状态，其一致切向矩阵Dve可仿照弹性问题给出［3，4］

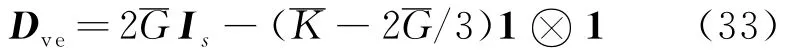
对于黏塑性状态，由一致性条件得

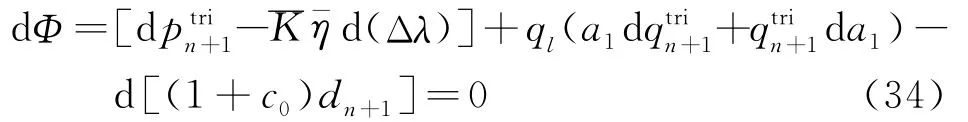
根据式（27）求得

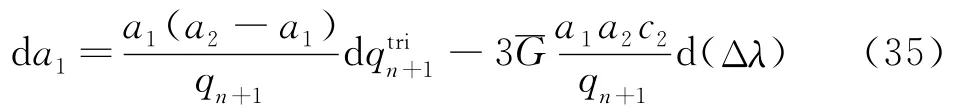
把式（35）代入式（34），经过冗长计算后得

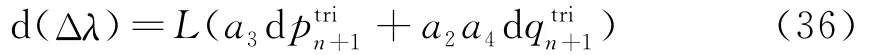
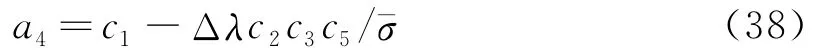
由式（25，26）对平均应力和偏应力微分，并考虑式（35，36）后，得黏弹－黏塑性一致切向矩阵Dvevp的表达式为

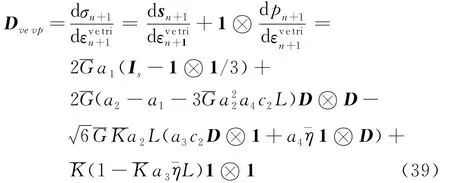
需要说明的是，在一致切向矩阵的公式中，采用了四阶张量Is，而不是四阶单位张量I，是因为有限元软件中采用的是工程应变。两者在张量运算过程中无差别，其差别仅体现在最后的计算上［3，4］。

4 算例分析和讨论

为了说明上述算法的有效性，采用ABAQUS提供的UMAT子程序［14］编制黏弹－黏塑性应力更新用户子程序，然后对有限元法计算结果进行分析和讨论。

4．1 算例分析

一地基模型，沿深度z、宽度x和另一方向y分别取10m，20m和1m。沿y方向划分为等厚度的4个单元，并对该方向的两侧施加零位移约束，以模拟平面应变问题［3，4］。在地基表面中间部位沿x方向作用一宽度为1m且随时间线性增加的条形荷载，荷载在180d内由0增大到500kPa，此后保持恒定。考虑对称性，在x方向取其一半进行计算。模型四周边界施加水平位移约束，模型底面约束三个方向的位移。分析采用三维有限元法，共划分2075个结点和1520个8结点六面体单元。

黏弹性部分的应力偏量和平均应力均采用一个弹簧、一个黏壶和两个Kelvin体串联而成，为扩展的Burgers模型（较常规的Burgers模型多为一个串联的Kelvin体），NG＝NK＝2。因试验参数有限，黏弹性参数由一维流变试验结果拟合得到，分别为 E0＝7．3MPa，η0＝15．6MPa·d，E1＝671．3MPa，η1＝25．3MPa·d，E2＝1246．8MPa，η2＝23570．8MPa·d。取泊松比为0．32，相对应的黏弹性参数分别为［4，9］

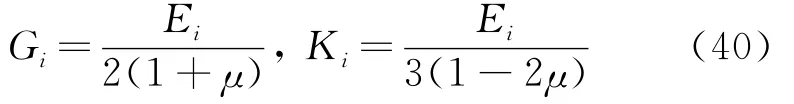
初始黏聚力c＝35kPa，内摩擦角φ＝15°，单轴抗压强度按σc＝2ccosφ／（1．0－sinφ）计算。采用与Mohr－Coulomb屈服面外切园近似的原则确定Drucker－Prager屈服面参数，即tanβ＝6sinφ／（3－sin φ），d的初值，l0和 m0均为0．001。按线性硬化考虑，硬化模量H＝37，选用关联流动法则，Ψ＝φ。有效重度取为9．0kN／m3。黏塑性黏性系数ηvp＝150MPa·d。

地应力平衡后，施加面力荷载。计算的时间步长Δt≈4d。为了验证本算法的有效性，取相同的黏弹性参数，将黏塑性敏感系数取不同值时，本文的计算结果与ABAQUS中的黏弹性计算结果［14］及文献［4］的黏弹－塑性计算结果进行比较。

分别取敏感性指数m＝1，5，10和20进行计算。地基表面荷载中心点处竖向位移和竖向应变εz随时间变化的结果比较分别如图2和图3所示。可以看出，在加载过程初期，由于尚未屈服，不同模型的计算结果基本相同；土体屈服后，不同模型的计算结果差别很大。黏弹性模型土体竖向位移和应变最小，黏弹－塑性模型的结果最大，黏弹－黏塑性模型的土体位移介于黏弹性和黏弹－塑性模型的计算结果之间。不同的黏塑性敏感性指数m对位移影响较大。当m＝1时（Bingham模型），其黏弹－黏塑性模型的位移最大；随着m的增大，变形相对减小。这与文献［3，16］的结论一致。当m＝20时，黏弹－黏塑性模型的竖向位移和应变几乎接近于黏弹性模型的结果。加载结束后，在恒定的荷载作用下，土体的蠕变行为持续增加，随着作用时间的延续，采用Bingham黏塑性模型计算的位移将逐步趋于黏弹－塑性的结果。因此，在实际工程中，可采用不同的敏感性指数试算，通过与实际结果比较拟合来确定一个合适的m值。

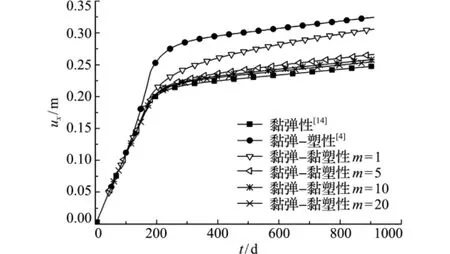
图2 荷载中心处竖向位移随时间变化结果比较Fig．2 Comparison of vertical displacement at the midpoint of loading

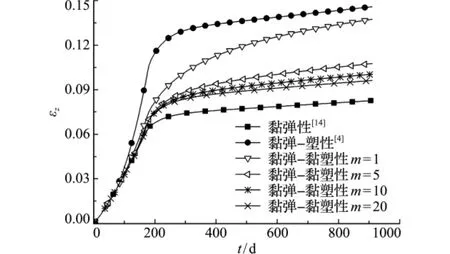
图3 荷载中心处竖向应变随时间变化结果比较Fig．3 Comparison of vertical strain component at the midpoint of loading

竖向平面内等效塑性应变云图如图4所示。由于等效黏塑性应变是根据应力和黏塑性应变定义的，在荷载对称面内呈现较大的值，塑性区的深度是有限的，其形状与弹－黏塑性［2］或黏弹－塑性［4］计算结果相似。

4．2 讨 论

时间步长的大小是影响计算精度的一个重要因素［3，4，15，16］。上述算例的时间跨度为910d，时间步长Δt≈4d，加载过程中每时步的荷载增量约为11．11kPa。表1给出了普通个人电脑上本文算法、文献［4］的黏弹－塑性算法和 ABAQUS黏弹性［14］计算的CPU时间比较。可以看出，本文的黏弹－黏塑性计算较ABQUS黏弹性计算约慢14%，尽管采用了隐式时间差分算法，其计算效率仍较高。

为了考察时间步长对计算结果的影响，取Δt≈2d，所用CPU时间几乎是Δt≈4d的2倍，两者的竖向位移之差绝对值的最大值小于1．8×10－3m，一些时间点的相对误差曲线如图5所示。可以看出，在荷载施加到最大值及其附近时，两者差别最大。随着蠕变的增加，误差很小，并没有因为时间步长增大一倍而产生计算结果的漂移。本文采用了完全隐式向后Euler算法，是可以采用较大时间步长而不出现应力漂移的一个重要原因。

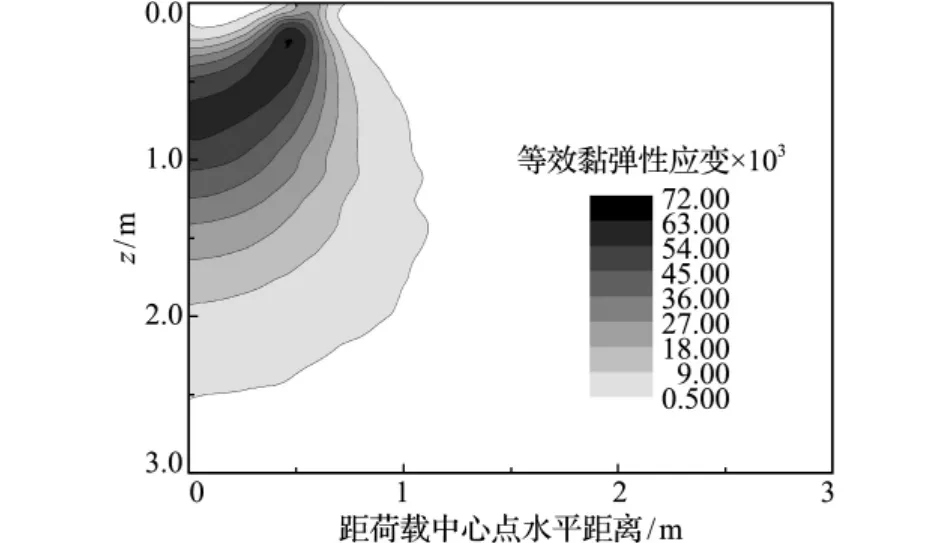
图4 土中累计等效黏塑性应变云图Fig．4 Contours of equivalent viscoplastic strain in soil

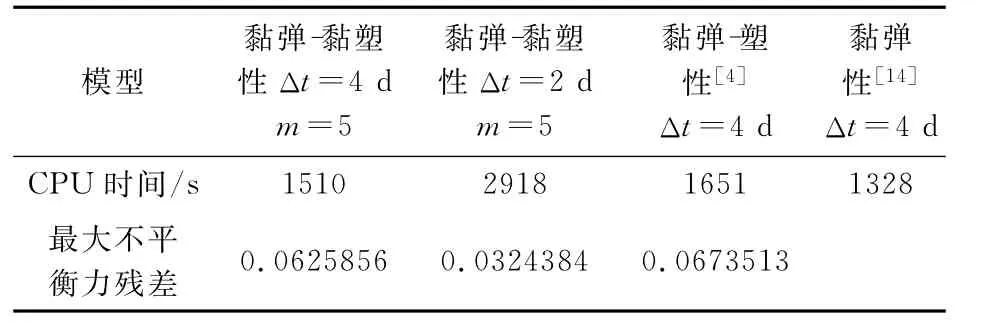
表1 有限元模拟CPU时间比较Tab．1 Comparison of CPU time for FEM simulations

分析迭代过程的收敛性。在每个迭代步，均需满足Δλ＞0和fn＋1＞0两个条件，否则，c0和c4就无法计算。在初始屈服或应力点距离屈服面很近时，由于Δλ的值往往很小（如10－20量级），Δλ的初始值不能取为0，且需要在Δλ＞0的一侧进行逼近，否则迭代不收敛。该问题是黏塑性隐式算法是否收敛的关键，也是不同于一般弹－塑性隐式算法之处［2，3，16］。文献［16］认为，Δλ取较好的初值才能保证收敛性。由于应力点偏离屈服面的程度不同，该初值往往很难选取。计算表明，如果Δλ的初值取为显式算法的计算值，应力点偏离屈服面较大时迭代基本都能收敛，但应力点在屈服面附近时往往不收敛。

解决该问题的关键是让Δλ在小于其收敛值的一侧逐渐逼近于其收敛值，且Δλ不能等于0。一方面，Δλ的初值取一个很小但不为0的值，如本文取Δλ＝10－30；另一方面，指定一个较该初值更小的正数，若迭代过程中Δλ小于该正数，参数c0和c4采用上一步的值而不再更新，避免出现双侧逼近收敛值的情况。反复计算表明，上述处理方法可以保证最终收敛。图6分别给出了取两个不同屈服函数值f时，黏塑性因子的迭代收敛情况。图6（a）收敛前后的屈服函数值差别很小，图6（b）收敛后f＝49．8787，均满足一致性条件。可以看出，无论应力点靠近屈服面还是偏离屈服面较大，经过十多次迭代运算，均能获得很好的收敛效果。由于已导出其解析式，计算效率和精度均比较高。

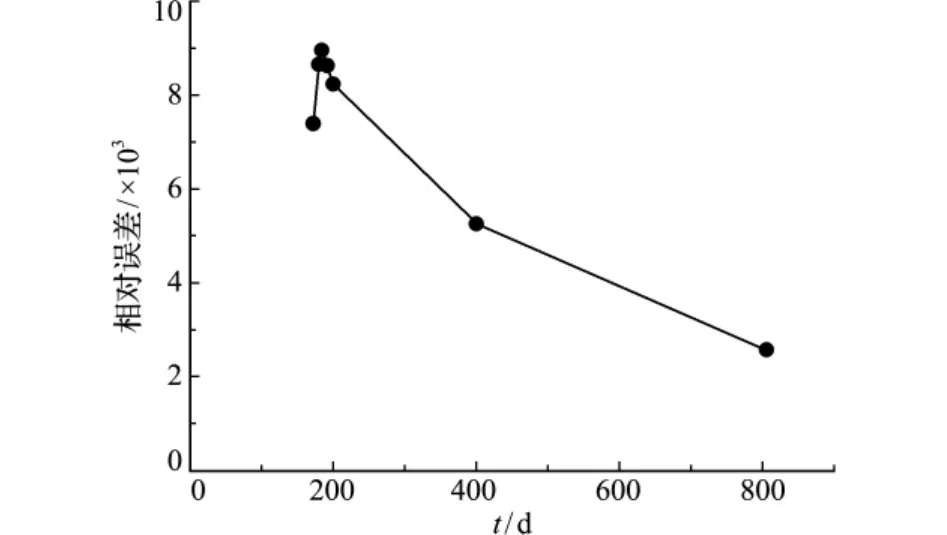
图5 时间步长Δt＝4d与Δt＝2d的相对误差Fig．5 Relative error betweenΔt＝4dandΔt＝2d

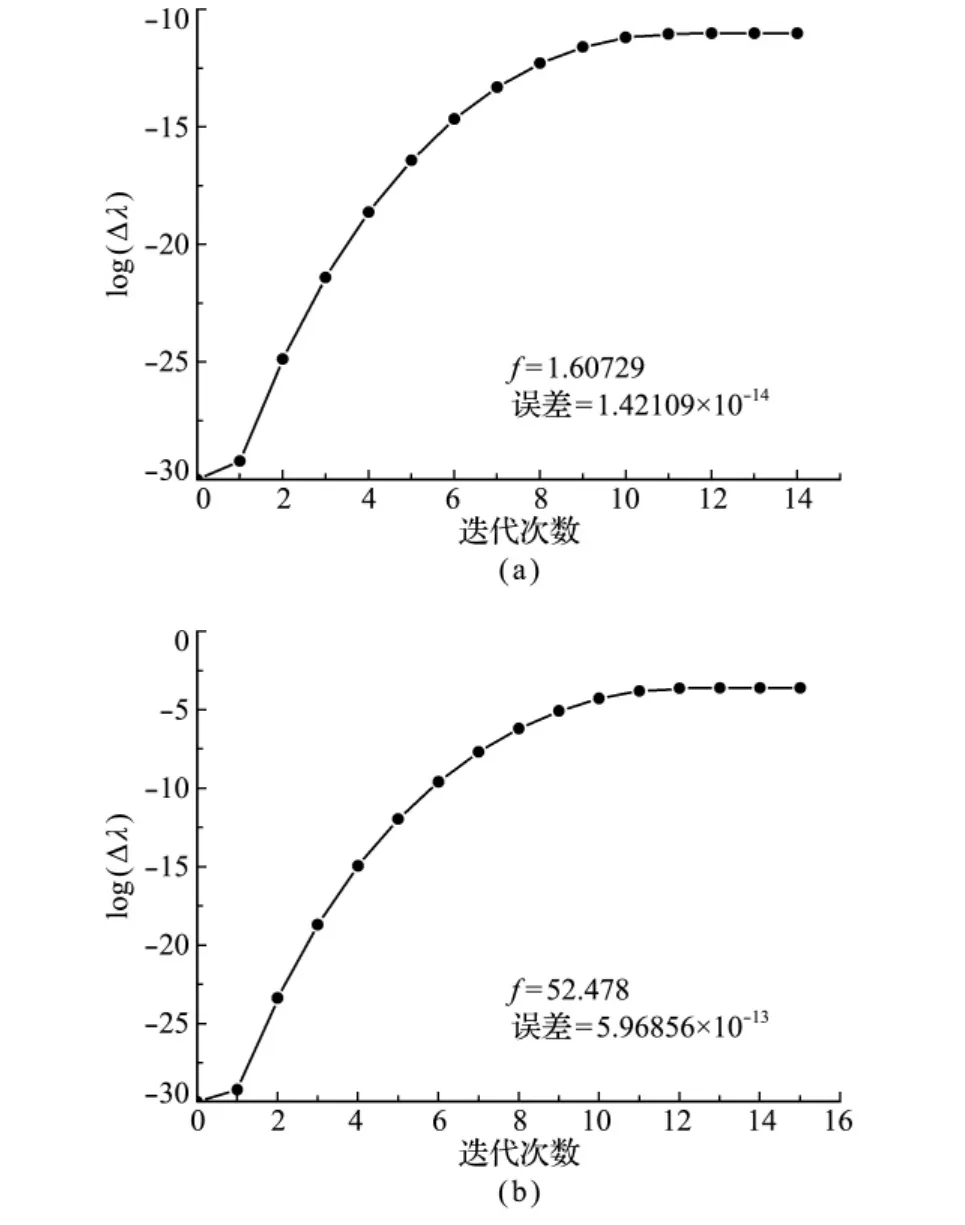
图6 黏塑性因子收敛曲线（m＝5）Fig．6 Convergence profiles on viscoplastic multiplier from the numerical test（m＝5）

5 结 论

（1）对于由弹簧、黏壶和Kelvin链串联而成的黏弹性模型，基于黏弹性蠕变柔度，考虑黏弹性应变历史，假设应力在一个时间步长内线性变化，定义了与弹性问题相对应的与时间增量相关的黏弹性剪切模量和体积模量，导出了增量递推形式的本构方程，可方便地与黏塑性模型耦合计算。增加或减少串联的黏弹性数量，计算程序无需修改，实现了计算程序的通用性。

（2）针对黏弹性和考虑各向同性硬化的双线性型Drucker－Prager屈服函数和Perzyna黏塑性耦合而成的黏弹－黏塑性模型，采用黏弹性预估和黏塑性校正两步算法，考虑算法的收敛和稳定性，把Perzyna黏塑性流动定律转化为与一般塑性问题相对应的一致性条件，建立了黏塑性增量因子单侧逼近于收敛值的 N－R迭代算法，给出黏弹－Perzyna黏塑性耦合模型的完全隐式算法及最终的计算公式，为黏塑性隐式计算提供了一种行之有效的方法。

（3）算例分析表明，对于相同的模型参数和加载条件，应用黏弹性模型计算的变形量最小，黏弹－塑性模型的变形量最大，黏弹－Perzyna黏塑性模型的变形介于两者计算结果之间。随着黏塑性敏感性指数的增大，黏弹－Perzyna黏塑性模型计算的变形量相对减小；当增大到一定值时，其结果接近于黏弹性模型的计算结果。