几何篇:折出点线面体

【编者的话】不深入接触折纸你可能永远也想不通,如此简单的一张白纸能够用来做些什么?折纸有何神奇之处?小时候你折纸可能更加偏重于折些简单的小动物、小物件等,在今天看来,或许已经不那么神奇,但这其实只是你的误解.这次的主题是折纸与数学,自然不那么简单,希望能让你再次惊叹于折纸的无穷魅力.
1、折出定比分点
正方形的纸随意一折,一般能出现一个(凹)九边形,如图1.
如果稍微约束一下随意性,保证折痕经过中心点,那会产生什么奇妙的现象吗?
这个问题很值得研究.
结果发现,如果边的叠合点是各自边上的有理定比分点,那么折痕经过的点也必是某个有理定比分点.从而折叠产生任意的有理定比分点都变得有章可循.
命题 如图2,AD+DC =1,∠C =90。,AB=BC=x.则CD=(1-2x)/(2-2x)
证 由折叠方法可知,AB+BD+DC =1.设CD =y,在△BCD中由勾股定理,x2+y2 =(1-x-y)2.化简为1-2x-2y+2xy =O,从而y=(1-2x)/(2-2x)证毕.
从以上结论看出,如果x是个分母为2n的单位分数(分子为1的分数),即x=1/2n,那么y的值就是(n-1)/(2n-1),说明由B点这个2n等分点,得到了D这个2n-1等分点.
例如要分纸的一边为7等分,那就先把它一组邻边8等分,将两边的第一个等分点叠合起来得到的折痕就过某个7等分点.确切说,这时D是4:3分点.
一般地,对于某个素数N,欲N等分正方形的边,我们必先得到边的N+l等分.因为这是个偶数,所以就只须折叠得到(N+1)/等分.这是较小的一个整数,我们可以继续利用类似的思路,即“偶数÷2,奇数+1”的策略,最终化归得出任何素数的等分点折法.合数的等分点只要依次把每个素数因子等分,就可以实现了.
2 对数螺线怎么折
对数螺线是由笛卡儿在1638年发现的,雅各布·伯努利后来重新研究,他十分惊叹和欣赏这曲线的特性,故要求死后将之刻在自己的墓碑上,并附词“纵使改变,依然故我”.可惜雕刻师误将阿基米德螺线刻了上去,不得不说是一种遗憾,
这是一种神奇的螺线,可以在自然界中找到很多类似的例子,如鹦鹉螺的贝壳、蜘蛛网的构造、漩涡星系的悬臂等.感兴趣的同学,可以阅读《数学文化素质教育资源库》的相关内容,而今天,我们将在常博士的带领下,看看如何用一张普通的纸折出近似的对数螺线.
(一)初步尝试
通过折叠一张纸就能实现初步模拟对数螺线!怎么折?先來学学吧,准备一张A4纸,折起45°角,得到一个等腰三角形,如图1所示.
沿着折痕剪下这个等腰三角形纸片,我们的螺旋折纸就从这个等腰三角形纸片开始.
第一步折叠:沿等腰三角形的中位线,将顶角折向底边.同时注意观察:经过折叠,我们得到的是一个等腰梯形,它的钝角顶点是135°.
接下来我们要折的过程是一系列类似的操作.
先来看第二步折叠如何操作.
这一步的折叠得到的是一个凹六边形.折法是让上底的右端点与下底的中点对合折叠.从效果看,折痕正好与右腰平行,翻转的部分是一个平行四边形.
如图3,折叠示意图中画了圆圈的两点其实可看成是一个大的平行四边形的两个相对的钝角!注意到这个巧合性,我们就感到有趣了!
我们的第三步折叠就是继续将折起来的平行四边形中两个钝角对合折叠.效果如图4.
已经猜到第四步怎么折了?继续叠合上步操作得到的平行四边形的两个钝角.完全正确!你可以操作第五步、第六步、第七步……直至无穷(如果真有那么大的纸张的话).
事实上,另外还限于手工制作的精细度极限,纸变小的过程只能到第十步左右为止.让我们看看电脑绘制的更精细的完成图,如图5所示.
实际上,我们得到了一个类似长裙的裙摆的结构,它像杨丽萍跳孔雀舞时穿的服装,更像是一个摩登的螺旋式台阶的空中俯瞰图.
这款折纸是从台湾的李政宪老师那里学来的,不过稍微加了些变化.
数学上如何看待这个折纸呢?在数学上,我们把每隔一个固定的角度,点到出发起始点的距离就拉伸一个固定的比例,这样的点的运动轨迹叫对数螺线.
在生活中很多地方都有对数螺线的身影:葵花籽在向日葵花头上的排列,鹦鹉螺的壳上的花纹,热带气旋的卫星云图,等等.它们都有统一的数学表达式:p =eaθ.
最后我们来欣赏一下我们的折纸与对数螺旋在多大程度上近似,请看图6.
(二)再次改进
在(一)中,我们尝试着折出了对数螺线的模拟图,但是效果外观并不十分尽如人意,这条螺线与实际的贝壳螺线还有距离.为此,我们还要进一步分析和思考,能否折出如图7中鹦鹉螺那样具有不同参数a的对数螺线p =eaθ的问题.
在这个问题上,日本折纸艺术家布施知子( TomokoFuse)已有一个如图8的设计.她用正方形纸折出顶角为45°的等腰三角形,折痕中有许多平行于底边的平行线.不过她的这些平行线折痕没有充分考虑到螺线的等比性.
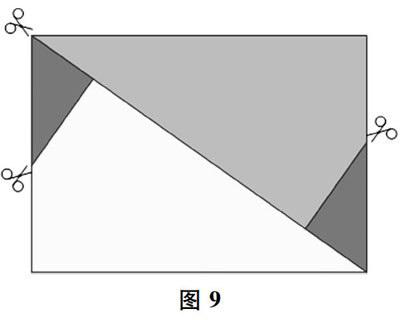
现在我们用数学中等比级数的概念来设计,达到更合乎自然界鹦鹉螺的外观.请先如下列图9所示裁剪A4纸为两个筝形.
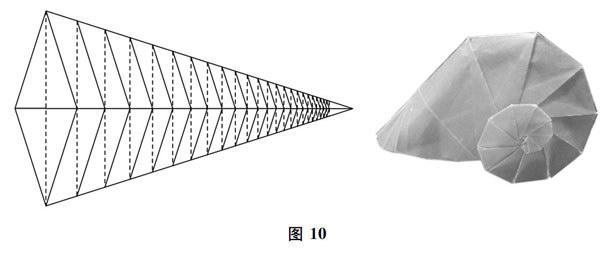
图9裁剪出的两个筝形可以分别独立制作成两个鹦鹉螺.以其中一个为例,折痕图如图10所示.
这些折痕的产生规律是这样的:将筝形的钝角沿着两直角间对角线折向对称轴得到第一条谷线.然后沿着折起的钝角的两边折出两道山折.此后每次折叠都是折这三道折痕的平行线.到末尾阶段可以留一截不再折下去.
在成型阶段,需从锐角顶点开始收.将头上没有折过的地方剪去,然后按预先设计好的山线和谷线来折.形象地说,就是渐渐卷曲使得纸按既定折痕蜷缩成螺的样子.
这个折法真能更完美体现对数螺线吗?
我们不妨来拟合一下这条曲线.先将折纸过程形成的折线绘出.
通过计算机绘图发现图11中的折线与对数螺线二者的差异是很小的.
需要指出的是,采用半张A4纸作为材料只是考虑取材的方便.您完全可以用其他形状的筝形纸片来完成形态各异的螺.
看来,折纸艺术家布施知子的蜗牛经过与数学亲密结合变得更加活灵活现了!
3 从二面角到极小曲面
同学们小时候可能都吹过肥皂泡,而在无数美妙的肥皂泡背后,其实有着不少的秘密.著名的普拉托物理实验是把围成封闭曲线的金属丝放入肥皂溶液中,然后取出来,由于表面张力的作用,在它上面就蒙有表面积最小的薄膜.这种表面积最小的曲面就是所谓极小曲面,从数学上求这膜曲面的问题称为普拉托问题.
极小曲面的应用很广,无论是小到珠宝设计,还是大到建筑设计,都能看到它的身影.
今天,我们会请常博士帮助我们用普通的纸张来折叠组合出一个极小曲面.
我们先从二面角说起,二面角在生活中到处存在,比如墙面总是与地面构成90°的二面角.打开的书本可以形成任意的二面角.人字形的坡面屋顶则一般是大于90°的二面角.此外,三维坐标系由三张平面(xOy,yoz,xOz)两两垂直,形成汇聚在0点的3个90°二面角,在数学上,由三个面构成的多面角称为三面角,
图1就是一个三维立体坐标系的纸模型示意图,它可以用六张正方形的纸折叠插合而成,在这个结构中有八个“三面角”凹陷.
读者可以拿六张统一大小的正方形纸,照如下步骤折一个这样的模型.
方法与步骤:
1.取一张正方形纸,上下两边对折,再把左右两边对折.
2.将一边纸打开并压折,背面折法相同,形成一个双三角结构.
3.重复2中的步骤,再制作五个同样的双三角.
4.将两个插合起来.如图3显示,用一个双三角组合件的一翼插入另一个的一翼之下.
5.在已有的组合结构中添加第三个双三角.如图4,新的双三角要和已有的两个双三角形成互相追赶的效果.如:第一个包裹在第二个中,第二个包裹在第三个中,第三个包裹在第一个中.
小贴士:注意不要插太紧,先看清关系,搭上即可.
6.继续增加双三角到这个结构中,始终注意“A插B,B插C,C插A”的规律,当六个双三角都插在一起后,形成的图案如图5所示.
7.结构雏形出现了,我们用双手从外围四面八方向中心轻轻压,最终就可以形成图1中那个漂亮的立体三维坐标系结构,
现在我们来思考下面的问题:在这世界上,是否还存在类似图1的更简单结构?显然最少的三面角凹陷应该不少于4个,所以首先让我们试着寻找具有4个三面角凹陷的结构.
图6这个结构便是具备了4个三面角凹陷的最简结构,它外轮廓是个正四面体,里面有6个钝角三角形作为连接膜瓣,
如果你拿一个正四面体的铁丝框架浸泡在肥皂液中,拿出框架后就会发现同一结构,这说明这个结构还具有某种最优特征,数学上将肥皂膜形态称为极小曲面.
制作一个这样的纸极小曲面结构,过程比前一个结构还简单.材料都用不到半张A4纸片.
方法与步骤:
1.先照图7中示意裁好8片纸片,其中6片是有用的,有2片多余.
2.取其中一片纸片折出如图8中折痕.其中虚线为谷折,点划线为山折.
3.再制作5片同样的插件.
4.按图9的模式装配起来.
5.适当在插合的地方用些胶水固定,完成.
找到这个结构表明具有凹陷三面角的形态并不孤立,这使我们有了新的期待:是否还有更多的这样的结构呢?读者有兴趣可以继续探索下去.
4 正十二面体:从制作到理解
正十二面体是一种以正五边形为面的多面体,这种不寻常的别致多面体数学内涵非常丰富,柏拉图曾认为我们的宇宙就是正十二面体的,虽然这只是一个美丽的错误,但是正十二面体对于普通大众至今仍充满神秘色彩.
今天,就让我们一起和常博士来探索下正十二面体的折法,以及与正十二面体有关的一个四色问题. (一)制作正十二面体
为了探究正十二面体,我们有必要亲手制作一个.显然,纸模型是最方便的实现方式.
制作正十二面体纸模型的方法很多,这里用组合折纸的方式制作.通过组合拼接而成的结构便于在需要的时候重新调整各面相对位置.
材料:宽度4~5 cm的平行长纸带100 cm.
步骤1 制作一个正五边形的纸带结
用长约8倍宽度的纸带打个结,轻拉两端至最紧,压平(图2左).数学上可以严格证明这个结是正五边形.
步骤2 制作插合正十二面体所需的零件
用长约3倍宽度的纸带折叠一道折痕,使其形成的内角正好符合五边形纸带结的顶角(图2右).
折叠后的纸带重叠区域有一个以36°为底角的等腰三角形.现在请将它的两腰以外的纸带贴着边折到背后,然后再把底边以外的部分剪去(图3).
打开重新将两侧翼藏在夹层内,并且让它们在内部彼此勾起来,压平.我们得到了一个有108°顶角的等腰三角形(图4左).
折叠找到每一腰所对角的角平分线与该腰的交点,将相应锐角折到这个点.可以证明,这两道折痕与三角形三边围成一个正五边形(图4右).
至此我们就完成了第一个插接件.
请再做11个这样的零件.
步骤3 插合正十二面体
每个三角形插接零件上既有榫头也有卯眼:两锐角前端是榫头,两腰靠近顶点的缝隙是卯眼.插合时有一定规则,为了保证这个规则不被破坏,我们给每个插接件上标注一些记号.
作标记的规律:在每片插接件的里侧左下角标为红点榫头,左腰缝隙标为红点卯眼;相应地,右下角为蓝点榫头,右腰缝隙为蓝点卯眼(图5上左).
插合时只要保证榫头插入同色的卯眼(图5上右),就可以顺利完成一个完美的正十二面体(图5下).
(二)探究正十二面體的着色
关于地图的着色有一条著名的定理——四色定理,定理说,任何复杂的地图都可以用不超过四种的颜色给它涂色来区分相邻区域,这条定理至今仍然没有一个简洁的证法,人类对它的认识停留在计算机给出的大规模分类穷举证明,
如果将正十二面体的每个面当成地图上需要区分的一个个区域,则这个特殊的地图确乎需要四种颜色才可以完成以上的着色要求(为什么?).
那么具体怎么着色呢?我们从正十二面体的平面图来看.
想象一个用橡皮绳拉出的正十二面体笼状结构,图6中五边形外轮廓正是其中一个撑开的正五边形洞.换个说法,将笼子的一个五边形洞拉大到可以摊平到桌面的地步,正十二面体就平面化了,必须要记住,这个最大的正五边形轮廓也代表一个面.
我们通过给每一个面标记数字来表示涂色,
图6显示我们将中心标记为1,轮廓(代表相对的被拉大的洞眼)标记为2.
如图7,与1号面毗邻的5个位置选择任意两个不相邻面标记为2,哪两个并无区别,只要旋转就可以统一为图9的样子,
内圈还有3块区域,需要另用3,4来标记,其中涂色方法之一如图8所示.
内圈涂好色后,我们发现外圈中有一块(图9中正上方一块标记为1)是可确定下来的,然后紧接着剩下的4块也被唯一确定,
我们只是给出了其中一种方案,事实上,在数学上可以证明全部的着色方案只有4种.限于篇幅,在此就不赘述了,留给好奇的读者去探索吧!

