异质多智能体系统滞后一致性跟踪控制
李 耿,秦 雯,王 婷,汪 辉, 沈谋全
(南京工业大学 电气工程与控制科学学院,南京 211816)(*通信作者电子邮箱qinwen.wts@njtech.edu.cn)
0 引言
近年来,多智能体系统的分布式协调控制问题引起了不同学科的研究人员的关注[1-3]。一致性问题作为合作控制的最基本问题之一,它要求所有的智能体通过相互交流,让所有智能体的状态趋于一致或者相同。很多研究者从各个角度对一致性问题进行了研究[4-9]。其中,基于领导-跟随者模型的多智能体系统协调控制问题是主要的研究热点之一。文献[10]分别考虑了有无领导者情况下的多智能体系统一致性问题。文献[11]利用分布式观测器研究了领导-跟随者的一致性问题。针对切换拓扑结构,文献[12]研究了带有时滞的多智能体系统的一致性问题。随着深入研究,研究者们发现由于时间延迟的广泛存在,网络中的信息传递通常不是即时的。基于这个考虑,文献[13]提出了滞后一致性的概念。滞后一致性表示跟随者的状态向量落后于领导者一段时间,这使得多智能体系统在有限容量的网络中运动并且不会堵塞。实际上,滞后一致性的现象可以模拟许多实际情况。文献[14]得出了保证领导-跟随者多智能体系统实现滞后一致的充分条件。文献[15]基于相邻智能体的局部信息,提出一种自适应反馈控制算法来实现二阶非线性多智能体系统的滞后一致性。文献[16]提出了利用牵制控制实现二阶多智能体系统的滞后一致性。上述所有的结果都是关于具有相同的动力学模型的多智能体。然而实际应用中,一方面自然界个体和人造工程系统无论在功能上还是结构上都存在差异,智能体的动力学很可能是彼此不同的,比如由于动态系统不同的衰减系数或不同的质量,两个二阶智能体的动力学结构是相同的,但是参数却可能是不同的。另一方面由于群体智能体的共同目的或者通信和执行能力的互异性,耦合智能体的动力学模型可能会不同[17-18],因此研究异构多智能体系统的群集控制具有重大的理论价值和应用前景[19-20]。近年来,越来越多的人关注一类异质多智能体系统——由一阶和二阶智能体组成的混合阶多智能体系统的一致性问题[21-22]。和高阶或者一般混合阶多智能体系统的研究工作相比,混合阶多智能体系统一致性研究的工具和手段不同。一方面,前者由于模型简单,更容易得到比较直观、简单的理论;另一方面,由一阶和二阶智能体组成的混合阶多智能体系统包含有广泛研究结论的一阶智能体系统和二阶智能体系统作为特殊情形。因此,关于混合阶多智能体系统一致性问题的研究具有一定的理论和实际意义。
受文献[16,22]的启发,本文研究领导-跟随者异质多智能体系统的滞后一致性。文献[16]研究了具有动态领导者的二阶多智能体系统的滞后一致性问题,但是所有的智能体拥有相同的动力学模型。本文旨在将文献[16]讨论的结果扩展到由一阶和二阶智能体组成的混合阶多智能体系统的情况。首先,针对由一阶和二阶动力学模型组成的异质多智能体系统,提出一种基于牵制控制的分布式一致性控制协议,来实现异质多智能体系统的滞后一致。通过模型转换,将原始系统转换为等效系统以便进行理论分析。其次,利用图论和Lyapunov稳定性理论证明所设计的协议在固定拓扑结构下是可行的,并且给出了基于线性矩阵不等式形式的充分条件,保证了异质多智能体系统实现领导-跟随者滞后一致性。然后,将得到的结果扩展到切换拓扑结构下的异质多智能体系统的情况。数值仿真验证了所提方法的有效性。
1 预备知识与模型引入
本章介绍了图论知识[23]并引入了模型。
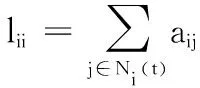
符号说明 本文中,X=diag{x1,x2,…,xn}表示矩阵是以xi为对角元素的对角矩阵。R表示实数集合,Rn是n维欧几里得空间,Rm×n表示m×n维的实数矩阵。Im和0m分别表示m维的单位矩阵和零矩阵。
本文针对智能体系统中个体在动力学上的差异性,将其分为一阶和二阶智能体,研究混合阶多智能体系统的一致性问题。考虑由一个领导者和n个异构跟随者组成的异质多智能体系统,动态领导者表示为:
(1)
其中x0(t)∈Rl和v0(t)∈Rl分别表示动态领导者的位置和速度。
下面给出由一阶和二阶智能体组成的混合阶跟随者。前m个智能体是二阶的,后n-m个智能体是一阶的。异质多智能体系统的方程为:
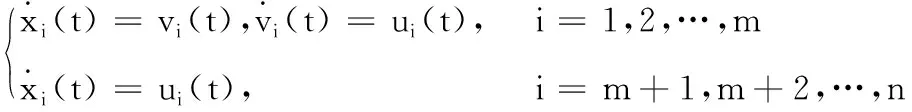
(2)
其中:xi(t)∈Rl和ui(t)∈Rl分别表示跟随者i的位置和控制输入;vi(t)∈Rl代表二阶智能体的速度。
为方便理论分析,本文假设l=1。l>1时相关理论可以用克罗内克积进行推广。
定义1 若存在常数τ>0, 使得:
则称异质多智能体式(1)和(2)能够实现领导-跟随者滞后一致性。
本文研究的目的是基于牵制控制思想设计分布式控制协议,使得异质多智能体系统实现滞后一致性。
2 异质多智能体系统的滞后一致性控制
2.1 固定拓扑下领导-跟随者滞后一致性控制
首先考虑在固定拓扑结构下,拥有动态领导者的异质多智能体系统的滞后一致性。设计基于邻居信息的滞后一致性协议如下:
ui(t)=

(3)
其中:A=[aij]n×n表示固定拓扑图G的邻接矩阵;c1>0,c2>0是控制参数;(x0(t-τ)-xi(t))和(v0(t-τ)-vi(t))两部分是为了使跟随者与动态领导者之间分别实现位置和速度的滞后一致性。本文采用了牵制控制策略。当智能体i能接收到领导者的信息,则bi>0;否则bi=0。 通过协议式(3),带有动态领导者的异质多智能体系统能够达到滞后一致。
注1 本文采用了牵制控制思想,当第i个智能体的节点需要被牵制,则局部反馈增益bi>0。对于大型复杂网络,通常需要通过对所有节点添加控制器来控制它,这样一般是很难做到的,并且花费的价格高昂,而牵制控制可以有效改善这种情况。

将式(3)代入式(2),并整理可得:
(4)

引理1[24]线性矩阵不等式(Linear Matrix Inequality, LMI)为:
其中,Q(x)=QT(x),R(x)=RT(x),它等价于下面的任何一种情况:
1)Q(x)<0,R(x)-ST(x)Q-1(x)S(x)<0。
2)R(x)<0,Q(x)-ST(x)R-1(x)S(x)<0。
定理1 考虑带有动态领导者式(1)的异质多智能体系统式(2),假设固定拓扑下的动态领导者是全局可达点。对于任意的初始状态,如果存在常数c1>0,c2>0和正定矩阵P1满足以下线性矩阵不等式:
(5)
其中E1=
则异质多智能体系统可以实现滞后一致性。

(6)
其中E1=
通过式(4),可将多智能体系统式(1)、(2)的一致性跟踪控制问题的研究转换为分析误差方程式(6)的稳定性。
针对误差系统式(6),选取Lyapunov函数V(t)=yT(t)P1y(t),其中P1是一个正定矩阵。
对V(t)求导得:
(E1y(t))TP1y(t)+yT(t)P1(E1y(t))=

考虑静态领导者的情况,得到以下推论。
推论1 考虑具有静态领导者(v0(t)=0)的异质多智能体系统式(2),假设静态领导者在固定拓扑下是全局可达点。对于任意初始状态,若存在常数c1>0,c2>0和一个正定矩阵P1满足线性矩阵不等式(5),则带有静态领导者的异质多智能体系统式(2)在固定拓扑下能达到领导-跟随者滞后一致。
注2 对于特殊情况v0(t)=0, 领导者是静态的。推论1的证明过程与定理1的证明类似。在此略。
2.2 切换拓扑下领导-跟随者滞后一致性控制算法

对于异质多智能体系统式(2)和动态领导者式(1),设计切换拓扑下基于邻居信息的滞后一致性协议如下:
ui(t)=

(7)

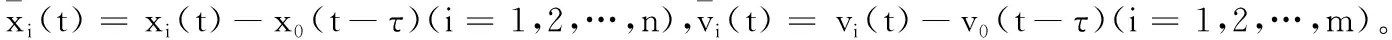
根据式(2)和式(7),可以得到:

(8)

定理2 考虑切换拓扑下带有动态领导者式(1)的异质多智能体系统式(2),假设每个拓扑下的领导者是全局可达点。对于任意的初始状态,如果存在常数k1>0,k2>0和正定矩阵P2满足如下线性矩阵不等式:
(9)
其中σ=1,2,…,N,并且:
则异质多智能体系统能实现滞后一致性。

(10)

经过从系统式(2)到方程组式(8)的转化,并把系统式(8)转换为与误差向量y(t)有关的方程式(10),将对多智能体的一致性分析转化为对误差系统式(10)的稳定性分析。
在切换拓扑下,根据误差系统式(10)选取Lyapunov函数V(t)=yT(t)P2y(t), 其中P2是正定矩阵。
对V(t)求导得:
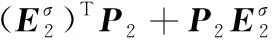
推论2 考虑切换拓扑下具有静态领导者(v0(t)=0)的异质多智能体系统式(2),假设静态领导者在每个拓扑下是全局可达点。对于任意初始状态,若存在常数k1>0,k2>0和一个正定矩阵P2满足线性矩阵不等式(9),则带有静态领导者的异质多智能体系统式(2)在切换拓扑下达到领导-跟随者的滞后一致。
注3 如果τ=0, 那么得出的结论与文献[22]类似,即跟随者可以与领导者达到完全的恒同一致。
3 数值仿真
在本章中,采用数值例子来验证理论算法的有效性。
例1 考虑固定拓扑下带有动态领导者式(1)的异质多智能体系统式(2)在一维空间的情况。

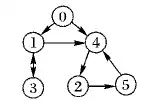
图1 6个智能体之间的固定拓扑图Fig. 1 Fixed topology graph between six agents
由图1可以得到以下的邻接矩阵A和B:
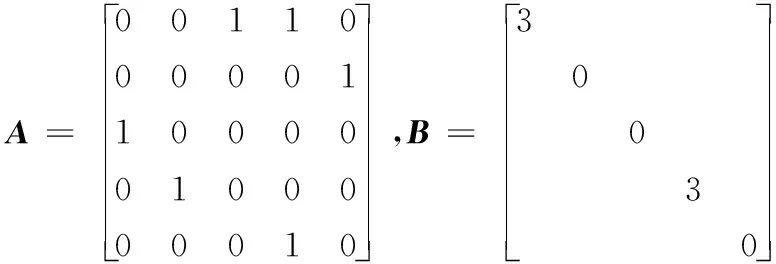
易证明,选择参数c1=1,c2=1,τ=6可以满足定理1的条件,并通过Matlab中LMI工具箱可以得到LMI式(5)的解如下正定矩阵:

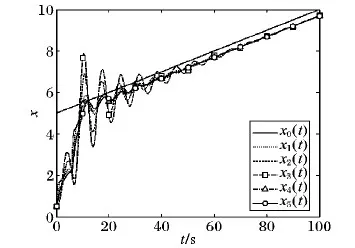
图2 固定拓扑下异质多智能体的位置轨迹Fig. 2 Position trajectory of heterogeneous multi-agent under fixed topology
图2中的xi(t)(i=1,2,3)表示二阶智能体的位置轨迹,x4(t)、x5(t)表示一阶智能体的位置轨迹。从图2可知,当时间到达60 s以后,跟随者与领导者达到滞后一致。图3表明滞后位置和速度误差渐近收敛到0,也就是说,用设计的协议式(3)可以使异质多智能体系统在固定拓扑下实现领导-跟随者滞后一致性。

图3 固定拓扑下的滞后位置误差和滞后速度误差Fig. 3 Lag position error and lag velocity error under fixed topology
情况2 考虑1个领导者和8个跟随者组成的多智能体系统,全局可达的领导者标记为0,二阶智能体标记为1、2、3、4和5,一阶智能体标记为6、7和8。
从图4可知,8个跟随者跟踪上了领导者并且始终滞后领导者τ=6 s时间,即达到滞后一致性。

图4 固定拓扑下8个智能体滞后跟踪领导者的位置轨迹Fig. 4 Position trajectory of eight agents lag tracking leader under fixed topology
例2 考虑切换拓扑下带有动态领导者式(1)的异质多智能体系统式(2)在一维空间的情况。


图5 三种可能的拓扑图Fig. 5 Three possible topologies
容易证明通过选择k1=1,k2=1,τ=2可以满足定理2的条件,并利用Matlab求得LMI式(9)的解:
其中正定矩阵P2是对应于3个切换拓扑结构时LMI的共同解。仿真结果如下:图6表示了跟随者的位置轨迹滞后领导者一段时间τ=2。图7表明滞后位置和速度误差渐近收敛到0,即用设计的协议式(7)可以使带领导者的异质多智能体系统在切换拓扑下达到滞后一致。
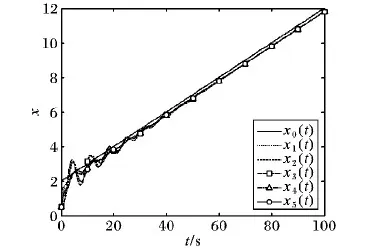
图6 切换拓扑下异质多智能体滞后跟踪领导者的位置轨迹Fig. 6 Position trajectory of heterogeneous multi-agent lag tracking leader under switching topology
注4 本文考虑了更加符合实际应用的滞后一致性的情况。汽车行驶过程中,如果让领头的车辆先行,后面跟随的车辆与领头的车辆保持一定的滞后,这样就可以缓解拥堵的情况。本文将文献[21]中结论扩展到滞后一致性的情况,并在例子中扩大了智能体的规模,更有效地验证了分布式控制。相比于文献[21]让所有跟随者能获得领导者的速度信息,本文只让部分跟随者获得领导者的位置和速度信息。

图7 切换拓扑下的滞后位置误差和滞后速度误差Fig. 7 Lag position error and lag velocity error under switching topology
情况2 考虑9个节点组成的多智能体系统。全局可达的领导者标记为0,二阶智能体分别标记为1、2、3、4和5,一阶智能体分别标记为6、7和8。

图8 切换拓扑下8个多智能体滞后跟踪领导者的位置轨迹Fig. 8 Position trajectory of eight agents lag tracking leader under switching topology
注5 由于智能体之间的信息传输中常存在通信时延,下面考虑通信时延为0.001 s,得到仿真结果如图9所示。

图9 带有通信时滞的异质多智能体滞后跟踪领导者的位置轨迹Fig. 9 Position trajectory of heterogeneous multi-agent lag tracking leader with delay in communication
从图9可以看出,当系统存在通信时延时,采用本文的控制协议可以使多智能体实现领导-跟随者滞后一致性。
4 结语
针对异质多智能体系统的滞后一致性问题,本文提出了基于牵制控制思想的分布式一致性控制协议。基于Lyapunov稳定性理论和图论,给出了在固定拓扑和切换拓扑下实现领导-跟随者滞后一致性的充分条件。数值仿真验证了在固定拓扑和切换拓扑下的理论算法的有效性。本文考虑了动态领导者速度已知的情况,但是在更一般情况下,跟随者不能获得领导者的速度,另外,实际智能体之间的通信延时是不可避免的情况,在今后工作中,我们将设计分布式控制协议,考虑带有通信时延和宽带受限因素,研究领导者速度未知情况下多智能体系统滞后一致性。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

