Neumann边界下的反应项非局部扩散方程爆破研究①

张敏华

(福州大学阳光学院,福建 福州 350015)

0 引 言

反应扩散方程理论是现代数学中重要的组成内容，在空间上普遍存在着非局部作用。人们通过卷积算子可以对生态系统以及材料科学领域中空间上的非局部作用进行描述，这就是所谓的非局部扩散方程。非局部性使得反应扩散方程更为复杂化，众多研究学者对于反应非局部方程的行波解、稳定性、爆破以及熄灭等方面进行了大量的研究[1]。

1 文献综述

(1)

国内众多研究学者也对非局部扩散方程的爆破解进行了研究，王玉兰对非局部扩散方程(2)，方程中的m和p大于0和1，在光滑连通区域内的方程存在有限时刻爆破解[4]；杜宛娟与裴海杰同样对上述类似的方程在Neumann边界条件下的爆破进行研究证明非负非平凡的解在有限时间T内爆破，并对解的生命跨度进行了估计和确定了爆破速率为1/k[4]；

(2)

韩玉柱等人通过采用积分不等式对扩散方程的初值假设条件进行了弱化处理证明了正解存在全局爆破性质并对爆破集进行了估计，并对Neumann边界条件下的带有反应项的非局部扩散方程(3)进行了爆破研究，通过研究证明指出当p大于1时非负非平凡解在有限石刻爆破[5]。

(3)

基于此，探讨带有指数型反应项的非局部扩散方程如(4)所示，

(4)

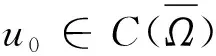
(5)

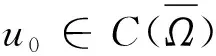
T

(6)

定理3： 假定u是问题(4)的解，并在在时刻T爆破，那么解的爆破时间则可以用公式(7)表示，如下所示。

(7)

2 解的局部存在性、唯一性与比较原理

2.1 解的局部存在性、唯一性

那么可以明显看到方程的解正好是映射在某一个球形区域的不动点。在对定理1进行证明之前，需要使用到引理1。

引理1： 假定非负函数u0，v0，且u、v均属于Xt0，那么就存在一个正的常数C=C(k,||u||Xt0,||v||Xt0,||J||l∞,Ω)使得‖Tu0(u)-Tv0(v)‖Xt0

u(x,t)-u0(x)

通过对x变量在区域Ω上进行积分并采用Fubini定理即可以得到如下(8)所示，由此定理1得以证明。

(8)

2.2 比较原理

(9)

下解的定义方式与上解相同，仅仅只需要将式(9)中的≥符号全部更换成≤即可为对下解进行定义。为了得到方程(4)的比较原理，则需要引入极值定理的两个引理。

引理2的证明如下所示：假定在某些点处u(x,t)为负，即认为u(x,t)小于0。此时令θt(x,t)=e-λtu(x,t)(λ>0,λ≥2sup|c|)，假设在(x0,t0)点时θ达到负的最小值时，那么就有t0大于并且有

θt(x,t)=-ke-kt0u(x0,t0)+e-kt0ut(x0,t0)≥

这与前面假定的θ在点(x0,t0)处产生负的最小值的假设存在矛盾性，则证明了当θ(x,t)大于等于0时，就有引理2的结论。

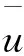
3 全局存在与爆破

定理2的证明：方程(4)的第一个方程的变量x在区域Ω上积分，并应用Fubini定理和Jensen不等式则可以得到如下(10)所示的不等式。

(10)

通过对(10)不等式进行变量t进行两边积分即可以得到对解的爆破时间估计有T即定理2得以证明。

定理3的证明：假定T<是方程爆破解存在的最大时间，并且使得

(11)

对上述不等式(11)在(t,T)上进行积分便可以得到下式(12)

(12)

(13)

让ε无限趋向于0，根据(12)和(13)就可以得到定理3的爆破时间的结论。由此对具有指数反应项的非局部扩散方程在Neumann边界条件下解的局部性、唯一性以及解的爆破时间估计与爆破时间等爆破性质全部得以证明。

4 结 论

非局部扩散问题是高等数学研究的难点内容，尤其是对非局部扩散方程的爆破性质的探讨是研究的热点。基于此，对具有指数反应项的非局部扩散方程进行了解的局部性、唯一性以及爆破生命估计等爆破性质进行讨论且以上爆破性质均得到了证明。研究结论显示，非局部扩散方程的非负非平凡的解在有限时刻爆破，并推导了爆破时间与估算了爆破生命长度。