基于非对称阿基米德Copula模型的投资组合风险度量

王 沁, 吕王勇

(1. 西南交通大学 数学学院, 四川 成都 610031;2. 四川师范大学 数学与软件科学学院, 四川成都 610066)

自20世纪90年代以来,随着金融全球化、一体化的进程,国际金融领域已发生了多次的金融危机,如欧洲汇率体系危机、东南亚货币危机、美国次贷危机、俄罗斯卢布危机等,这迫使人们不得不更加重视对金融风险的管理.由于风险价值(VaR)能够在一定置信水平下,把金融资产组合在一定时期内最大可能损失定量化,是一种既能处理非线性问题又能概括证券组合市场风险的工具,成为度量金融风险的一种普遍使用的工具.

作为多元统计分析以及相关性分析的工具,Copula理论很自然地被引入金融风险管理的研究中.利用Copula-GARCH模型来计算投资组合的风险价值,不仅可以描述资产收益率尖峰、厚尾的分布特征和异方差波动的特点,还可以捕捉资产之间的非线性相关关系.较先将Copula引入金融风险管理的是Embrechts等[1-3]引入了动态Copula来计算VaR,随后许多学者对这一领域进行了更加深入的研究[4-8].针对国内金融市场,国内学者也对Copula理论在金融风险投资组合的研究方面做了一些尝试.吴振翔等[9]基于阿基米德Copula对组合风险进行了测度与研究;张金清等[10]从拟合优度出发,基于Copula模型研究资产组合的集成风险;周孝华等[11]结合SV模型与GPD分布,利用Copula模型分析了投资组合风险；李明等[12]基于Clayton Copula度量了金融风险；杜子平等[13]从混合藤Copula模型,对资产组合VaR计算精度方面进行了比较.总之,Copula模型简单易操作,相比于传统的金融风险管理模型,有利于测量风险、将风险定量化,更具有实用性和参考价值.

在计算二维投资组合的VaR值时,一般都选择Clayton-Copula、Gumbel-Copula和Frank-Copula等3类阿基米德Copula来反映投资组合变量之间的相关特征.由于Clayton-Copula用于描述变量在下尾处具有较强的正相关关系的现象,Gumbel-Copula只能用于描述变量间上尾高下尾低的非负相关关系的现象,Frank-Copula用于描述变量间的负相关和正相关关系,但只能捕捉变量间的对称的上下尾部相关性；所以,这3类阿基米德Copula存在缺陷,而且所有的二元阿基米德Copula都具有结合性和对称性的特点.基于此,本文对阿基米德Copula进行改进,引入几何平均和加权平均的结合,构造非对称的加权混合阿基米德Copula模型来描述投资组合变量之间的相关特征,并以此为基础结合蒙特卡洛模拟方法计算二维投资组合的VaR值,与已有的VaR计算方法进行比较，验证其精确性.

1 各类Copula函数的基本知识

二元正态Copula模型为

其中ρ为线性相关系数,|ρ|<1.二元正态Copula模型的上尾相依指标、下尾相依指标[2]分别为

二维T-Copula函数为

其中ρ为线性相关系数,|ρ|<1.二维T-Copula模型的上尾相依指标、下尾相依指标[2]分别为：

二维Clayton-Copula函数为

Cc(u,v,α)=φ[-1](φ(u)+φ(v))=

其中α∈[-1,){0}.二维Clayton-Copula模型是阿基米德Copula模型[2],其生成元上尾相依指标、下尾相依指标分别为：

二维Frank-Copula函数为

其中α≠0.二维Frank-Copula模型是阿基米德Copula模型,其生成元上尾相依指标、下尾相依指标[2]分别为

2个Copula函数的加权平均仍是Copula函数[2],即如果C1(u,v,θ1)和C2(u,v,θ2)是2个不同的Copula,那么

C(u,v)=αC1(u,v,θ1)+(1-α)C2(u,v,θ2)

也是Copula函数.如果C1(u,v,θ1)是正态Copula函数,C2(u,v,θ2)是阿基米德Copula函数,那么它们的加权平均Copula函数具有对称性的特点,而且上尾相依和下尾相依指标仅仅由阿基米德Copula函数决定.如果C1(u,v,θ1)是T-Copula函数,C2(u,v,θ2)是阿基米德Copula函数,那么它们的加权平均Copula函数也具有对称性的特点.如果C1(u,v,θ1)和C2(u,v,θ2)是阿基米德Copula函数,那么它们的加权平均Copula函数具有结合性和对称性的特点.结合性和对称性的特点并不符合金融市场变量的相依关系.

2 非对称的加权混合阿基米德Copula模型

为了克服这类加权平均Copula函数结合性和对称性的特点,引入几何平均和加权平均的结合,构造非对称的加权混合阿基米德Copula模型(简记为AWH阿基米德Copula模型),该模型为

CAWH(u,v)=αCA1(u,v,β1)+

(1-α)u1-λ1v1-λ2CA2(uλ1,vλ2,β2),

(1)

其中α∈(0,1]是加权平均的系数,体现了2类Copula模型相互混合的特点.

λ1∈[0,1],λ2∈[0,1]

是几何平均的权重,体现了非对称的特点.

由于AWH阿基米德Copula模型是加权平均,具有凸结合的特点,CA1(u,v,β1)可以选择阿基米德Copula,也可以选择椭圆类Copula等各种类型的Copula.为了分别反映投资组合变量在上尾和下尾具有不同的相关关系,将BB1-Copula(又称广义Clayton-Copula[14])作为CA1(u,v,β1),其表达式为

(2)

其中,参数

β1={(θ,δ)|θ>0,δ>1}.

BB1-Copula模型实际是一类双参数的阿基米德Copula模型,其生成元为

φδ(t)=[(t-θ-1)]δ, δ>1,θ>0.

(3)

下尾相关关系

上尾相关关系

定理1[15]当λ1∈[0,1],λ2∈[0,1]时,CA2(u,v,β2)是阿基米德Copula模型,那么

CAS(u,v)=u1-λ1v1-λ2CA2(uλ1,vλ2,β2)

是一类Copula模型.证明参见文献[15].

当λ1≠λ2时，

CAS(u,v)≠CAS(v,u).

(4)

因此,当CA2(u,v,β2)是阿基米德Copula模型,λ1∈[0,1],λ2∈[0,1],CAS(u,v)是一类由阿基米德Copula衍生出来的非对称的Copula.当λ1=λ2=1,CAS(u,v)为一类阿基米德Copula;当λ1=λ2=0,CAS(u,v)为相互独立的乘积Copula.当λ2+λ1≤1时,

即当λ2+λ1≤1时,CAS(u,v)不能用于描述在下尾处具有较强相关关系的现象.

AWH阿基米德Copula模型由CA1(u,v,β1)与CAS(u,v)的凸结合构成,其中CA1(u,v,β1)描述了二维变量之间上下尾部相关性,CAS(u,v)描述了二维变量之间不对称的特点,所以,通过几何平均和加权平均的结合,AWH阿基米德Copula模型非常符合金融变量之间的相依特征.

3 基于非对称阿基米德Copula模型仿真计算VaR

风险测量方法VaR在监管等领域获得广泛应用,成为金融市场风险测量指标的主流.确切地说,VaR可表示为

Prob(ΔP≤VaR)=α，

其中Prob表示资产的损失小于可能损失上限VaR的概率；ΔP表示证券组合在持有期Δt内的损失；α表示风险测量的置信水平.假设金融资产组合有2种资产X、Y,其收益为x、y.组合中它们所占的比例为ω、1-ω,2种金融资产收益的Copula函数为C(u,v),则VaR可以利用下式来计算

P(ΔP≤VaR)=P(ω·x+(1-ω)·y≤VaR)=

(5)

r(t)=μ+ε(t),

ε(t)=h(t)1/2e(t),

(6)

其中,w>0,αi≥0,i=1,L,q,βi≥0,i=1,L,p,ε(t)为独立同分布的残差序列,Eε(t)=0,Dε(t)=1.当q=p=1,e(t)服从标准正态分布,称为GARCH(1,1)-Normal模型.当q=p=1,e(t)服从标准T分布,称为GARCH(1,1)-t模型.当q=p=1,e(t)服从广义误差分布,称为GARCH(1,1)-GED模型.

根据Copula函数计算组合VaR表达式(5)的解析表达不易求出.因此,实际研究中,通常结合Mente Carlo与Copula函数法计算VaR,具体计算步骤如下：

Step 1:边缘分布建模.建立描述资产X和Y收益率序列的边缘分布的GARCH(p,q)模型,通过GARCH(p,q)模型计算边缘分布函数FX(·)和GY(·),并将边缘分布转化为均匀分布.

Step 2:AWH阿基米德Copula模型参数的估计.基于利用均匀分布的历史数据,利用极大似然估计Copula模型的参数.AWH阿基米德Copula模型的对数似然函数可表示为

lng(ynt|θ)+lnc(F(x|θ),G(y|θ)),

(7)

其中

根据极大似然估计的性质,参数向量θ=(β1,β2,α,λ1,λ2)满足

由上面的约束条件得到AWH阿基米德Copula模型的权重(α,λ1,λ2)和Copula参数(β1,β2)的极大似然估计.

Step 3:模型选择：AWH阿基米德Copula模型中的CA2(u,v,β2)可以选择不同的阿基米德Copula模型,所以,需要进行模型的选择,确定CA2(u,v,β2)是哪一个阿基米德Copula模型.本文采用AIC值最小原理进行模型的选择.AIC值的计算公式为

AIC=-2ln(模型的极大似然度)+

2(模型的独立参数个数).

Step 4：随机模拟产生服从AWH阿基米德Copula模型的随机数.AWH阿基米德Copula模型的Monte Carlo仿真通过条件采样来实现的[2].

1) 产生2个相互独立的服从[0,1]区间均匀分布的随机变量(u1,w)；

2) 分别计算

和

的伪逆函数,并将随机变量w代入得

实现条件采样.那么,(u1,v1)和(u1,v2)为服从CA1(u,v,β1)和CA2(u,v,β2)的二维随机变量的随机数.

3) 产生2个相互独立的服从[0,1]区间均匀分布的随机变量(u3,v3),然后计算

那么,(u4,v4)为服从

CAS(u,v)=u1-λ1v1-λ2CA2(uλ1,vλ2,β2)

的随机数.

4) 计算

(u,v)=α×(u1,v1)+(1-α)×(u4,v4)

得ASH阿基米德Copula模型的Monte Carlo仿真数据.

Step 5：计算投资组合的收益率L的值.根据各资产收益的GARCH(p,q)模型,计算与u、v对应的资产收益率x、y的值

给定资产x在投资组合的权重ω,计算投资组合的收益率L的值；L=ωx+(1-ω)y.由此得到投资组合未来收益的一个可能情形.

Step 6：计算VaR值.重复Step4和Step5m次,得到已定投资组合未来收益的m个可能情形,由此可以得到其经验分布,对于给定的置信水平α,由α水平分位数即可得到投资组合的VaR值,即Prob(ΔP≤VaR)=α.

LLR=-2ln[(1-p*)T-Np*N]+

2ln[(1-N/T)T-N(N/T)N].

(8)

在原假设p=p*的条件下,统计量LLR服从自由度为1的χ2分布.若LLR≤χ2(1),接受原假设,即可以认为被检验模型可以很好的拟合样本数据；相反地,若LLR>χ2(1),拒绝原假设,则说明被检验模型并不能很好的拟合样本数据.

4 实证分析

选择大连圣亚、三特索道2只旅游行业的股票,考察旅游业作为金融投资组合的风险价值.时间跨度为2013年01月04日至2014年12月31日,构造样本数据对(xi,yi)：

1) 基本统计特征.大连圣亚和三特索道各自收益率的线图及描述性统计结果如图1和表1.

图 1 大连圣亚和三特索道各自收益率的线图

样本均值样本标准差样本偏度样本峰度JB统计量服从正态分布大连圣亚(DL)0.000 8240.024 1200.483 9857.914 781497.658 8不服从三特索道(ST)0.001 0250.020 5400.251 3496.034 389187.627 7不服从

从图1和表1中可以看出大连圣亚和三特索道的平均收益率差异不大,它们的偏度都大于零,峰度都大于3.2个收益率序列表现出显著的尖峰、厚尾,不服从正态分布的统计特征,而且存在时变方差特征.因此,引入GARCH类模型来描述其波动特征.

2) 边缘建模.分别利用GARCH(1,1)-Normal、GARCH(1,1)-t和GARCH(1,1)-GED模型对大连圣亚收益率、三特索道的收益率进行拟合,相应的参数和AIC值如表2.

表 2 大连圣亚和三特索道收益率的各类GARCH模型

通过AIC值比较以及参数的显著性检验可知,GARCH(1,1)-t模型可以较好地描述各个收益率序列的波动.利用所得模型的结果分别对原序列进行概率积分变换,将随机变量(X,Y)的边缘分布转化为服从(0,1)均匀分布,变换后的变量记为(U,V).图2和表3是运用Q-Q检验和K-S检验方法检验的结果.

图 2 GARCH转化后的Q-Q检验图

大连圣亚收益率变换后序列X1三特索道收益率变换后序列Y1K-S统计量概率值K-S统计量概率值0.026 20.891 40.033 20.727 9

表3的K-S统计量与概率值表明,对原序列进行概率积分变换后的序列都服从(0,1)均匀分布,这进一步说明GARCH(1,1)-t模型可以较好地描述各个收益率序列的波动.

3) 参数估计及Copula函数的选取.利用组合序列(ut,vt)结合 Matlab软件对凸结合构成的混合Copula模型

C(u1,u2)=α1Ck1(u1,u2,θk1)+

(1-α1)Ck2(u1,u2,θk2)

进行参数进行估计,结果如表4.

从表4可以看出,Clayton-Copula与Frank-Copula所构成的混合Copula模型的AIC值最小,所以,选用Clayton-Copula与BB1-Copula的几何平均与加权平均结合AWH阿基米德Copula模型,以及Frank-Copula与BB1-Copula的几何平均与加权平均结合AWH阿基米德Copula模型进行分析与研究.

表 4 混合Copula模型参数估计及AIC值

4) AWH阿基米德Copula模型的参数估计.利用组合序列(ut,vt)结合Matlab软件对AWH阿基米德Copula模型

CAWH(u,v)=αCA1(u,v,β1)+

(1-α)u1-λ1v1-λ2CA2(uλ1,vλ2,β2)

进行参数进行估计,结果如表5.

表 5 ASH阿基米德Copula模型的参数估计及AIC值

从表5可以看出,Clayton-Copula与BB1的几何平均与加权平均结合ASH阿基米德Copula模型的AIC值比较小,而且权重λ1≠λ2,所以,该模型捕捉了数据的非对称特点,以及上尾与下尾的相依机制.

5) 根据得到的ASH阿基米德Copula模型,运用Copula模型与Monte Carlo仿真.首先产生476个服从参数为0.416 15和1.273 62的BB1-Copula模型的随机数列(u1,v1),产生476个服从参数为0.642 42的Clayton-Copula模型的随机数列(u1,v2),产生476个服从参数为独立同标准均匀分布的随机数列(u3,v3),计算

则(u4,v4)为服从

CAS(u,v)=u1-λ1v1-λ2CA2(uλ1,vλ2,β2)

的随机数.令

(u,v)=α(u1,v1)+(1-α)(u4,v4),

得AWH阿基米德Copula模型的Monte Carlo仿真数据.

6) 利用Monte Carlo仿真数据(u,v),结合边缘Garch-t(1,1)模型GARCH求得其原函数序列(x′,y′),即(x′,y′)为由Monte Carlo模拟得到的收益率序列.为了简化计算,本文取2支股票的持有权重各为0.5,则可以得出投资组合在其持有期(t-1,t]内的组合损失率为

表 6 实际序列与仿真序列的统计量

由表6中实际序列与仿真序列统计量对比可以看出,原始数据的指标与模拟数据基本保持一致.因此,Clayton-Copula与BB1-Copula的AWH阿基米德Copula模型可以很好的刻画实际收益率序列,可以运用此模型计算单个资产以及投资组合VaR的值.

7) 选定置信度为1-α=95%,利用仿真序列预测下一时刻2支股票及其投资组合的VaR结果如表7.

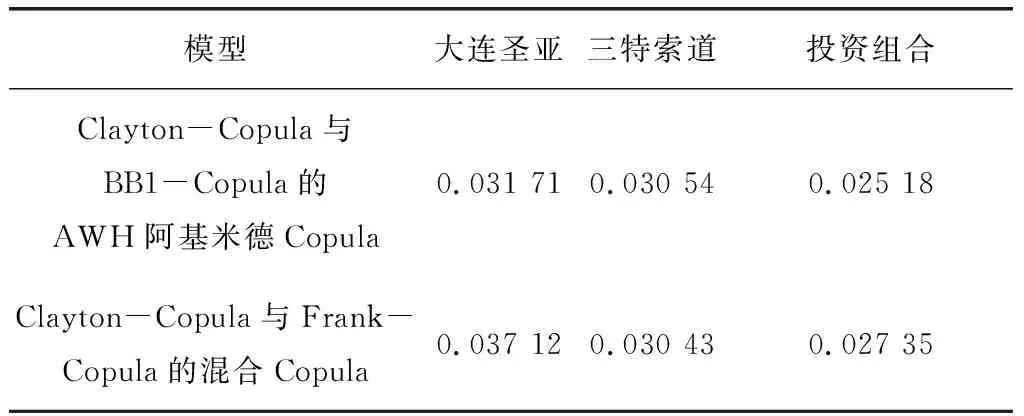
表 7 单支股票及其投资组合VaR

可以看出,AWH阿基米德Copula仿真序列的VaR为0.025 18,Clayton-Copula与Frank-Copula的混合Copula仿真序列的VaR为0.027 35,也就是说由于对称性的特点,Clayton-Copula与Frank-Copula的混合Copula存在低估VaR的特征.

2ln[(1-N/T)T-N(N/T)N].

经计算,

相对于Clayton-Copula与Frank-Copula的混合Copula,其失败次数N=24,相应的

此结果充分说明计算出的VaR具有较好的准确性及有效性,进而说明根据原始收益率估计得到的Copula模型可以很好地刻画实际收益率序列.

5 结论与展望

1) 本文从加权平均和几何平均的角度,构造了非对称的加权混合阿基米德Copula模型,体现了2类阿基米德Copula模型相互混合的特点,较为准确地描述变量之间非对称和尾部相关性.

2) 通过比较非对称的加权混合阿基米德Copula模型,与凸结合的混合Copula模型所得的AIC值,可以看出,非对称的加权混合阿基米德Copula模型能更细致描述不同金融资产之间的非线性的、非正态的、尾部风险不对称的相依关系,为市场参与者,尤其是监管机构、投资机构等市场主体提供了防范和抵御极端金融风险的理论方法.

3) 本文利用非对称的加权混合阿基米德Copula模型对金融投资组合的风险价值进行了分析,实证结果显示Clayton-Copula与Frank-Copula的混合Copula模型的风险价值过低,而基于非对称的加权混合阿基米德Copula模型保证了随机变量之间非对称特性,具有较好的准确性及有效性.