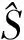一种估计高维协方差矩阵的新方法

(山东师范大学数学与统计学院，250358，济南)

1 引 言

随着信息技术和计算机技术的飞速发展，越来越多的高维数据出现在我们的生活中.在许多统计应用中，总是存在需要处理高维数据的情况.在以前的多维统计结论中，我们通常假设观测样本的数目n足够大.但是，在许多情况下，数据的维数p大于样本量n，这种情况通常被称为“大p小n”.在这种情况下，一些传统的统计结论将不再成立.例如，在判别分析中，当总体协方差矩阵未知时，需要用样本协方差矩阵的逆矩阵来代替判别函数中总体协方差矩阵的逆.另外，在协方差矩阵相等的相关检验中，一些传统的检验统计量要求样本协方差矩阵具有可逆性.但是在“大p小n”的情况下，样本协方差矩阵不可逆的概率为1.因此，一些专家尝试用其他方法进行假设检验，如修正似然比方法[1-4]；非参数方法等[5-6].

从上述两个例子中，我们可以看到，在许多应用中，我们都需要样本协方差矩阵是可逆的.然而，在“大p小n”的情况下，传统的样本协方差矩阵是不可逆的.本文试图给出一种利用变量间的特殊关系估计协方差矩阵的新方法，即在“大p小n”条件下，协方差矩阵仍然是可逆的.在许多实际情况中，变量之间存在一些特殊的关系.其中，条件独立性是一种非常重要的关系，在图模型的学习中起着重要的作用.对于多元正态分布的变量，如果变量之间存在条件独立关系，则样本协方差矩阵和精度矩阵具有特殊的结构.

本文通过条件独立正态模型下协方差矩阵和精度矩阵的特殊结构，给出了估计协方差矩阵的新方法，使得新估计在高维的情况下仍是可逆的.本文的结构如下：第一部分给出了相关引理和重要结论；第二部分我们给出了一种估计协方差矩阵的新算法使得得到的新估计具有较强的可逆性；最后一部分通过数值例子验证了新方法的有效性.

2 预备知识

假设随机向量X～Np(0,Σ),向量X分为k个部分，即X=(X1′,X2′,…,Xk′)′,其中Xi′是pi维的

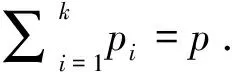
以下结构[7]：

(1)

在精度矩阵的这种结构下，协方差矩阵∑具有以下结构：

(2)

这个模型是Anderson和Perlman于1993年提出的Lattice Conditional Independence(LCI)模型[8]的一个特殊情形.我们在接下来的内容中主要考虑k=3的情况.在k=3的情况下，精度矩阵具有以下结构：

(3)

并且协方差矩阵具有以下结构：

(4)

定义1[9]设X～Np(0,Σ).令x1,x2,···,xn是一个随机样本，则传统的样本协方差矩阵定义如下：

(5)

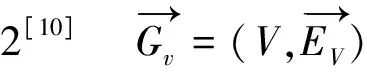
i)C∪A∪B=V;

ii)A⊥B|C.

在因果强分割(C,A,B)中，我们把变量集C称为因果强分割集.

对于寻找变量之间的条件独立性,我们有如下的算法1.

算法1[10]因果强分割搜索算法.

输入：样本集D,变量集V; 输出：因果强分割(C,A,B).

步骤1：找出因果强分割(C,A,B).

for每对{u,v}⊂Vdo else ifA⊥B|C∪{w}then

for 每个V′⊂V{u,v}doC={w}∪C

ifu⊥v|V′then for每个变量s∈Cdo

V′=V′ if∀u∈A,∃C′⊆C{s}使得s⊥u|C′then

end ifC=C{s},B={s}∪B

end for else if∀v∈B,∃C′⊆C{s}使得s⊥v|C′then

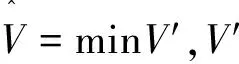
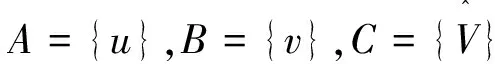
把V中的变量逐个移到A,B,C中 break

for 每个变量w∈Vdo end for

if ∀u∈A,∃C′⊆C使得w⊥u|C′then else

B={w}∪Bbreak

break end for

else if∀v∈B,∃C′⊆C使得w⊥v|C′then return(C,A,B)

A={w}∪Aend for

break

步骤2：找出A与B的变量个数相差最小的因果强分割(C,A,B).

for 每个因果强分割(C,A,B)do

Φj=||Aj|-|Bj||

end for

return(C,A,B)=argminΦj

3 估计高维协方差矩阵的算法

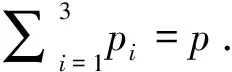
(6)

令x1,x2,…,xn是一个随机样本，则新的协方差矩阵的估计定义如下：

(7)

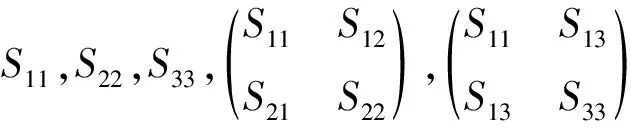
算法2 估计高维协方差矩阵的算法.

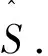
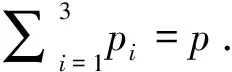
if dim(X1,X2)≤n且dim(X1,X3)≤nthen样本协方差矩阵结构为

else if dim(X1,X2)>n且dim(X1,X3)>n

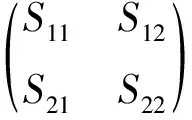
else if dim(X1,X2)>n

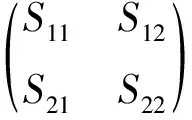
else

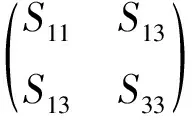
4 数值模拟

本部分中，我们给出数值例子来评估新算法的性能.我们首先根据图1、图2和图3产生数据作为训练样本，生成两类具有不同维度和样本大小的数据.然后，我们使用训练样本作为测试样本并利用通过新算法得到的协方差矩阵进行两总体的判别分析.最后，将误判率与利用(5)式定义的传统样本协方差矩阵进行判别分析[11]作比较，仿真结果如表1所示.

图1 15维数据网络

图2 50维数据网络

图3 80维数据网络

表1 不同样本量和维数下传统方法与新方法的误判率

通过表1可以看出，在数据维数p大于样本量n的情况下，由于传统方法估计的协方差矩阵是不可逆的，所以无法进行判别分析.而我们用新方法估计的样本协方差矩阵在“大p小n”的情况下是可逆的，所以可以进行判别分析，并且由表1的数据我们可以看出，新方法的误判率几乎为0，即判别效果良好.

5 结 论