翻折视角下的全国卷立体几何试题

广东省佛山市教育局教研室(528000) 彭海燕

全国卷高考立体几何重视考查几何元素间位置关系、度量关系,重视考查空间向量解决几何问题这一重要工具.回顾和审视全国卷历年试题的命制,我们发现有一条清晰的脉络,那就是特别重视基本平面几何图形性质的空间探索,也即特别重视四边形翻折前后的几何元素关系、度量关系的变与不变的考查.这样命题有助于充分考查考生的空间想象能力,有助于从熟悉的四边形要素的位置关系进入到空间几何体的几何要素关系的把握上.

1.筝形翻折

筝形是指有一条对角线所在直线为对称轴的四边形,与菱形定义相对应.菱形是特殊的筝形.筝形的一条对角线所在的直线垂直平分另一条对角线.

在筝形平面到空间变换的研究中,常常沿着其中一条对角线进行翻折.在翻折过程中,两条对角线垂直关系保持不变,这就成为高考试题命制的基础,常常利用两个对应的等腰三角形来描述空间筝形.这样的高考试题极为丰富.

例1-1 (2017年高考全国卷III 文科第19 题)如图1,四面体ABCD中,是△ABC正三角形,AD=CD.

(1)证明：直线AC⊥BD;

(2)已知ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.

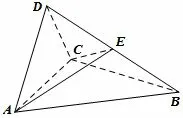
图1

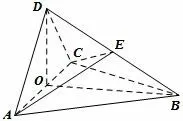
图2

锥体视角本题学生一般都会将其视作是四面体,并且需要通过几何元素位置关系和数量关系来描述四个面的三角形特征—等腰三角形(一个等腰直角三角形ADC、一个等边三角形ABC、两个全等的等腰三角形DBA,DBC),第一问的异面直线垂直的解决可以利用两个等腰三角形三线合一进行处理,再通过简单的解三角形运算得到点E为BD中点,进而得到两个四面体体积比为1.

筝形翻折视角如果我们从筝形ABCD的视角来看,沿着对角线AC翻折,对角线BD始终垂直AC,△ADC翻折的第一个位置即是平面DAC⊥平面ACB(∠DOB=90°),此时有AB=BD=BC=第二个位置根据题设其实就是要保持△ADC不变形,也即△ADC ～=△AEC,这样的点只可能是线段BD中点(Rt△BOD中∠DBO=30°),如图2所示,此时∠DOE=60°,△AEC为等边三角形.

从翻折的视角来看,整个问题的方向是非常清晰的,更能把握问题的本质.

其实,高考全国卷一直都重视筝(菱)形翻折问题的研究,并且有延续性,强调其稳定.近期的考题还有：

例1-2 (2013年新课标卷I 文科)如图3,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.证明：AB⊥A1C.

图3

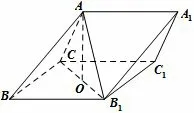
图4

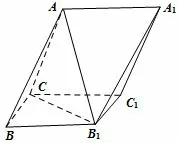
图5

例1-3 (2014年新课标卷I 文科)如图4,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.

(1)证明：B1C⊥AB;(2)略.

例1-4 (2014年新课标卷I 理科)如图5,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.

(1)证明：AC=AB1;(2)略.

上述三题学生在解决的时候,往往将其看作是不同的问题(三棱柱形态不一样),但是从翻折的视角来看,本质一样,要研究的都是筝形的翻折(图3是筝形CAA1B,图4,图5是筝形BB1AC,2014年理科试题要证明其为筝形,是文科试题的逆向探讨),显然例1-1 是上述试题的延续.这告诉我们高考命题具有较强的稳定性(哪怕外在形态多变,本质要求不变).延续这一做法的还有2015年全国卷I 理科第18 题的筝形翻折和2016年全国卷II 卷的菱形翻折.

对于筝形的研究,回归到教材(人教A2007年2月第三版)会让我们对“教材是一个训练系统,是一个基本模型发源地”有着更为清晰的认识,事实上,教材在练习习题与复习参考中多处多角度对筝形模型进行了探讨,上述考题不过是教材问题的延伸,图形结构一致,处理方法也一致,本质不变.

例1-5 (必修二第67 页练习第1 题)如图6,三棱锥V-ABC中,V A=V C,BA=BC.求证：V B⊥AC.(类似地,习题2.3 中A 组题4,B 组题2 都是这一问题的探索).

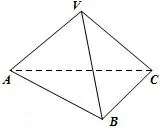
图6

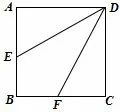
图7

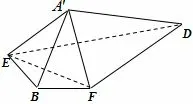
图8

例1-6 (必修二第79 题复习参考题第1 题)边长为2 的正方形ABCD中,如图7,点E是AB的中点,点F是BC的中点,将△AED.△DCF分别沿DE.DF折起,使A.C两点重合于点A′,如图8,连接EF,求证：A′D⊥EF.(类似地,P69 练习也是这一问题的探索).

对于教材中的这些练习、习题、复习参考题关键是要能系统地从图形结构出发,引导学生观察发现图形的基本结构特征,并能将其上升到筝形这一基本模型上来,把握筝形翻折前后的几何元素的位置关系,度量关系,总结证明的基本套路,即分别从两个公共底边等腰三角形中寻找线线垂直进行得到线面垂直,再到异面直线垂直等等.在模型探究、思想方法总结提炼的基础上落实直观想象与逻辑推理核心素养.

2.梯形的翻折

梯形是学生较为熟悉的平面四边形,虽然初中阶段对梯形的性质研究依然弱化,但在高中阶段,其仍然是重要的平面四边形(当然也可以从图形拼接的角度来看待梯形),梯形中,等腰梯形和直角梯形是重要的研究对象.

2.1 等腰梯形的翻折

等腰梯形的翻折主要强调对腰的翻折,也即保持底面的矩形特征,两腰向中间翻折,而这里面就有两底的端点是否合拢的问题.近两年的高考试题分别研究了上述问题.

例2-1 (2016年全国卷I理科)如图9,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.

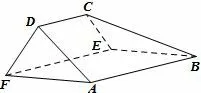
图9

(1)证明：平面ABEF⊥平面EFDC;

(2)求二面角E-BC-A的余弦值.

空间多面体视角本题学生会根据题设条件将图形直接视作是多面体,并利用底面正方形和侧面三角形为直角三角形的数量特征来解决第一问.但第二问对于大部分学生来说,由于缺乏对二面角作为条件时,本质是聚焦二面角概念这一常见命题规律的把握,而采取空间向量法处理(当年的高考广东卷阅卷时发现第二问失分极为严重,抽样均分为5.29,基本上来自于第一问得分).

图10

梯形翻折视角如果我们将空间几何体两面AFD,BEC放平的话,本题便可以视作是由一个等腰梯形翻折而成(高考试题分析对此探讨了命制过程).如图10,这是一个下底为上底两倍,高与上底相等的等腰梯形.也即CD=2AB,AF=AB,且AF=2FD.分别沿着两个高AF,BE将两条腰进行等速翻折,在翻折过程中,AF⊥DF,AF⊥EF关系始终保持不变,这也就保证了平面ABEF⊥平面EFDC这一关系始终不变.在此过程中二面角D-AF-E与二面角C-BE-F始终相等且分别是等腰梯形CDFE的下底角.题目翻折的位置是这个底角为60°的时候.在翻折过程中研究二面角E-BC-A可以有多种方式,既可以构建空间直角坐标系,也可以直接利用翻折过程中的对称性,结合直角三角形(无论如何翻折E到BC的高或者F到AD的高始终不变,且是构成二面角平面角的一个边)等积法求得相关的边长获得空间角的正弦或者余弦值.一个自然想法是,在翻折过程中必然会有C,D重合的时候,此时便构成了一个四棱锥,而这恰恰就是2017年立体几何文理科试题的命题背景.

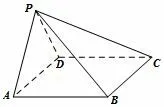
图11

例2-2 (2017年全国卷I理科第18 题)如图11,在四棱锥P-ABCD中,AB//CD,且∠BAP=∠CDP=90°.

(1)证明：平面PAB⊥平面PAD;

(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.

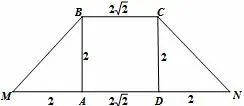
图12

梯形翻折视角如上可知,命题组在命题时必然考虑过等腰梯形底顶点重合的问题,本题即是如此.如图12,根据题设的位置关系和数量关系,我们将其视作是一个下底为上底为高为2 的等腰梯形.沿着高分别翻折,使得M,N重合,也即得到点P,此即为本题的命题背景.第一问的设计是自然而言的事情,也是2016年高考题的延续,因为无论怎样翻折两个面的垂直是一定的.第二问也是2016年高考题的延续.如果在复习中从翻折的视角来看待,2017年的高考题不过是2016年高考的翻版.

2.2 直角梯形的翻折

如图所示,在直角梯形中有一类由两个直角三角形,特别地,其中一个是等腰直角,拼接而成的直角梯形是翻折问题考查的热点.

这类翻折问题,一般都沿着两个三角形公共边AC进行翻折,如图13,翻折的位置往往强调两个面互相垂直,这样容易考察线面垂直和面面垂直中的性质定理与判定定理.具体操作时要注意翻折前后的点与线、线与线位置关系变与不变.数量关系的变与不变.

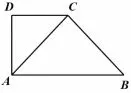
图13

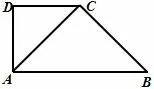
图14

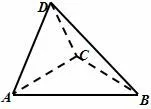
图15

例2-3 (2009年佛山二模)如图14,在直角梯形ABCD中,∠ADC=90°,AB//CD,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图15所示.

(I)求证：BC⊥平面ACD;

(II)求几何体D-ABC的体积.

本题是直接从平面图形进行切入进行翻折,笔者在命制的时候考虑到学生会如何考虑等腰直角三角形,一方面可以从等腰三角形ADC底边AC三线合一角度来思考,一方面也可以直接从等腰三角形ACB的直角边BC边来思考,不同方向涉及到的定理前后顺序不一致,解题长度不一致.目的是熟悉三角形的性质和空间的垂直(判定、性质)定理.这样的题目也较为常见,但基本上落脚点就是三角形的几何性质.

3.矩形(正方形)的翻折

矩形是大家比较熟悉平面图形,对于矩形的翻折问题,常常聚焦于具有一定长宽比的矩形翻折问题.如图16.

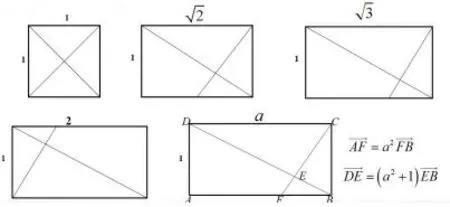
图16

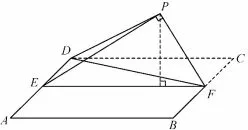
图17

在这些图形中,矩形一条对角线垂直于另外一边与所对顶角,并且都有相应的比例关系.类比于筝形,在图形沿着对角线BD或者CF翻折过程中,垂直关系始终保持不变,而这个就是命题的落脚点.笔者近两年对这类问题进行了探索,全国卷2018年考题也进行了正方形的翻折研究.

例3-1 (2018年全国卷I理科第18 题)如图17,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.

(1)证明：平面PEF⊥平面ABFD;

(2)求DP与平面ABFD所成角的正弦值.

相比较于前几年的全国卷命题中的隐性翻折,本题则直接从正方形ABCD沿一边重点翻起一个直角△DFC来,翻起来的位置从对称的角度来看,其实就是把直角△ABF翻起来,B,C重合的位置就是点P的位置.根据对称性,此时点P在底面射影H肯定在等腰△AFD中线EF上,至于平面PEF⊥平面ABFD是自然而言的事.至于第二问,不难用等积法算得而DP与平面ABFD所成角平面角PDH的正弦值

我们回到前面2016年和2017年的考题来看,本题只不过把原来的等腰梯形换成了正方形,仍然是从对称的两个方向进行翻折,让它们重合,成为一个三棱锥,如图18,我们从视角差异的角度,换个方向来看,翻折而成的这个三棱锥又是一个筝形,难道这是巧合吗? 回味上述全国卷这6年的考题,这次第18 题是否如《沙家浜》中阿庆嫂所说：“这茶,喝到这时,是不是才喝出点味儿来了! ”

作为高考卷命题的研究者和地区质量检测的命题者,结合高考题的这种命题特点,我们对矩形的翻折进行了多角度的探索,命制了多个考题.这里呈现出来,供读者朋友参考,以期对高考试题命制提供不同的探索方向,为素养导向的命题提供一些思考.

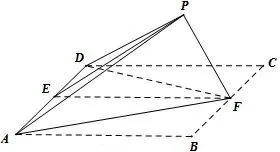
图18

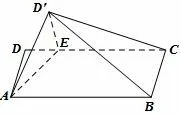
图19

例3-2 (2017年佛山二模文理科第19 题)如图19,矩形ABCD中,AB=4,AD=2,E在边DC上,且DE=1,将△ADE沿AE折到△AD′E的位置,使得平面AD′E⊥平面ABCE.

(I)求证：AE⊥BD′; (II)(理科)求二面角D′-AB-E的余弦值.(文科)求三棱锥A-BCD′的体积.

例3-3 (2014年佛山一模文理科第18 题)如图20,矩形ABCD中,AB=12,AD=6,E.F分别为CD.AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE位置(如图21 所示),连结AP,PF,其中

(I)求证：PF⊥平面ABED;

(II)(理科)求直线AP与平面PEF所成角的正弦值.(文科)在线段PA上是否存在点Q使得FQ//平面PBE?若存在,求出点Q的位置;若不存在,请说明理由.

(III)(文)求点A到平面PBE的距离.

图20

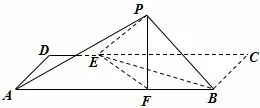
图21

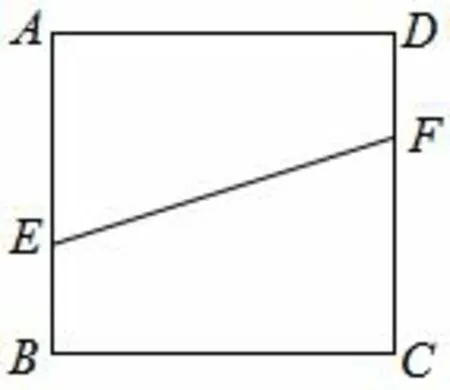
图22

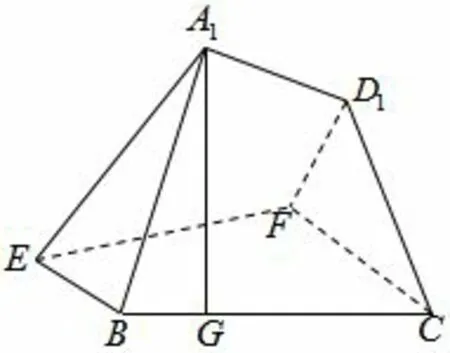
图23

本题的设计思路与例3-1 有许多相同之处,研究视角也很有趣.

例3-4 (2013年佛山二模理科第19 题)如图22,设正方形ABCD的边长为3,点E,F分别在AB,CD上,并且满足AE=2EB,CF=2FD.如图23,将直角梯形AEFD沿EF折到A1EFD1的位置,使点A1在平面EBCF上的射影G恰好在BC上.

(I)证明：A1E//平面CD1F;

(II)求平面BEFC与平面A1EFD1所成二面角的余弦值.