基于符号计算的BBM方程的精确解

胡凯丽，李 岩

(陕西师范大学 计算机科学学院，陕西 西安 710119)

0 引 言

随着计算机科学的迅猛发展，计算机技术越来越多地服务于各行各业，如教育、医疗、交通等。在数学领域，也逐渐兴起了与计算机相结合的学科，即计算机代数。20世纪60年代早期，诞生了最早的计算机代数系统，科学家用LISP语言编写了第一个符号积分程序，随后一些专业化计算机代数程序也开始问世。计算机代数也被称为符号代数计算(简称符号计算)，是数学、计算机科学和人工智能等领域新兴的交叉学科。

在不断探索和解决各种复杂问题的过程中，人们发现非线性这一现象普遍存在于自然界、人类社会等众多领域。20世纪60年代以来，研究非线性现象获得了巨大的进展，其应用也变得较为广泛，由此发展形成了研究非线性现象的普遍规律学科，即非线性动力学。随着科学技术的不断发展，非线性动力学已经广泛地渗透到了各个领域，例如通信技术、计算机技术、材料科学、生命科学、动力系统等。因此，非线性偏微分方程的求解问题成为了研究的重点。近年来，人们提出了多种求解非线性偏微分方程的方法，例如齐次平衡法[1]、Tanh函数展开法[2-4]、Hirota双线性展开法[5]、Jacobi椭圆函数展开法[6]、(G'/G)-展开法[7]等。文献[8]提出了推广的(G'/G)-展开法—(G'/G2)-展开法，实践表明，(G'/G2)-展开法在求解非线性微分方程时具有简单、快捷等优势，已求解了部分方程[9-16]。因此，文中利用该方法研究Benjamin-Bona-Mahony[17-19]方程。

文中应用符号计算系统Maple并借助PDEtools工具包，结合(G'/G2)-展开法求解BBM方程，当精确解中的常数取特殊值时得到方程的孤波解，利用plots工具包绘制出孤波解的三维图。

1 (G'/G2)-展开法

考虑如下形式的非线性偏微分方程：

P(u,ux,ut,uxx,uxt,utt,…)=0

(1)

其中，u=u(x,t)是未知函数，P是关于u及u的各阶偏导数的多项式。利用(G'/G2)-展开法求解方程1的具体步骤如下：

第1步：对方程1作行波变换u=u(ξ),ξ=x-Vt,得到如下常微分方程。

Q(u,u',u'',u''',…)=0

(2)

第2步：假设方程2有如下形式的解。

(3)

其中,G=G(ξ)且满足二阶线性常微分方程。

(4)

其中，αi,a,b是待定常数；m可以通过齐次平衡法得到。

利用Maple求解方程4的具体过程如下所述：

(1)调用Maple的PDEtools工具包，输入方程4；

(2)利用dsolve()方法直接求解方程4，得到G(ξ)的值；

具体代码如下：

>restart：with(PDEtools)：

>eq1:=diff(diff(G(xi),xi)/G(xi)^2,xi)=a+b*(diff(G(xi),xi)/G(xi)^2)^2;

>eq2:=psi(xi)=diff(G(xi),xi)/G(xi)^2;

>eq3:=dsolve(eq1,G(xi));

>eq4:=dsubs(eq3,eq2);

由上述过程，方程4有以下三组解：

(1)当ab>0时

(5)

(2)当ab<0时

(6)

(3)当a=0，b≠0时

(7)

其中，C1,C2为任意常数。

第3步：将式3代入方程2，借助方程4，可以得到关于(G'/G2)的多项式，令其各次幂的系数为零，可得到一组关于αi,a,b的代数方程组，通过求解方程组得到αi,a,b的值。

第4步：将第3步得到的结果代入方程3和方程4，即可得方程1的解。

2 (G'/G2)-展开法的应用及实现

根据第1节中的算法步骤，借助Maple，现考虑如下形式的BBM方程。

ut+ux+uux-uxxt=0

(8)

将行波变换u(x,t)=u(ξ),ξ=x-Vt代入式8，然后对其两边积分，取积分常数为零，得到：

-Vu+u+(1/2)u2+Vu''=0

(9)

由齐次平衡法得N=2。因此，设方程8的解为：

(10)

利用式4和式10，分别求出u'',u2的值，将u'',u2的值代入式9，得到：

(11)

令(G'/G2)的各次幂系数分别为零，可以得到以下两组参数：

(12)

(13)

Maple符号计算代码如下：

>PDEeq:=diff(u(x,t),t)+diff(u(x,t),x)+u(x,t)*diff(u(x,t),x)-diff(u(x,t),x,x,t);

>ode1:=dsubs(u(x,t)=u(x-V*t),PDEeq);

>ode2:=subs(x-V*t=xi,ode1);

>ode2:=convet(ode2,diff);

>ode3:=int(ode2,xi);

>ode4:=dsubs(u(xi)=alpha[0]+alpha[1]*psi(xi)+alpha[2]*psi(xi)^2,ode3);

>ode5:=dsubs(diff(psi(xi),xi),ode4);

>ode6:=collect(ode5,psi);

>ltt:=[ ]：

for i from 1 to nops(ode6)

do p(i):=coeffs(coeffs(op(i,ode6)),psi(xi))；

ltt:=[p(i),op(ltt)]；

end do:

ltt;

>solve(ltt,{alpha[0],alpha[1],alpha[2],V});

则方程8的解为：

(14)

(15)

把方程4的解即(G'/G2)的值分别代入式14和式15,可得BBM方程的精确解。

第一种情况，将方程4的解代入式14：

(1)当ab>0时，得到的三角函数通解为

(16)

(2)当ab<0时，得到的双曲函数通解为：

(17)

对于式17，考虑以下两种特殊情况，可获得如下形式的孤立波解：

(a)当C1≠0,C2=0时，其孤立波解为:

(18)

若将式18中的常数分别取值为：a=0.5,b=0.9,V=1，利用Maple中的plots工具包可绘制出孤波解的三维图，如图1所示。

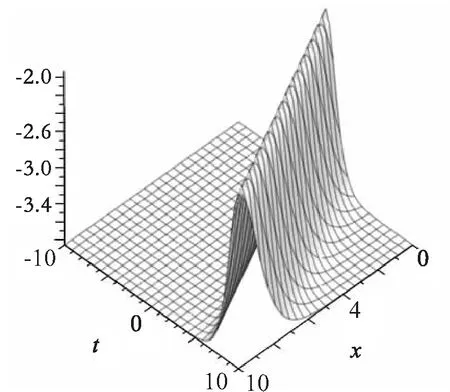
图1 孤波解的三维图(x=0…10,

(b)当C1=0,C2≠0时，其孤立波解为：

(19)

(3)当a=0,b≠0时，得到有理函数解为：

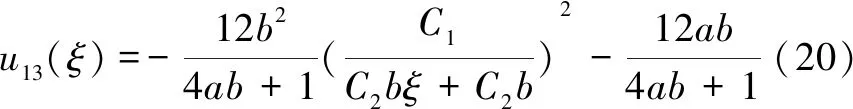
第二种情况，将方程4的解代入式15：

(1)当ab>0时，得到三角函数通解为：

(21)

(2)当ab<0时，得到的双曲函数通解为：

(22)

对于式22，考虑以下两种特殊情况，可获得其如下形式的孤立波解。

(a)当C1≠0,C2=0时，其孤立波解为:

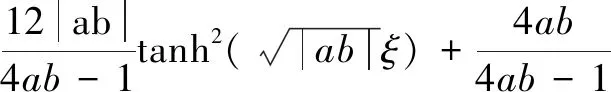
(23)

若将式23的常数分别取值为：a=2,b=3.7,V=0.21，利用Maple中的plots工具包可绘制出孤波解的三维图，如图2所示。

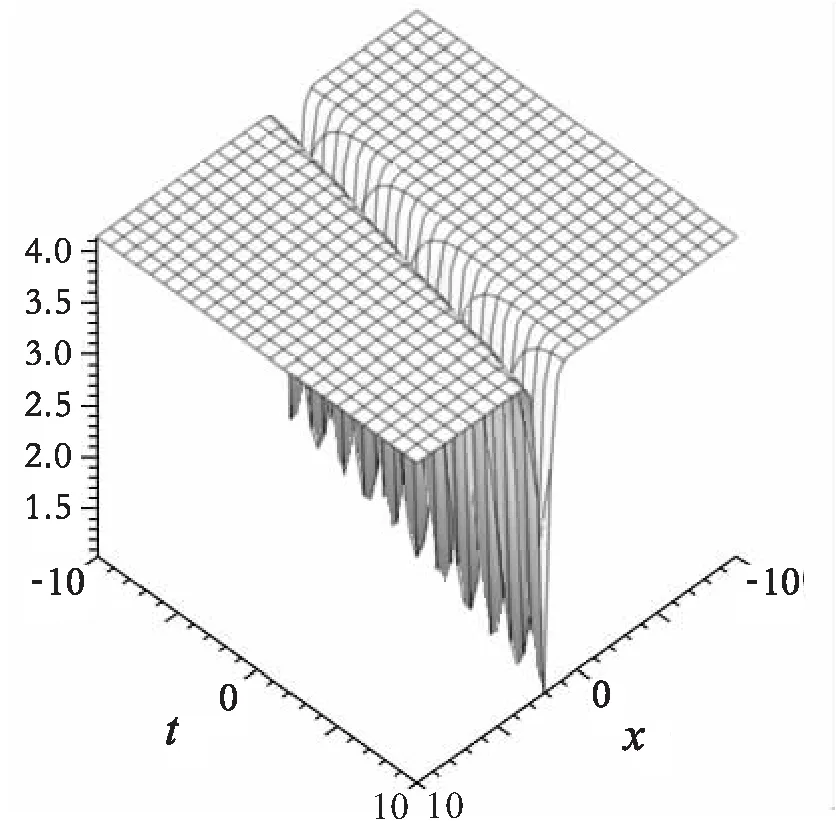
图2 孤波解的三维图(x=-10…10,

(b)当C1=0,C2≠0时，其孤立波解为：

(24)

(3)当a=0,b≠0时，得到的有理函数解为:

(25)

3 结束语

采用(G'/G2)-展开法研究了BBM方程，在符号计算系统Maple的帮助下，得到了方程的三角函数、双曲函数以及有理函数形式的精确解，且当双曲函数解中部分参数取特殊值时，得到了方程的孤立波解，从而丰富了BBM方程的精确解系。从求解过程及求得的精确解来看，该方法简单、高效，是求解非线性方程的较好选择。