在思考中学会思考

江苏 南二七

我们经常会困惑，为什么老师在解决问题时往往如行云流水一样自然，到了自己就变得磕磕绊绊、步履维艰；为什么身边的同学在解题时总会有一些奇思妙想、有如神助，而我们却总感力不从心.要说我们不会思考吧，数学中常用的思考方法我们也能头头是道说上若干，比如观察法、归纳法、逆向法、演绎法等等，可是一旦用它们“上阵杀敌”，却又觉得“无用武之地”.

实际上这是一种假象，一种心理作用.数学的思考确实有很多规律可循，基本方法也有很多，但是我们该怎样做才能牵住数学思考的“鼻子”，让这些规律、方法为己所用呢？今天就让我们一起在问题的思考中学习如何思考吧.

一、打铁先要自身硬

其实如何解题，如何思考，这项研究由来已久.目前最受推崇的做法是来自美国的数学家波利亚，其经典的做法是当我们拿到一个问题，常问自己以下几个问题：

“已知是什么？”

“要证（求）什么？”

“见过类似的问题吗？”

“可否将问题换一种说法？”

……

我们通常使用这些问题来启发自己寻找到解题的思路.可能有些同学也曾做过类似的尝试，不过效果却因人而异，因时而异.有时这样做成功了，有时却一筹莫展，有时别人成功了，能看到我们看不到的条件，想到我们想不到的方法.这时好时坏的，问题的关键在哪里呢？

实际上，要想取得好的效果，我们就必须在平时的练习中做好积累工作，尽可能地将问题归类，并将解决问题的方法用图式进行整理记忆，形成固定的基本模式.这就是我所指的“硬功夫”.当我们遇到一个问题时，如果我们已经有了解决问题的这个图式，就会有很大的成功率，那么这是一个怎样的图式？又怎样才能形成这样的图式？我们来看以下做法.

例1求函数f（x）=x2-2ax-1在区间[1，3]上的最小值.

此题对同学们来说不算太难，这是因为我们已经在头脑中形成了一个图式，即依据对称轴与区间的位置关系，可分三种情况进行讨论求解.

解二次函数开口向上，对称轴x=a.

（1）当a ≤1时，函数f（x）在区间[1，3]上为单调递增函数，所以f（x）min=f（1）=-2a；

（2）当a ≥3时，函数f（x）在区间[1，3]上为单调递减函数，所以f（x）min=f（3）=8-6a；

（3）当1＜a＜3时，函数f（x）在区间[1，3]上先减再增，所以f（x）min=f（a）=-1-a2.

变式1求函数f（x）=x2-2x-1在区间[a，3a-2]上的最大值.

如果再用上述方法解决这一问题就会遇到大麻烦了.事实上，画出图形，发现图象开口向上，则区间端点谁离对称轴远谁的函数值就大，因此要根据区间的中点分为两种情况讨论.

解二次函数开口向上，对称轴x=1.

可见我们一开始认识的图式并不是计算二次函数最值的图式，而只是计算开口向上的二次函数的最小值的一个图式.而且，上述问题还只是开口向上的一类，开口向下的二次函数又怎么办？这就需要我们将此问题归类，通过练习不断积累，最后形成如下的图式，从而利用这一图式来解决二次函数的最值问题.

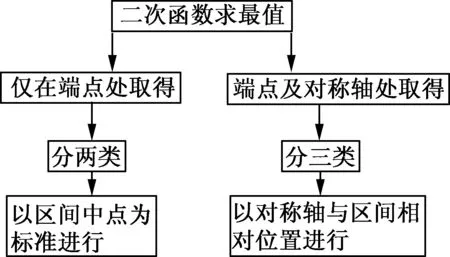
变式2已知函数f（x）=ax2+（2a-1）x+1在区间上的最大值为1，求实数a的值.

若按常规想法进行分类讨论，太麻烦了，比如.

①a=0吗？

②a≠0时函数图象的开口方向呢？

③对称轴与区间的位置关系如何？

④当对称轴在区间内时，对称轴与区间端点的距离不明，如此就要分很多种情况进行讨论.

实际上，按照我们形成的图式所指，其最值只会在端点和对称轴处取得，因此有如下解法.

解当a≠0时，因为函数的最大值只会在处取得，则

a=0时，显然不符合题意.

有了这种图式在解题思考中作为思考的平台，就好像站在巨人的肩膀上，自然比别人看得远，想得深.如果我们平时的学习中能够形成若干个这样的图式，相信一定会对解题起到巨大的作用，而这一工作从高一就开始做最好，长此以往，到高三之后，同学们一定会成为解题的高手.

二、广交朋友千里行

俗话说，“一个篱笆三个桩，一个好汉三个帮”.同学们，不要以为我们在解题时一直是孤军奋战的，实际上我们有很多好朋友在等待着提供帮助.在此我要给大家隆重介绍两个重要的帮助思考的朋友，它们是“图象”和“特殊化”.当我们在解题遇到困难时，一定不要忘记呼唤它们来协助我们战胜困难.除了自身强大，一身“硬功夫”，再有个好人缘，解题想不顺利都难.

变式3若不等式x2-2ax+1≤0在区间[1，3]上恒成立，求实数a的取值范围.

一般的，可以设函数f（x）=x2-2ax+1，所以不等式x2-2ax+1≤0在区间[1，3]上恒成立即函数f（x）在此区间的最大值f（x）max≤0，从而问题转化为求函数f（x）的最大值.

但是，更为简单的做法是通过分离变量再利用图象求解.

解不等式x2-2ax+1≤0等价于x2+1≤2ax，即又可以作出函数在区间[1，3]上的图象，可知g（x）max=g（3）=即

变式4若不等式x2-2ax+2＞a在区间[-1，+∞）上恒成立，求实数a的取值范围.

解法1即x2-2ax+2-a＞0，考查函数f（x）=x2-2ax+2-a的图象，如图1、图2两种情况，

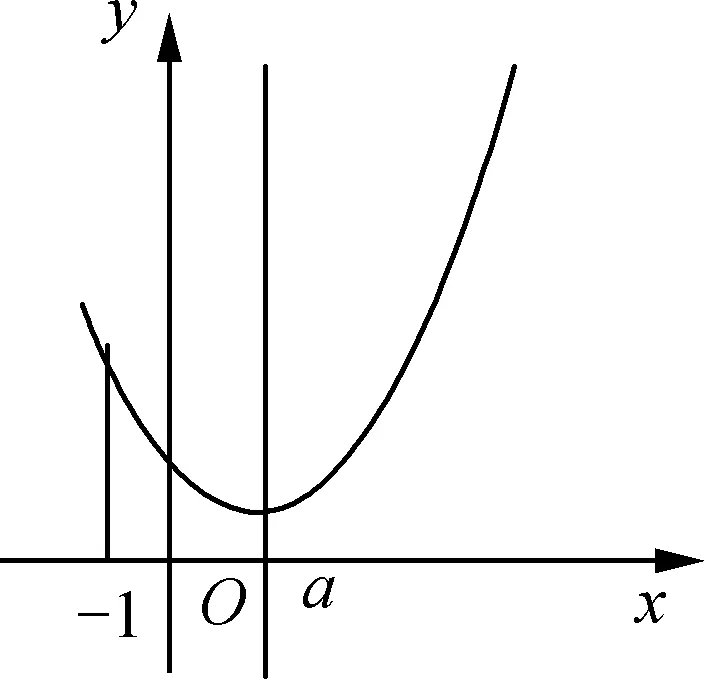
图1

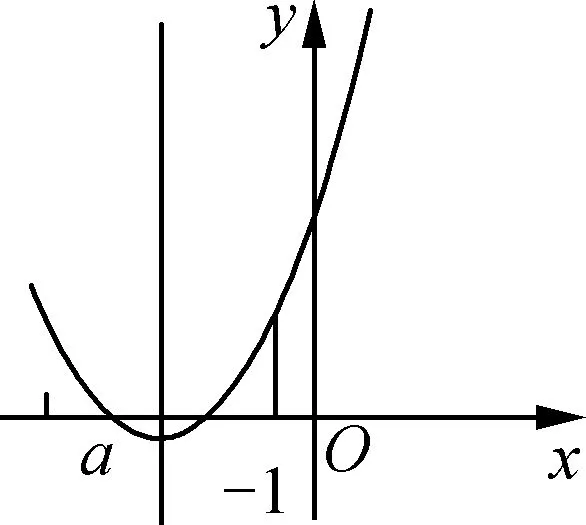
图2

不等式成立的条件是：

①Δ＜0时满足，解得a∈（-2，1）；

综上，a∈（-3，1）.

解法2由x2-2ax+2-a＞0可得x2+2＞2ax+a=a（2x+1），在坐标系内分别作出两个函数y1=x2+2与y2=a（2x+1）的图象，而满足题意的直线l位于直线l1，l2之间，而直线l1，l2对应的a值分别为1，-3，如图3.可得a∈（-3，1）.

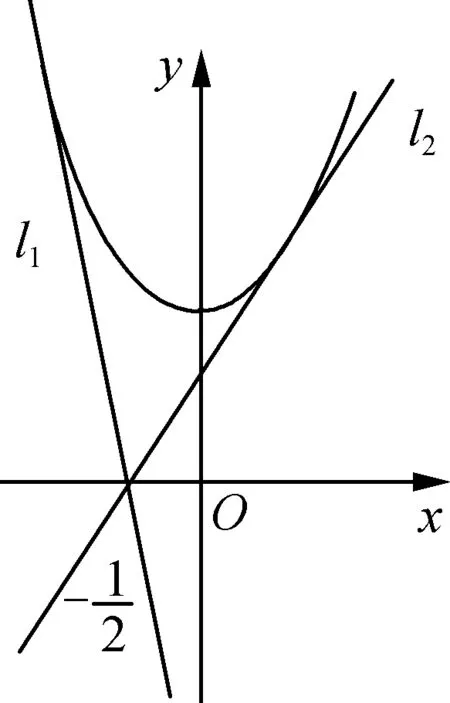
图3

可见利用数形结合可以让解题变得直观形象，多了几分“灵气”.因为运用数形结合解题往往能直接揭示问题的本质，正如我国著名数学家华罗庚先生所说：“数缺形时少直观，形缺数时难入微.”

相比数形结合，特殊化也是我们解题时的一盏阿拉丁神灯，有着巨大的作用.数学大师希尔伯特曾说过，“在讨论数学问题时，我相信特殊化比一般化起着更为重要的作用，这种方法是克服数学困难的最重要的杠杆之一.”

例2若函数f（x）的图象可由函数y=lg（x+1）的图象绕着原点O 逆时针旋转得到，则函数f（x）的解析式为 （ ）

A.10-x-1 B.10x-1

解从函数y=lg（x+1）的图象上任取一点A 如（9，1），将OA 绕着原点O 逆时针旋转得到点B（-1，9），分别代入各解析式，可得仅A合适，故选A.

同学们，通过以上的学习和思考，相信你对数学有了更为透彻的认识，也有了更系统、科学的方法，那么让我们从现在开始，不断尝试、不断积累，争做一个敢思考、会思考、乐思考的达人吧！