证据推理，数学课堂教学的应然追求

江苏海门市通源小学 曹晓丹

所谓“证据推理”，是指根据数学概念、法则、规律以及相关事实性知识，通过比较分析、抽象概括、归纳演绎等形成的一种推理。在小学数学教学中，学生的证据推理通常包括两个方面，一方面是根据证据经过推理得出科学结论，这是一种直接推理。另一方面是运用证据证实或证伪推理。证据推理，对培养学生直觉思维力、逻辑思维力，培育学生科学严谨的精神都具有重要作用。证据推理，是小学数学课堂教学的应然追求。

一、知识“结构化”，延伸“证据推理”广度

证据推理是一种“有根有据”的推理。当下，教师已开始重视学生合情推理能力的培养，但却有忽视学生演绎推理的迹象。由于合情推理的不确定性，因而深受师生欢迎；演绎推理具有确定性特质，往往需严密论证，因此很多学生漠视演绎推理。诚然，合情推理在学生数学学习中具有重要作用，但任何好的东西一旦变成形式，就可能变成坏的。例如，学生可能无由头猜想，甚至乱猜、瞎猜，由此造成学生数学学习随意性的倾向，他们往往是跟着感觉走，从而虚化了数学思维的严谨性。真正有意义、有价值的数学猜想应当是学生逻辑思维的压缩、简化，是略去中间烦琐的证明环节，是直观的、跳跃性的。从这个意义上说，合情推理也应是一种证据推理。

为了拓宽学生推理的广度，教师必须引导学生将数学知识结构化。结构化知识犹如一个“带钩的原子”，储存在学生头脑中，便于学生提取、调用、推理。很多学生，之所以不善于进行证据推理，就是因为知识在学生头脑中没有形成一种结构，知识由此失去应有的“活性”。知识结构化不仅表征了知识的本质，而且还表征了知识点之间的关联。例如，在教学“圆柱的体积”时，学生在动手操作的实验过程中，将圆柱体切拼成长方体，由于不同的摆放位置，而形成不同的底面和高。学生根据操作直观认为圆柱的体积等于底面积乘以高，也等于侧面积一半乘以半径，还等于高与半径的乘积再乘以圆柱底面周长的一半。这是一种合情推理，是学生建立于操作感知基础上的合情推理。那么，如何运用已有数学知识进行证明呢？学生主动调用五年级的“圆的面积”知识以及六年级的“圆柱侧面积”等相关知识演绎证明。最后，学生发现，尽管圆柱体积表征形式不同，但都可以转化成半径和高相乘的形式，即V=πr2h。在这个过程中，学生不仅通过操作直观，而且借助已有知识，从数学学理上严密证明了圆柱体积公式内在的一致性。

证据推理能力是学生数学核心素养的重要组成部分，它既需教师潜移默化的引导、渗透，更需学生用孜孜以求的精神去领悟、践行。教学中，教师要丰富学生数学知识，尤其是要让学生掌握数学概念的内涵和外延，洞察数学知识本质，只有这样，才能开掘、丰厚学生的数学推理能力，夯实学生数学推理根基。

二、学习“逻辑化”，强化“证据推理”角度

学生数学学习过程应当是一个逻辑化过程。所谓“逻辑化”，是指学生根据自己已有知识经验，在条件和问题之间建立某种符合逻辑的连结，从而发现、认识数学未知知识的过程。作为教师，要站在学生立场，设计出符合学生思维品质、想象特质和认知规律的学习过程。每一个学生，由于其解决问题的思路不同，因而证据推理过程也可能不同，但不同的证据推理，其推理的逻辑性却是一以贯之的，尊重学生推理产生的差异，就是要强化学生推理角度。

例如，在教学“多边形内角和”时，笔者先放手让学生探究，于是，绝大部分学生都按照探究三角形内角和的方法，用“量一量”“拼一拼”等方法对四边形进行数学实验。当学生操作探究到五边形时发现，五边形的所有内角拼成的不是周角，因而只能通过测量法进行测量。而测量法误差较大，于是学生想到是否可以借助三角形内角和来探究。以小组为单位，学生对多边形内角和进行探究。学生在小组汇报交流中，形成了两种不同的推理模式。以六边形为例，如图1、图2：

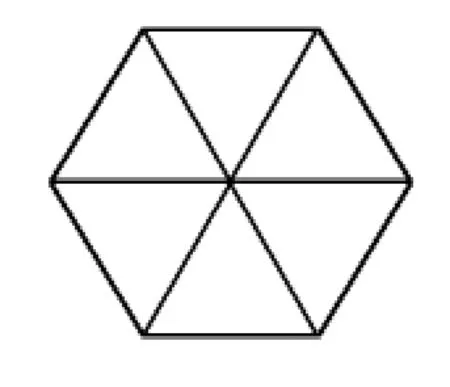
图2

图1的推理模式如下：因为六边形可以分成四个三角形，又因为每一个三角形的内角和都是180°，所以六边形的内角和就是180°×4。图2的推理模式如下：因为六边形可以分成六个三角形，又因为每个三角形的内角和都是180°，因此，六个三角形的内角和就是180°×6，同时因为六个三角形中间形成的周角不属于六边形原来的内角，因此要用6个180°减去2个180°，也就是4个180°。

在小组交流汇报的基础上，笔者将多边形内角和用表格整理出来，帮助学生发现“多边形边数与多边形内角和之间的关系”。学生认为，n边形内角和等于（n-2）个三角形的内角和。这是学生依据四边形、五边形、六边形等多边形作出的一种不完全归纳推理，这种推理的依据是基于学生对规律的认知。那么如何从学理上严格证明呢？学生展开深度思考。通过观察多边形的边，有学生这样推理：任何一个多边形从一点出发都可与对边构成三角形，与邻边不能构成三角形，所以n边形的内角和等于（n-2）个三角形的内角和；还有学生这样推理：任何一个多边形都可以从中心点出发，将多边形分成个数与边数相等的三角形，又因为中心点处形成的周角不属于原来多边形内角，所以n边形的内角和等于（n-2）个三角形内角和。

不同的学生，其思维有着不同的条理性。作为教师，要允许、鼓励学生选用不同论证方式，从不同视角进行推理。通过展示学生有根据的逻辑推理，帮助学生突破学习难点。当学生经历了证据推理全过程，其推理、思维和认知能力必将得到提升。

三、探究“层次化”，拓展“证据推理”深度

数学推理既要重视整体的宏观求证，也要重视局部的微观求证；既要引导学生进行直接推理，也要引导学生进行间接证明；既要引导学生“证实”，也要引导学生“证伪”。学生搜寻证据的种类以及证明方式的不同，反映学生运用证据推理的深度不同。数学推理，就其形态而言，是动态的，包含了数学知识生长的过程。在证据推理过程中，有许多微小细节，这些细节却有着十分丰富的思想内涵，具有较大的思维价值。探究层次化，就是要拓展学生证据推理的深度。

例如，在教学“3的倍数的特征”时，笔者分层次教学，让学生的证据推理逐步深入。一开始，学生根据“2的倍数的特征”“5的倍数的特征”类比推理出“3的倍数的特征”。当学生通过举例验证发现“个位上是3的倍数的数不一定是3的倍数”时，学生会经历一个自我否定的过程，这是第一层次的类比推理教学。

在此基础上，笔者给学生提供一张百数表，让学生用探究2和5的倍数的特征的方法进行探究，回归学生的经验本源。当学生圈出3的倍数后，发现3的倍数不同于2和5的倍数，2和5的倍数都在同一列，3的倍数排成了“斜行”。并且发现，在同一斜行，3的倍数十位上依次加1，个位上依次减1。于是，笔者启发学生：什么保持不变？有学生很快想到一个数中两个数字的和保持不变。由此，学生形成合情推理：各个数位上数字的和是3的倍数，这个数就是3的倍数。学生通过举例，不完全归纳出“3的倍数的特征”，这是第二层次的不完全归纳推理教学。

继续深入，笔者引导学生从数的组成视角进行证据推理，以四位数为例，假设四位数是1000×a+100b+10c+d，1000×a+100b+10c+d=（999×a+99b+9c）+（a+b+c+d），因为“999×a+99b+9c”一定是3的倍数，所以只要“a+b+c+d”的和是3的倍数，这个数就是3的倍数。通过严谨的证据推理，学生不仅“知其然”，更“知其所以然”。

在上述教学中，第一层次类比推理，绝大部分学生都能想到，通过举例验证也能自然地自我否定；第二层次的不完全归纳，需要教师引导学生深入观察，同时恰当追问，引发学生形成猜想，通过举例进行不完全归纳；第三层次的证据推理，需要教师深入引导，促成学生深度理解、深刻感悟。

论证推理既需要学生建构结构化的数学概念，也需要教师鼓励学生进行逻辑化、层次化的探究。数学概念解决的是“推理证据”的广度问题，逻辑化学习过程体现的是“怎样推理”的角度问题，而层次化探究体现的是“推理得怎样”的深度问题。通过有广度、有角度、有深度的证据推理，能有效发展学生的数学“核心素养”。♪