有限域上斜λ-常循环码中互补对偶码的存在性及其性质
赵鹏程,李秀丽
(青岛科技大学数理学院,山东 青岛 266061)
代数编码理论,又称纠错码理论,是信息学的分支。该理论的发展源自现代通信技术和电子计算机技术中差错控制研究的需求,至上世纪七十年代末,纠错编码技术已经渗透到了众多领域[1]。随着科学的发展与实际需要,编码理论不断发展,应用范围日益扩大,作为线性码的一种特殊情况——常循环码,由于具有良好的代数结构和性质,人们进行了大量研究[2]。
目前,伴随着纠错码理论的发展,关于有限域上的λ-常循环码(λ-constacyclic codes)已经有了丰富的结论,同时数学家对有限域上的斜λ-常循环码(skewλ-constacyclic codes)进行了研究[3-8]。在普通多项式环的基础上,引入自同构映射,得到斜多项式环。自同构映射的加入使斜多项式环成为不可交换环,而其不可交换性使斜多项式环上的码字有了更大的讨论空间。斜λ-常循环码作为λ-常循环码的一种推广,受到了众多国内外学者的青睐,形成了编码理论在有限域和有限环上的新分支。
线性互补对偶码(linear complemetary-dual codes,LCD)具有良好的相关特性和正交特性,国内外学者在对常循环码中LCD码的存在性、构造、重量分布、最优码及其应用等方面做了大量的研究[9]。
本文主要研究了引入自同构映射后得到的斜λ-常循环码。在普通多项式环的基础上,引入自同构映射,得到新的多项式环,定义斜λ-常循环码。研究了斜λ-常循环码中互补对偶码在三种情况下的存在性,并且讨论了有限域上斜循环码中LCD码的计数问题。对于构造一些高效且纠错性能好的码和译码,具有一定的理论意义和应用价值。
1 基础知识
首先介绍一些基本概念[9-12]。
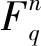
定义1.2设λ∈Fq,若对任意(c0,c1,c2,…,cn-1)∈C,有(λcn-1,c0,c1,c2,…,cn-2)∈C,称码C是一个λ-常循环码。特别地,λ=1时,称C是一个循环码。
定义1.3若一个循环码的所有码字多项式都是一个次数最低的非零首一多项式g(x)的倍式,即该码由g(x)生成,则称g(x)为该码的生成元或生成多项式。
定义1.4设C是q元域上的[n,k]线性码。其对偶码是C⊥,定义为:
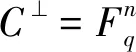
定义1.5设λ∈Fq,θ是Fq上的一个自同构映射,若对任意(c0,c1,c2,…,cn-1)∈C,有(λθ(cn-1),θ(c0),θ(c1),θ(c2),…,θ(cn-2))∈C,称码C是一个斜λ-常循环码。特别地,λ=1时,称C是一个斜循环码。
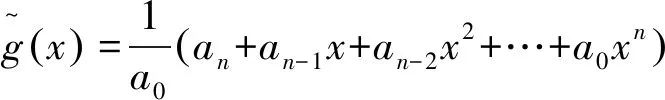
定义1.7引入Fq上自同构映射θ,定义一种新的运算“*”,满足axm*bxn=aθm(b)xm+n。
例如在有限域F22={x+yα|α2+α+1=0,x、y∈{0,1}}上,定义自同构映射θ:F22→F22,θ:ξ→ξ2。
则αx2*(1+α)x=αθ2(1+α)x3=α(1+α2+2α)2x3=x3。
2 有限域上斜λ-常循环码中的线性互补对偶码
定理2.1当λ=1时,如果Fq上[n,k]斜循环码C的生成多项式为g(x),则如下条件等价: (1)C是LCD码;(2)g(x)是自反的。
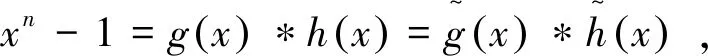
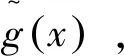
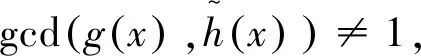
例2.1在有限域F22={x+yα|α2+α+1=0,x、y∈{0,1}}上,定义自同构映射θ:F22→F22,θ:ξ→ξ2。
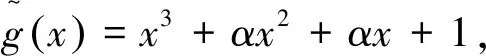
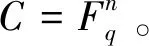
证明:假设C是Fq上长度为n的非零码,因为C既是斜α-常循环码又是斜β-常循环码,所以满足对任意
(c0,c1,c2,…,cn-1)∈C,
(αθ(cn-1),θ(c0),θ(c1),…,θ(cn-2))∈C,
(βθ(cn-1),θ(c0),θ(c1),…,θ(cn-2))∈C。
又因为C是线性码,所以
((α-β)θ(cn-1),θ(c0),θ(c1),…,θ(cn-2))∈C。
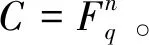
定理2.3假设C是一个斜λ-常循环码,并且长度为n,如果dim(C) dim(C∩C⊥)≤dim(C), 且 dim(C∩C⊥)≤dim(C⊥), 所以 dim(C∩C⊥) 从而 所以 C∩C⊥={0}, 即C是LCD码。 证明C∩C⊥既是斜λ-常循环码也是斜λ-1-常循环码。则根据定理2.2,C∩C⊥满足 C∩C⊥={0}, 或 C∩C⊥={0}, 从而C是LCD码。 定理3.1设n=2ps,p=5,q=pm(p为素数)。给定Fq上的自同构映射θ:α→α5。假设Fq={0,1,ξ,ξ2,…,ξq-2},ξ是xq-1=1的根,则有限域Fq上长度为n=2·5s的斜循环码中LCD码的个数为5s+1。 (x-δ)*(x-δ3)=x2-(δ3+δ)x+1,又δ4=1即δ2=±1,根据域上元素的不可重复性得出δ2=-1,所以δ3+δ=(δ2+1)δ=0,进而得到x2+1=(x-δ)*(x-δ3)。 显然(x-δ)和(x-δ3)在Fq[x]上形成一对互反多项式。 xn+1=(x2+1)5s=(x-δ)5s*(x-δ3)5s, 所以Fq上长度为n=2·5s的斜循环码中LCD码的个数为5s+1。 情况2:令q≡-1(mod4),则x2+1在Fq[x]上是不可约的并且是自反的, xn+1=(x2+1)5s, 所以Fq上长度为n=2·5s的斜循环码中LCD码的个数为5s+1。 定理3.2设n=3ps,p=7,q=pm(p为素数)。给定Fq上的自同构映射θ:α→α7。假设Fq={0,1,ξ,ξ2,…,ξq-2},ξ是xq-1=1的根。则有限域Fq上长度为n=3·7s的斜循环码中LCD码的个数为(7s+1)2。 (x-δ)*(x-δ3)*(x-δ5) =(x+1)*(x-δ)*(x-δ5) =x3-(θ2(δ5)+θ(δ)-1)x2+(θ(δ)θ(δ5)-θ(δ5)-δ)x+1 =x3+(δ2-δ+1)x2+(δ2-δ+1)x+1, 又因为δ3+1=(δ+1)(δ2-δ+1)=0,即(δ2-δ+1)=0。所以x3+1=(x+1)*(x-δ)*(x-δ5),(x+1)在Fq[x]上是自反的,并且显然(x-δ)和(x-δ5)在Fq[x]上是互反多项式。得到: xn+1=(x3+1)7s=(x+1)7s*(x-δ)7s*(x-δ5)7s, 所以Fq上长度为n=3·7s的斜循环码中LCD码的个数为(7s+1)2。 情况2:令q≠1(mod6)则x2-x+1在Fq[x]上不可约,令δ是x2-x+1的根,则δ是Fq2上6重根,所以δ3=-1。所以: x3+1=(x-δ)*(x-δ3)*(x-δ5)=(x+1)*(x2-x+1), (x+1)和(x2-x+1)是Fq[x]上的自反多项式,所以 xn+1=(x3+1)7s=(x+1)7s*(x2-x+1)7s, 所以Fq上长度为n=3·7s的斜循环码中LCD码的个数为(7s+1)2。 由于引入了自同构映射,在斜多项式环中定义了新的乘法运算,把λ-常循环码存在LCD码的存在性证明推广到斜λ-循环码。考虑到不同的自同构映射会产生的不同结果,寻找合适的自同构映射成为解决问题的一个关键点。本文得出了LCD码在有限域上的斜λ-常循环码中存在的充要条件,以及λ≠±1时,利用线性空间的理论来讨论斜λ-常循环码中的LCD码,给出LCD码存在的充要条件,并且讨论了有限域上斜循环码中LCD码的计数问题。 λ-常循环码上的相关结论(定理、性质)是否能推广到斜λ-常循环等理论上,取决于码的代数结构是否一致。由于定义的映射不同,在同一个多项式环上可能LCD码的存在性和性质也不相同。由于引入了自同构映射,在多项式商环中定义了新的乘法运算。研究时由于乘法交换律不再成立,相关的运算会比较繁琐,同时该码的生成矩阵也会更复杂,需要寻找新的算法。将代数的方法用在斜λ-常循环码中LCD码的研究上,引入自同构映射,丰富了纠错码的理论,拓展了可寻求好码的范围。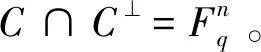
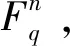
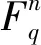
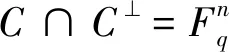
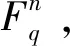
3 有限域上斜循环码中LCD码的计数问题
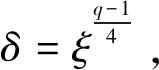
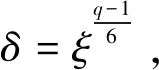
4 结论

