利用累积量理论量化双模压缩贝尔态的非高斯特性

向少华， 赵宇靖

(怀化学院 机械与光电物理学院，怀化 418008)

1 Introduction

The non-Gaussianity plays an important role in a variety of fields including classical probability theory and statistics[1], biology science[2], and signal processing[3,4]. Especially, in the quantum information science a non-Gaussianity has already been adopted to quantify the deviation of quantum states or phase-space distribution functions from the Gaussian counterparts with or without the aid of physical transforms. In order to quantify this property, the various measures have been suggested in recent years. Genoni et al. first used the Hilbert-Schmidt distance to quantify the non-Gaussian character of a bosonic quantum state and evaluated the non-Gaussianity of some relevant states[5]. Subsequently, they developed the entropic measure of non-Gaussianity based on the quantum relative entropy[6], by which they investigated the performance of conditional Gaussification toward twin-beam and de-Gaussification processes driven by Kerr interaction. Additionally, a quantum non-Gaussianity witness in phase space was proposed to discriminate between quantum non-Gaussian states and mixtures of Gaussian states, whose main idea is to seek the violation of a lower bound for the values that the phase-space quasi-probability distributions can take in a particular point of phase space[7,8], where the Husimi Q-function-based witnesses is shown to be more than effective than other criteria in detecting quantum non-Gaussianity of various kinds of non-Gaussian states evolving in a lossy channel[8]. However, it should be pointed out that the computation of these measures is intractable for multimode continuous-variable (CV) non-Gaussian entangled states since it requires to look for the exact target Gaussian state. Thus, a natural question arises:Are there other simple ways to measure the non-Gaussianity of such multimode CV non-Gaussian entangled states? If so, how does one measure it?

Our answer is yes. This challenge could be tackled by introducing the cumulants to determine the non-Gaussianity. We will call it the cumulant-based non-Gaussianity. The motivation of the measure being proposed is due to two facts:(i) In probability theory and statistics, the higher-order cumulants have been recognized as a good measure of quantifying statistical characteristics of the probability distribution. For a univariate case, the third-order (or called skewness) is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean, while the fourth-order cumulant (or called kurtosis) provides a measure of the distance to Gaussianity. Positive kurtosis indicates heavy tails and peakedness relative to the Gaussian distribution, whereas negative kurtosis indicates light tails and flatness. Namely, the larger the kurtosis is different from zero, the more highly the distribution is non-Gaussian. The multivariate skewness and kurtosis measures were also developed to assess departure from multivariate normality[9-12]. (ii) The characteristic function to any quantum operator including the density matrix operator can be expanded by its cumulants[13]. A quantum operator is Gaussian if all the cumulants of greater two orders of its characteristic function vanish identically; otherwise, it is non-Gaussian. It suggests that a non-Gaussianity of quantum state can be measured by the higher-order cumulants. Therefore, here we will mainly concentrate on the fourth-order cumulant of quantum states to its non-Gaussianity. In addition, as stated in Refs.[5-7], the non-Gaussianity of quantum state based on the geometric and entropic distances is invariant under the Gaussian operations. Thus, we present another problem by intuition:Could the cumulant-based non-Gaussianity of quantum states remain unchanged under some Gaussian operations such as two-mode squeezer?

In the present paper, we mainly study the non-Gaussianity of two-mode squeezed Bell states, which can be generated by operating with two-mode squeezer on Bell states, thus allowing us to discuss the influence of Gaussian operation on non-Gaussian entangled states. The remainder of this paper is organized as follows. In Section 2, we define the cumulants of a quantum state in the characteristic function representation and provide an explicit formula for cumulants of any order. We illustrate in section 3 how two-mode squeezer effects the non-Gaussianity of quantum state using two examples of two-mode squeezed Bell states. We conclude with a summary and outlook in section 4.

2 Higher-order cumulants of quantum non-Gaussian states

(1)

Generally speaking, the characteristic function of any continuous-variable quantum state can be expressed as in the following form:

χ[ρ](ξ)=f(ξ)χG(ξ)

(2)

We see if the functionf(ξ) is a constant, then a state described by Eq.(2) is Gaussian one; otherwise, it is a non-Gaussian state.

Another equivalent description of a probability distribution is through the cumulant generating function, which is the logarithm of the moment-generation function:

Γ(ξ)=lnχ[ρ](ξ)

(3)

Onceχ[ρ](ξ) is known, thekth-order cumulant can be generated by evaluating thekth derivative of Γ(ξ) atξ=0 and is given by

(4)

It is obvious from Eqs.(1) and (2) that the Gaussian component is treated equivalently to aN-mode Gaussian stateρG, whose characteristic function is fully determined in the phase space by the first and second moments of the quadrature operators[16]

χ[ρG](ξ)≡Tr[ρGD(ξ)]

=exp[-ξVξT-i〈d〉ρGξT]

(5)

Thus, in terms of the definition of cumulant, one can easily show that the first-order cumulants are given by

C1(ξj)=〈dj〉ρG

(6)

and the second-order cumulants are the vectors of the covariance matrix, i.e.,

C2(ξlξm)=vec(Vl,m), (l,m=1,2,…,2N)

(7)

whereξldenotes thelth component of vectorξ.

In the following, we will mainly focus on the cumulant forf(ξ), whose most natural choice is

(8)

wherealm…are the expansion coefficients of Eq.(8).

(9)

Comparing Eq.(8) with Eq.(9), we have

(10a)

(10b)

Finally, we can write thekth-order cumulants of the functionf(ξ)| in a compact form:

(11)

wherepruns through the list of all partition of {1,2,…,2N},Bruns through the list of all blocks of the partitionp, and |p| is the number of parts in the partition. This is the main result of our work. Therefore, once the characteristic function of quantum state is known, one can easily obtain its cumulants of arbitrary order via the formulas (6), (7) and (11). Especially, it is much easier for us to obtain the higher-order cumulants of quantum state in terms of the formula (11) since all cumulants of greater than two for Gaussian functions vanish identically, greatly simplifying the calculation process. As has been stated before, we will use the non-vanishing fourth-order cumulant to measure the non-Gaussianity for any quantum states, which can be readily expressed as

2alamakh[6]-6alamanah

(12)

where the number in the square bracket represents the number of erms in the combination as the indices rotate, e.g.l→m,m→n,, etc.

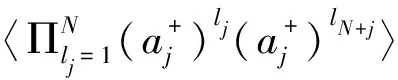
(13)

For the case ofl1=…=l2N=1, we have the followingNth-order correlation function for first-power numbers of photons

(14)

By means of the cumulant theory, we can reveal the statistical properties of such a second-order correlation function for Bose operators.

3 Cumulants of two-mode squeezed Bell states

In this section, we are interest in two classes of two-mode non-Gaussian entangled states:squeezed single- and two- photon Bell states, respectively. Our choice is based on two facts. One fact is that these states are of important in quantum information science such as CV quantum teleportation[17,18]and the possible experimental schemes for generating these states was proposed in Refs.[19-21]; another fact is that these states can provide a good example for testing our question in the introduction section. They can be viewed as a superposition of two-mode squeezed states. Note that two-mode squeezer has already been realized experimentally in Ref.[22], belonging to a Gaussian transformation, while the Bell state is two-qubit maximally entangled state, belonging to non-Gaussian state.

We first consider a case of two-mode squeezed single-photon Bell state, which is given by

(15)

Applying the following formula

(16)

we can readily obtain the corresponding characteristic function as

(17)

in which a 2×2 covariance matrixVSBis given by

(18)

and the functionfI(ξ1,ξ2) is calculated to be

(19)

We see that the second part in Eq.(17) is equal to the characteristic function of two-mode squeezed vacuum state[23], while the functionfI(ξ1,ξ2) has quadratic form in such a way that all its odd cumulants are nullified. In order to analyze the cumulant-based non-Gaussianity, we only need to know all the fourth-order cumulants of the state (15) and then, according to the formula (11), we can obtain the following fourth-order non-zero cumulants:

(20a)

(20b)

(20c)

(20d)

(20e)

(20f)

Let us return to consider the second class of non-Gaussian entangled states:two-mode squeezed two-photon Bell state, which can be written as

(21)

Using the same method as above, we can easily obtain the characteristic function of the state (21) as

(22)

whereVSBis given by Eq.(18) and the functionfII(ξ1,ξ2) is calculated to be

eiφsinh2(r)-sinh(2r)]ξ1ξ2+

(23)

We see from Eq.(23) that since the functionfII(ξ1,ξ2) is quartic form, all odd cumulants are nullified. Using the formula (11), we can obtain the fourth-order non-zero cumulants as

(24a)

(24b)

(24c)

(24d)

whereg(r,φ)=e-iφcosh2(r)+eiφsinh2(r)-sinh(2r). All the remaining fourth-order cumulants vanish completely. From these cumulants we can arrive at the same result as above. That is, the cumulant-based non-Gaussianity of quantum state can change under the transformation of two-mode squeezer.

Fig. 1 The fourth-order cumulant of the second-order correlation function as a function of two-mode squeezing degree when two mode are in a Non-Gaussian entangled state. The solid line is for two-mode squeezed single-photon Bell state (15). The dashed and dot-dashed lines are for two-mode squeezed two-photon Bell state (24) with φ=π and φ=0, respectively.

We end this section with the following remarks. First, we address the question presented in the introduction. As is well known, a Gaussian transformation can map Gaussian input states into Gaussian output states. Namely, Gaussian operations do not change the Gaussian character of a quantum state and as a result its non-Gaussianity remains invariant, no matter what type of non-Gaussianity measures one uses. Nevertheless, we will emphasize that Gaussian operations can vary the amount of non-Gaussianity, which is tightly connected to the shape of the phase-space distribution functions. For example, under the action of Gaussian transformationUGdescribed by (X,Y), the input-output characteristic function of an arbitrary state is given byχin(ξ)(Xξ) exp (-ξYξT)[24-26]. It follows that Gaussian operations can skew the Boson operators' distribution functions of non-Gaussian quantum states, thus giving rise to a strongly sub-Gaussian and demonstrating that two modes can be more non-Gaussian. Second, the proposed method is a very general and can be applicable in other contexts. e.g., Bose-Einstein condensate[27-28]and optomechanical systems[29,30], or other quantum entangled states such as W/GHZ coherent entangled states[31]. Finally, just as stated in Ref.[32], the fourth-order cumulant can be regarded as an indicator of testing non-Gaussian behavior for the probability distribution of the quadrature amplitudes. The larger the absolute values of the cumulants, the more significant the distribution departs from Gaussianity, meaning that it is much useful for quantum information processing and quantum computation. Thus our analysis is of important for correctly infer on the non-Gaussian natures of some non-Gaussian states in the physical process.

4 Summary and conclusions

In summary, we have proposed a tactics for characterizing non-Gaussianity of quantum state based on the cumulants. Unlike the other geometric and entropic distances, our measure only need to focus on the non-Gaussian component of the characteristic function, thus greatly simplifying the process of calculation. We have investigated the influence of two-mode squeezer on the non-Gaussianity of four Bell states. Our analysis shows that the non-Gaussianity does not remain invariant under applying Gaussian transformation and as a consequence, these quantum states exhibit the highly non-Gaussian behavior. Namely, the squeezing action is helpful in enhancing the non-Gaussianity of non-Gaussian entangled states. We hope that our work opens the way for more detailed studies of the non-Gaussianity of complex quantum systems.