基于图的粗糙集属性约简方法

米据生,陈锦坤

(1.河北师范大学 数学与信息科学学院, 河北 石家庄 050024;2.河北省计算数学与应用重点实验室,河北 石家庄 050024;3.闽南师范大学 数学与统计学院,福建 漳州 363000)

自1982年Pawlak[1]提出粗糙集理论以来,该理论已成为一种有效处理不确定和含糊信息的重要数学工具。在数据挖掘、机器学习和知识发现等领域有重要的应用[2-5]。

由于在现实数据集中,往往存在大量冗余和不确定性的信息,严重影响到后续数据挖掘和处理的效率。因此,如何高效地去掉冗余信息,已成为当前数据分析处理的一个热点问题。作为粗糙集理论的一个重要应用,属性约简已经被证明是一种有效的数据约简方法。它通过删除冗余属性,能获得数据集合的本质信息和保持原始数据分类信息的完整性,从而提高数据的分类质量。

基于区分矩阵和布尔推理方法计算所有的属性约简或最小约简已经被证明是一个NP-hard问题[6]。因此,各种高效的启发式约简算法被提出[7]。这些启发式的约简算法主要是寻找一个约简或近似约简。常用的启发式约简算法主要包括:基于区分矩阵的约简算法[8-10];基于正域的约简算法[11-13]和基于信息熵的约简算法[14-17]。关于粗糙集的属性约简方法的系统阐述可参阅综述文章[7,18]。

目前粗糙集属性约简方法的研究已经取得了很多成果。然而,这些算法在处理大规模数据集,尤其是面对高维数据时,效率仍然不够理想。针对以上问题,本文提出一种新的属性约简框架。主要是受到文[19-20]的启发,从图论的角度出发,对决策信息表的区分矩阵给出直观和等价的刻画,最后利用极小顶点覆盖方法获取决策表的属性约简。数值实验结果表明,所提出的基于图论的属性约简方法在面对较大规模数据集时具有有效性和高效性。

1 基本知识

1.1 属性约简

定义1[21]称S=(U,A)是一个信息系统,其中U和A分别是非空有限论域和属性集;对于任意的属性a,称a:U→Va是信息函数,满足:∀x∈U,a(x)∈Va,其中Va称为属性a的值域。

对任意的B⊆A,记

IND(B)={(x,y)∈U×U|a(x)=a(y),∀a∈B},

显然IND(B)是U上的一个等价关系,也称为不可分辨关系,它能导出U上的一个划分:

U/B={[x]B|x∈U},

其中,[x]B={y|(x,y)∈IND(B)}称为x关于IND(B)的等价类。

给定一个信息系统S=(U,A)和X⊆U,X关于IND(B)的下、上近似分别定义为:

定义2[21]决策表是一个特殊的信息系统S=(U,C∪{d}),其中C为条件属性集,d∉C为决策属性。记IND(d)是由决策属性d所导出的等价关系,而U/d是由IND(d)生成的划分。

设S=(U,C∪{d})是一个决策表,定义如下不可分辨关系:

IND(B|d)={(x,y)∈U×U|(∀a∈B,a(x)=a(y))∨(d(x)=d(y))}。

称B是S的一个约简,若满足:

所有约简的交称为S的核心属性集。

定义3[22]设S=(U,C∪{d})是决策表,∀x,y∈U,称

M(x,y)=

为x与y的区分集。所有的区分集可形成一个对称矩阵M,称为决策表S的区分矩阵。

利用区分矩阵,便可以定义相应的区分函数,从而获得所有的约简集。

定义4[23]设M为决策表S=(U,C∪{d})的区分矩阵,则称

fM=∧{∨M(x,y)|∀x,y∈U,M(x,y)≠∅}

为M的区分函数。

1.2 图的极小顶点覆盖

一般地,一个无向图可表示为一个二元组G=(V(G),E(G)),其中V(G)是图G的顶点集,E(G)是图G所有边的集合[25]。为简单起见,一般可把图简写为G=(V,E)。图G中边的端点若重合为一个顶点,则称为环。若两条边有相同的端点,则称这两条边是平行边或重边。称图H是图G的子图,记为H⊆G,若满足V(H)⊆V(G)且E(H)⊆E(G)。设G1和G2是图G的两个子图,称G1∪G2为图G的并图,其顶点集和边集分别为V(G1)∪V(G2)和E(G1)∪E(G2)。给定图G的顶点v,dG(v)表示G中与顶点v相连接的边的数目,称为顶点v的度。

定义5[25]设G=(V,E)是给定的图,K⊆V。若K能覆盖图G的所有边(即E的每条边都与K中的某个顶点相连接),则称顶点子集K是图G的一个顶点覆盖。进一步地,对于任意的v∈K,若K-{v}不是图G的顶点覆盖,则称K是图G的极小顶点覆盖。

类似于求决策表的所有约简,图的所有极小顶点覆盖也可以通过构造相应的布尔函数获得[20,25]。

fG=∧{∨N(e)|∀e∈E},

N(e)是与边e∈E相连接的顶点集。

2 基于图的属性约简框架

2.1 决策表的诱导图

定义6[19-20]设S=(U,C∪{d})是决策表,M是S的区分矩阵,为了方便,用e∈M表示e是矩阵M中的元素。记

V=C,E={e∈M|e≠∅},

则称GS=(V,E)是决策表S的诱导图。

从定义6可以看出,决策表S的诱导图实际上是以决策表的条件属性作为顶点集,而以区分矩阵M的非空元素作为边集。它是对决策表的区分矩阵的一种直观刻画。通过这种刻画,以及利用引理1和引理2,易知决策表S的所有属性约简集与该诱导图的所有极小顶点覆盖集是相同的[19-20]。从而,求决策表的属性约简问题可转化为求相应的图的极小顶点覆盖问题。这为粗糙集的属性约简方法提供了新的视角和方法。

例1表1是一个决策表S=(U,C∪{d}),其中U={x1,x2,x3,x4},C={a1,a2,a3}。由定义3,可获得其区分矩阵M(见表2)。在表2中,a2a3表示集合{a2,a3}。从而,由引理1,易知S有两个约简集,分别为{a1,a3}和{a2,a3}。

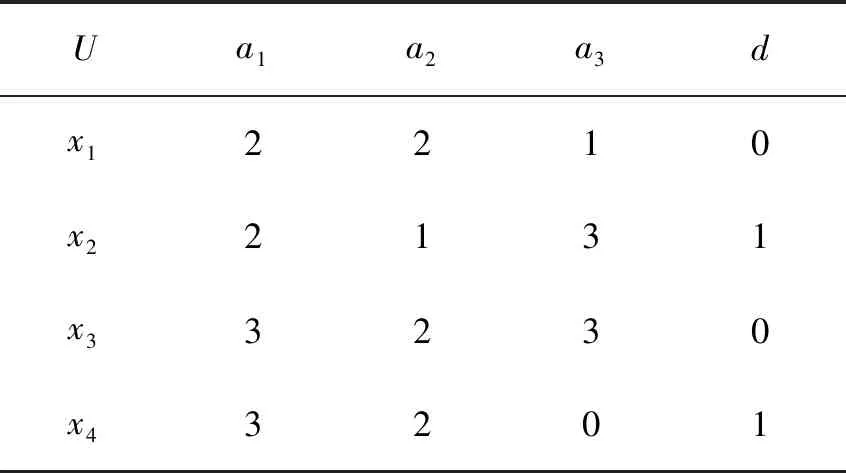
表1 例1的决策表Tab.1 A decision table of Example 1

利用定义6,其诱导图GS见图1。在图1中,GS共有4条边,对应了区分矩阵M的4个非空且不重复的元素。

表2 表1的区分矩阵Tab.2 Discernibility matrix of Tab. 1

图1 表1的诱导图Fig.1 Induced graph of Tab.1

由于区分矩阵M是对称矩阵,并且M中往往有很多重复的元素。定义6蕴含了去掉这些重复的元素。因此,定义6所导出的图是不包含平行边的。实际上,如文献[20]所述,利用吸收律,上面的诱导图可以进一步的简化。

由于平行边对获取图的顶点覆盖没有影响,因此,为计算的方便,可以得到下面更一般的诱导图(见定义7和图2)。

定义7设S=(U,C∪{d})是决策表,M是S的区分矩阵。记

V′=C,E′=M-{∅}

定义6和定义7中所定义的两种诱导图的区别仅仅是去掉一些重复的边(或平行边)。实际上,图1可看成是图2的简化(或子图)。而且,这两个图的极小顶点覆盖集是相同的(见性质1)。记C(G)表示图G的所有极小顶点覆盖集。

图2 表1的一般诱导图Fig.2 General induced graph of Tab.1

证明由定义6、定义7和引理2即可证得。

性质2GS=(V,E)是决策表S的一般诱导图,若a∈C是S的核心属性,则a在图GS中是带环的顶点。

证明由相关的定义即可证得。

2.2 一般诱导图的分解和约简方法

定义7所给出的一般诱导图本质上是对决策表的区分矩阵的刻画。但是一个决策表的区分矩阵往往需要O(|U|2|C|)的存储空间,这也意味着生成整个诱导图也需要O(|U|2|C|)的存储空间。这对于具有较大样本集的决策表而言,易因存储空间的不足而导致其算法极其低效。因此,本文避免生成整个诱导图,而是通过局部的思想,对其子图进行分步处理。

定义8设GS=(V,E)是决策表S=(U,C∪{d})的一般诱导图。对于任意的x∈U,记

Vx=V,Ex={M(x,y)|y∈U},

则Gx=(Vx,Ex)是GS的一个子图。

证明由定义3、定义7和定义8即可证得。

定理1表明决策表的一般诱导图可分解为一些子图的并。

例2在例1中,对于x1∈U,其子图Gx1见图3(a)。显然,Gx1是GS(图2)的一个子图。由图2,易知GS恰好分解为4个子图。

图3 GS的子图Fig.3 Subgraphs of GS

证明由定义8和定理1即可证得。

3 基于图的属性约简算法

由上一节的理论结果,本节将设计相应的启发式算法来获得决策表的主要属性。通过改进经典的图顶点覆盖算法[26],我们有下面基于图的粗糙集特征选择算法。

算法1基于图的粗糙集特征选择算法1(GRF1)

输入:决策表S=(U,C∪{d})

输出:一个属性约简Red

1) Red=∅

2) 生成诱导图GS=(V,E);∥根据定义6

whileE≠∅

v0=arg max{dG(v)|v∈V};

Red←[Red,v0];

去掉E中被Red所覆盖的边,并仍记为E.end while

3) for每个v∈Red

if Red-{v}能覆盖简化图G的所有边

Red←Red-{v};

end if

end for

算法1(GRF1)的空间复杂度是O(|U|2|C|),与其他基于区分矩阵的约简算法的存储空间基本是一致的。其次,GRF1的时间复杂度是O(|U||C|)。与其他大部分的约简算法相比,GRF1显然更加快速。但是面对大规模数据集,尤其是含有较大样本的数据集时,GRF1容易因为内存不足而导致无法运行。

算法2基于图的粗糙集特征选择算法2(GRF2)

输入:决策表S=(U,C∪{d})

输出:一个近似属性约简Red

1) Red=∅

2) for 对每个x∈U

生成子图Gx=(Vx,Ex);//定义8

Red←[Red,v0];

end while

end for

算法2(GRF2)的时间和空间复杂度都是O(|U||C|),与其他基于区分矩阵的约简算法和GRF1相比,其存储空间降低了很多。这将会极大地提高GRF2的运行效率。但是与GRF1相比,GRF2不一定获得一个真正的约简,它所获得的特征数目往往比GRF1多。

4 实验结果与分析

实验选用了8个公开的数据集进行验证。具体的数据集描述见表3。在实验中,我们选取了3种具有代表性的约简算法进行对比,它们分别是基于区分矩阵的约简算法SPS[10]、基于正域的约简算法FPR[13]和基于信息熵的约简算法FCCE[13]。本文所有的实验结果均在Windows 10 (i7-6700,CPU 3.40 GHz,内存24GB)的普通个人PC上获得,使用的操作平台是Matlab2016b和Weka3.8。

具体的实验结果如图4、表4、表5、表6、表7和表8所示。图4展示了GRF1和GRF2这两种算法在生成相应的图时所需要的存储空间。从图4可看出,GRF2所需要的存储空间比GRF1小很多,比如,对于数据集Chess,GRF2所占用的存储空间仅仅是GRF1的0.13%。对于拥有大样本的数据集而言,这种差异往往会更加明显。以数据集Letter和Relathe为例,算法GRF1会因为“内存溢出”而导致程序无法运行。实际上其他基于区分矩阵的算法也往往具有这种现象。比如,算法SPS,虽然它已经去掉了区分矩阵中一些不必要的元素,但是对于较大规模的数据集比如Letter而言,它仍然会因为内存的不足而导致无法获得实验结果。因此,与其他基于区分矩阵的属性约简算法相比,GRF2更适合于处理大规模的数据集。实际上,GRF2和FPR,FCCE等算法的存储空间复杂度都是一样的。它们都适合于处理大样本的数据集。

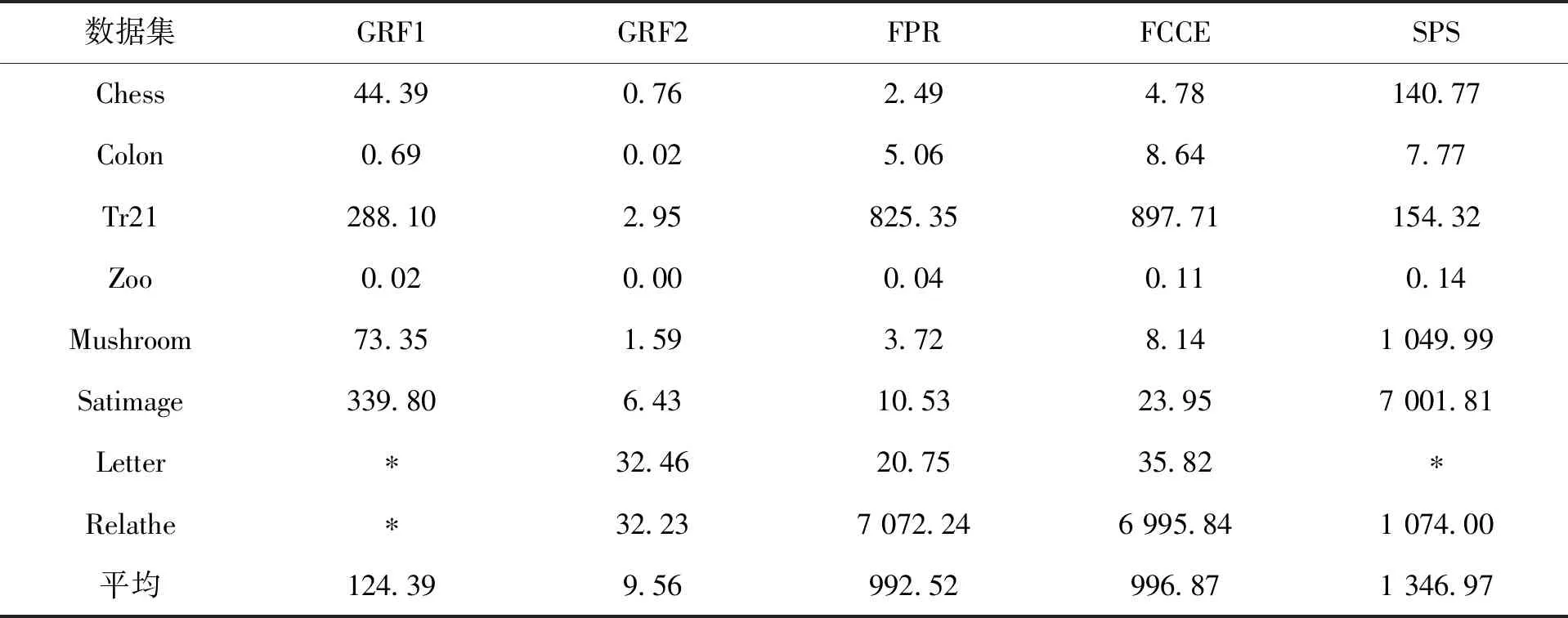
表4记录了5种算法在这8个数据集上的运行时间。在表中,“*”表示由于该算法“内存溢出”而导致的程序无法运行。从表4中可看出,GRF1和SPS适合于处理高维小样本的数据集。FPR和FCCE适合于处理低维大样本,而GRF2不管什么类型的数据集,其运行速度均表现得极其高效。以Relathe数据集为例,GRF2的运行时间分别是FPR,FCCE和SPS的0.46%,0.46%和0.30%。这些结果进一步表明GRF2是一种高效的特征选择方法。

表5列出了具体的约简结果。从表中可知,与其他算法相比,GRF1和FCCE均能获得极小的属性子集。实际上它们均能获得一个真正的约简集。

而GRF2只能获得一个协调集,平均而言,GRF2获得的特征子集的属性个数是最大的。然而,对于大部分的数据集而言,这种差异并不是很大。

表6,表7和表8分别记录了这5种算法在约简前后的分类精度。在这些表中,“Full”表示约简前原始数据的分类精度。所有的分类精度均在Weka3.8上采用10折交叉验证获得,实验中采用了3种分类器:CART,SVM和PAPT。实验结果表明,与原始数据集的分类精度相比,这些约简算法均能获得较好的分类精度。这也表明这些算法能提取一些重要的特征。与FPR,FCCE和SPS相比,GRF1和GRF2获得较好的平均分类精度。尤其是GRF2,在大部分的数据上,均能获得最好的分类精度。

表3 实验数据集Tab.3 Data sets for test

图4 算法GRF1和GRF2的存储空间Fig.4 Storage spaces of GRF1 and GRF2

秒/s

表5 约简结果Tab.5 Results of reduct

表6 分类精度(CART)Tab.6 Classification accuracy (CART)

表7 分类精度(SVM)Tab.7 Classification accuracy (SVM)

表8 分类精度(PAPT)Tab.8 Classification accuracy (PAPT)

5 结 语

本文基于图的顶点覆盖方法提出了一种粗糙集属性约简模型。该模型对经典粗糙集的区分矩阵进行了直观的刻画,并把相应的属性约简问题转化为其诱导图的极小顶点覆盖问题。进一步地,利用图论中的理论方法,设计了两种启发式的属性约简算法。实验结果表明,所提出的约简算法不仅可以选择少量的主要特征,而且能保持甚至提高约简数据的分类精度。尤其是所提出的GRF2算法,能高效的处理大规模的数据集。但是,GRF2所提取的特征个数仍然较多,因此,如何进一步去掉一些冗余的特征,这将是我们后续的主要工作之一。