由反对称化操作探究Levi-Civita与Kronecker符号的性质
彭俊金,雷良建
(1.贵州师范大学物理与电子科学学院,贵州 贵阳 550001;2. 贵州省射电天文数据处理重点实验室,贵州 贵阳 550001)
Levi-Civita(简称L-C)符号(张量)是以著名的意大利籍数学与物理学家Tullio Levi-Civita的姓氏命名的一个量。当时空或空间的维度为n时,L-C符号定义为一个含n个逆变或协变指标的完全反对称量[1-6],并约定所有非零分量的取值为1或-1,而L-C张量由L-C符号乘上一个仅与度规张量行列式有关的因子得到。它们在微分几何、群论、经典力学、电磁理论、量子力学、量子场论与广义相对论[1-6]等中有着非常广泛且重要的应用。特别地,借助三维L-C符号可以很方便地描述经典力学、电动力学与量子力学等中的一些物理量与规律[7]。而在L-C符号(张量)的众多应用中,时常会涉及到Kronecker delta符号(简称为Kronecker 符号)这一个数学与物理学中常见的重要量。因此,掌握它们各自的性质与应用以及建立二者之间的联系都是值得关注的问题。
本文直接由度规行列式基于各分量的定义出发,借助于由Kronecker符号与L-C符号之间取反对称化操作而得到的恒等式,推导得出L-C符号(张量)与Kronecker符号之间的一个重要表达式。为了深入理解重要表达式的意义,进一步探讨了如何由它导出文献中常见的两个重要推论;并在此基础上,分析了二者的性质并尝试给出其它证明方法。本文结果有利于物理,特别是广义相对论学习者系统、全面地理解L-C符号(张量)与Kronecker符号的性质。
1 重要表达式
下文中,基于n维时空中度规张量gμν的行列式定义为
g=det(gμν)
(1)
将证明在理论物理,如广义相对论、弦论以及修正引力理论中常用的由两个L-C张量的(n-m) (0≤m≤n)个指标缩并而得到的一个重要表达式[1-6]:
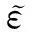
(2)
或由L-C符号等价表示为
εμ1···μn-mα1···αmεμ1···μn-mβ1···βm
(3)
采用数学归纳法证明(3)式,提供一个便于物理,尤其是广义相对论学习者易于理解的详细证明,并剖析其一些重要性质。具体步骤为:首先由n维时空的度规张量行列式,得到m=0情形的结果;在此基础上,再次验证m=1,2这两种特殊情形;最后证明它们在一般情形下仍然成立。证明过程的核心是:对Kronecker符号的上指标与逆变L-C张量的所有指标进行反对称化操作,由此得到一个零值恒等式,然后展开该式来实现指标轮换。
2 m=1情形
首先,令度规行列式的定义式(1)两边同时除以g并乘上n!即可得到两个L-C符号所有指标缩并后的结果:
εμ1μ2···μnεμ1μ2···μn=n!
(4)
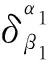
(5)
对上式进行展开,进一步得到
(6)
让协变L-C符号εμ1···μn与上式进行所有指标缩并,有
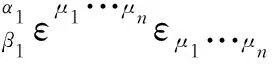
=nεμ1···μn-1α1εμ1···μn-1β1
(7)
最后,代入(4)式化简上式,可以得到(3)式在m=1情形的结果:
(8)
此外,(8)式也可直接由度规张量分量的代数余子式导出[8]。
3 m=2情形
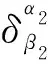
(9)
展开(9)式,有
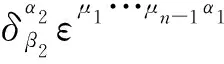
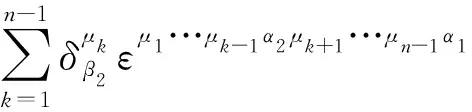
(10)
对上式与εμ1···μn-1β1的指标μ1,μ2,···μn-1进行缩并,得到
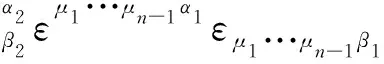
=(n-1)εμ1···μn-2α1α2εμ1···μn-2β1β2
(11)
利用(8)式化简,整理可得m=2时的结果,即
(12)
也就是说,当m=2时(3)式仍然成立。
4 一般情形
重复上述m=1,2时的操作,不难验证m=3,4,5,6等时(3)式仍然成立。在此基础上,不妨假设(3)式在(m-1)时成立,即
εμ1···μn-m+1α1···αm-1εμ1···μn-m+1β1···βm-1
(13)
这里以及下文中,系数λ=(m-1)!(n-m+1)!。
根据数学归纳法的要求,基于(13)式,如果能够证明m情形仍然成立,则(3)式在一般情形下亦成立。
同理,由反对称化Kronecker符号与指标在上的L-C符号的乘积即可得到恒等式
(14)
对其进行展开,有
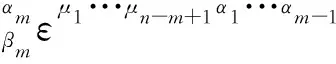
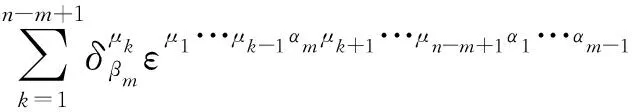
(15)
同样,让(15)式与εμ1···μn-m+1β1···βm-1之间进行μ1,···,μn-m+1等指标缩并,得到
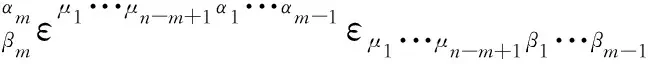
=(n-m+1)εμ1···μn-mα1···αmεμ1···μn-mβ1···βm
(16)
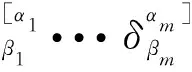
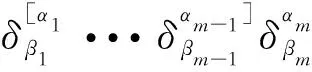
(17)
对(16)式化简,我们最终得到与(3)式完全一样的结果或等价表示为含L-C符号与度规张量分量的表达式
gg[α1|β1|···gαm]βm
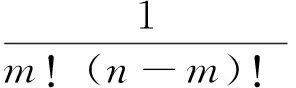
·εμ1···μn-mα1···αmεν1···νn-mβ1···βmgμ1ν1
···gμn-mνn-m
(18)
当m=1时,(18)式正好是文献[8]中给出的基于度规张量各分量的代数余子式。因此,从某种意义上来说,(18)式可看作代数余子式的一般推广。
作为(2)或(3)式的一个简单应用,可以考虑两个三维的L-C符号之间的乘积,有这样一些具体结果:
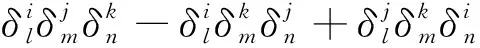
(19)
为了得到(6)、(10)、(15)与(17)式,必须对反对称指标进行降阶处理。其实质是对完全反对称量V[σTα1···αm](Tα1···αm完全反对称)按Vσ进行展开。为此,定义一个新的量
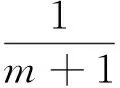
(20)
不难证明,Yσα1···αm的指标σ与任意αi交换顺序后其取值反号。因此,Yσα1···αm=Y[σα1···αm]完全反对称。反对称化(20)式可得Y[σα1···αm]=V[σTα1···αm],由此可导出V[σTα1···αm]的展开式,展开式恰好为(20)式的右边部分。(17)式可应用于Gauss-Bonnet引力模型的场运动方程的化简[9]以及Lanczos-Lovelock引力[4]性质的探讨,如:守恒量与全息对偶等等。因其重要性,我们会在第6节进一步论述(17)式的推导与应用。
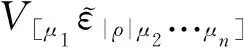
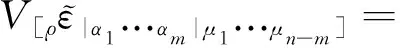
(21)
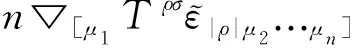
5 两个推论与推广的Kronecker符号的性质
在本节中,我们讨论由(2)式延伸出来的两个重要推论,并深入挖掘L-C符号(张量)与Kronecker符号的性质。为方便起见,引入文献中常见的符号约定,即推广的Kronecker delta符号[6]
(22)
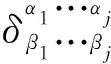
(a)它的值域为{-1,0,1};
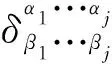
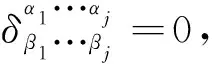
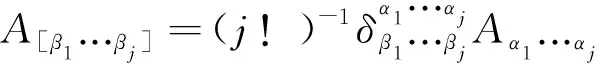
(f)完全反对称化任意两个推广的Kronecker符号的乘积可得
(23)
不难验证,由(23)式也可导出(22)式,因此,二者彼此等价。也就是说,(23)式也可用来定义推广的Kronecker符号;
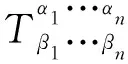
可表示为
(24)
上式中f为时空坐标的任意标量函数;
(h) 当两个推广的Kronecker符号的指标之间存在如下缩并关系时,有
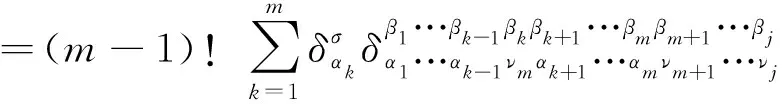
(25)
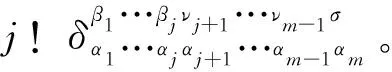
当m=n时,利用(22)式中的符号约定,由(2)式直接可给出如下推论一:
(26)
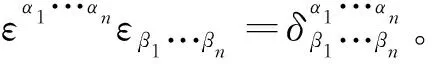
特别地,当(26)式中有(n-m)个指标缩并时,可得
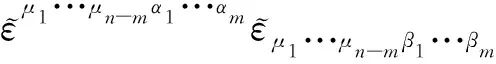
(27)
比较(2)与(27)两式,又导出本文推论二,即一个有关推广的Kronecker符号的重要关系式:
(28)
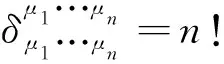
下面,我们举例说明(26)和(28)式的三个重要应用。首先,在推广的Kronecker符号的性质(e)的帮助下,利用(26)和(28)式、或直接应用推广的Kronecker符号的性质(h),将(21)式表述成如下的等价形式:
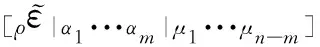
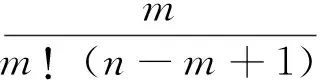
(29)
当(26)式中所有逆变指标α1···αn或协变指标β1···βn取值为1···n时,我们可以得到上与下指标的L-C符号由推广的Kronecker符号表示的结果:
(30)
由此可见,这两类符号具有天然的联系性。当然,上式也可直接由(22)式给出。有了(30)式,可以更方便地理解n维方矩阵M的行列式定义,这是因为
|M|=n!M[1|1|M2|2|···Mn]n
=εμ1···μnMμ11···Mμnn
(31)
式中,第二个等式的导出是基于上述推广的Kronecker符号的性质(e)完成的,最后一个等式是行列式最为常用形式之一。在(31)式的基础上,再次进行同样操作,可得
|M|=εμ1μ2···μnMμ1[1M|μ2|2···M|μn|n]
=(n!)-1εμ1···μnεν1···νnMμ1ν1···Mμnνn
(32)
(32)式正好是本文证明(3)式的出发点。最后,(30)式还可用来推导对偶坐标基底{dxμ}的楔形积(wedge product)的变换关系,即
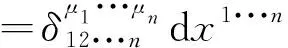
=εμ1···μndx1···dxn
(33)
上式中dxμ1···μn是dxμ1∧···∧dxμn的简写,类似结果可参考文献[10]。
6 (26)与(28)两式的又一证明
本节中,我们将通过行列式与矩阵的形式给出(26)和(28)式的又一更为直观的证明。首先,考虑(26)式的证明。定义一个j×j的方矩阵M为
(34)
(35)
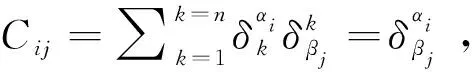
(36)
因此,det(C)=det(A)det(B),也就是
(37)
进一步利用L-C张量的定义,即可得到(26)式。
接下来,证明(28)式。同样,引入一个n×n方矩阵Z,其分块矩阵表示为
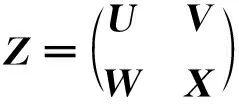
(38)
式中,对角元方矩阵U与X分别定义为
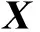
(39)
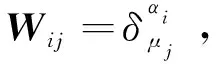
(a) 所有αi与βk各自取值互不相同,同时还需满足全部αi的取值集合Sα与所有βk的取值集合Sβ完全一致,即Sα=S0=Sβ。S0记为{1≤s1≠s2≠···≠sm≤n}。
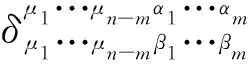
det(Z)=det(U)det(X-WU-1V)
(40)
因需det(U)≠0,可得det(Z)=det(U)det(X),即
(41)
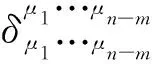
(b) 其余αi与βk的取值。
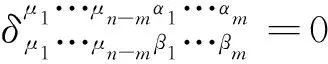
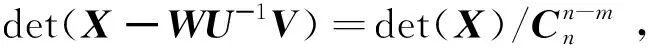
基于对Kronecker符号与L-C张量的反对称化操作、或借助矩阵与行列式的性质,本文分别给出了三种推导(26)与(28)式的方法。很显然,本节中给出的证明最为直观、简单。
最后,我们将推导(28)式的推广形式。如果对(34)式中矩阵M的行列式按第j列执行拉普拉斯展开,我们又可得到(17)式由推广的Kronecker符号表示的结果:
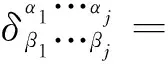
(42)
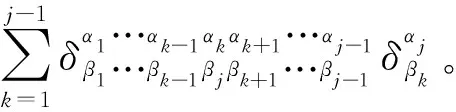
(43)
(44)
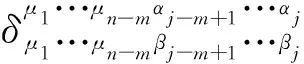

7 结 论
本文直接由n维时空或空间中度规张量的行列式的基本定义(1)式出发,得到了恒等式(14)式,并分别在m=1,2以及一般情形下证明了Levi-Civita符号(张量)与Kronecker符号之间的具体联系,即二者满足(2)或(3)式。在此基础上,引入推广的Kronecker符号,给出了两个重要推论(26)与(28)式。需要注意的是,仅利用(42)式或矩阵的性质,还可以导出一个比(28)式更具一般性的表达式,即(44)式。因此,本文的结果不仅涵盖了Levi-Civita符号(张量)主要性质,而且几乎囊括了(推广的)Kronecker符号的所有经常用到的重要性质。
通过多次应用反对称化操作来获取n维时空或空间中含(n+1)个完全反对称指标的零值量,可从而借此以实现指标的轮换。这一操作技巧在广义相对论及其相关扩展理论,如超引力与弦理论等中有极其广泛的应用空间。因此,期望本文的反对称化操作能为这些领域的应用提供一些启示。

