First-principles calculations of the structural, elastic, and ther modynamic properties of M2C(M=V, Nb, Ta)
LUO Yan, LIU Ke , LEI Jin-Qiao, CHEN Hong-Jie , ZHOU Xiao-Lin
(1.College of Physics and Electronic Engineering, Sichuan Normal University, Chengdu 610101, China;2. Department of Basic Medicine, North Sichuan Medical College, Nanchong, Sichuan 637000, China 3.School of Micro-Electronics and Solid-State Electronics, University of Electronic Science and Technology, Chengdu 610054, China)
Abstract: An investigation on electronic structure, elastic and thermodynamic properties of M2C (M=V, Nb, Ta) (space group: pbcn, No: 60 ) under high pressure has been conducted using first principles calculations based on density functional theory. This theory is on the basis of the plane wave that is set to be implemented in the CASTEP code. Firstly, the lattice constants calculated in this article are in good agreement with the available experimental results and the previous theoretical data. Secondly, we calculated the partial and total densities of state whose results show that these three transition-metal carbides are metallic and the order of metallicity from high to low is: V2C > Nb2C > Ta2C. Thirdly, elastic constants Cij, the aggregate elastic moduli (B, G, E) and the Poisson’s ratio have been investigated under high pressure. The calculated bulk modulus of Ta2C (257 GPa) is the highest among them. On the ground of the elastic stability criteria, it is predicted that these three compounds are mechanically stable within 100 GPa. The calculated B/G ratios indicate that these three compounds possess ductile nature within 100 GPa. Finally, using the quasi-harmonic Debye model, we also investigated the thermodynamic properties of these three compounds.
Key words: M2C; Electronic structure; Elastic properties; Thermodynamic Properties; First principles
1 Introduction
Group IV and V d-transition metal carbides are strongly non-stoichiometric interstitial compounds. Group V metals (V, Nb and Ta) have high hydrogen permeabilites, mechanical strength and hardness. Furthermore, their lower prices and richer natural resources make them have been extensively used as membrane materials and cutting tools[1, 2]. Moreover, they also have been widely applied to the field of catalysis, such as catalytic hydrogenation, decomposition of ammonia, aromatization[3-8]. Up to now, a large number of experiments and theoretical studies had been conducted for M2C (M=V, Nb, Ta) carbides[9-12]. These experiments found that they have at least five structure types: (a) anti-Cd(OH)2or C6, (b) anti-CaCl2, (c) ε-Fe2N, (d) ζ-Fe2N and (e)ξ-Nb2C. At room temperature, the crystal structures of V2C, Nb2C and Ta2C are the type d, e and a, respectively[13, 14].
In the V-C system, according to x-ray diffraction studies of nearly stoichiometric V2C[11-13], at low temperature V2C has two ordered phases: a hexagonal β′ phase (space group Pm31 ) stable on the carbon-deficient conditions and an orthorhombic α phase (space group Pbcn) stable below 1100-1600 K. In previous literature[13, 14], the calculations were performed to investigate the crystal structure, phase stability, electronic structure, and mechanical properties of V2C. Chongetal. investigated the elastic module of V2C under 0 GPa using the first principles method[15], and the results show that theα-V2C is stable and can be synthesized under high pressure. In the binary Nb-C system, Nb2C exists in three polymorphic forms: γ-Nb2C phase with a disordered hexagonal structure (forms above 2500 ℃ ), β-Nb2C with an ordered trigonal structure (exists in the temperature range of 1200~2500 ℃), and α-Nb2C with orthorhombic structure (exists at 1200 ℃ and below). Rudyetal. proved that the low-temperatureα-modification of Nb2C has a structure similar to that ofξ-Fe2N by the experiment[6]. Vishwanadh et al. performed a systematic study on the structural, elastic, and electronic properties of stable and metastable niobium carbides by nano-indentation and first principles calculations. It came to the conclusion that many of these carbides are metastable[16, 17]. For the Ta-C system, in early experimental and theoretical studies, Ta2C has four possible structures, i.e.C6-Ta2C[18],ε-Ta2C[11], Mo2C (Pbcn)[8]andL′3- Ta2C[19]. The calculated formation energy of the Ta2C in Mo2C (Pbcn) phase has negative value ( Eform= -1.827 eV) which clearly indicates that it is thermodynamically stable.
With the great breakthrough of high-pressure test means,many new phenomena have been found in the study of the properties of condensed matter under high pressure[20-23]. But, there is still a lack of research on the mechanical properties, electronic structure and the elastic properties of M2C (M=V, Nb, Ta) under high pressure. In this research, the first principles calculations are employed to systematically investigate those aspects of M2C (the space group: Pbcn, No: 60 ) under high pressure. And then, the quasi-harmonic Debye approximation is used to calculate the heat capacity and thermal expansion coefficient of M2C in the range of 0-1200 K.
2 Computational method
In this study, the first principles calculations are performed in the CASTEP code, and the ultrasoft pseudo potential was employed to describe the interaction between ions and electrons[24-27]. The Ceperly-Alder functional form of the Perdew-Burke-Ernzerhof (PBE) functional form of generalized gradient approximation (GGA) were used to describe the exchange and correlation functional[28], wave functions of valence electronics expand in the form of plane wave basis sets. The electronic configurations were taken as 3d34s2for Vanadium, 4d45s1for Niobium, 5d45s1for Tantalum and 2s22p2for Carbon. The energy cutoff was set to 400 eV. The Brillouin zone sampling was performed according to Monkhorst Pack grids and the Gamma centeredk-point,mesh parameters were 6×5×6. The crystal structures of M2C are prepared from references[8, 11, 16].
3 Results and discussion
3.1 Equilibrium structure and mechanical properties
We first optimize structure parameters of M2C under zero pressure. The crystal structure and the total energy per formula unit as a functions of volume for M2C are shown in Fig. 1. The data of this study, previous experimental and theoretical values are listed in Table 1. It is seen that the results are in agreement with the experimental data and the data from other theoretical calculations, indicating that the choice of pseudopotential and approximation is reasonable, which gives us confidence to investigate the elastic and thermodynamic properties of M2C under high pressure.

Fig. 1 The total energy per formula unit as a functions of volume for (a)V2C, (b)Nb2C, (c)Ta2C, and inset shows these crystals structure
Table 1 The calculated equilibrium lattice parametersa,b,c(in Å), equilibrium volumeV(in Å3), bulk modulusB(in GPa).

CarbidesSpacegroupLatticeparametersabcVBRefV2Cpbcn4.551715.73395.03125131.311243.30Thisstudy4.5705.7425.026131.887Exp.[12]4.3056.0315.080131.894244.17Cal.[8,15]4.5405.7765.031240Cal.[13]4.4955.6284.929279Cal.[15]4.5515.7355.032242Exp.[14]Nb2Cpbcn4.972086.242995.43099168.581238.21Thisstudy5.256.0625.311169.025252.92Cal.[8]4.9566.245.4000166.997Exp.[16]4.9726.2555.437Exp.[17]Ta2Cpbcn4.997546.383615.500270175.471257.45Thisstudy5.0726.0895.32164.300303.57Cal.[8]
The pressure dependence of the normalized parametersa/a0,b/b0,c/c0, and volumeV/V0as a function of pressure are shown in Fig. 2. Obviously, the volume shrinks constantly with pressure increasing. The compression ratios of M2C range from 0.931 (for V2C), 0.930 (for Nb2C), 0.935 (for Ta2C) at 20 GPa to 0.779 (for V2C), 0.772 (for Nb2C), 0.790 (for Ta2C) at 100 GPa respectively, decreasing by about 16.32% (for V2C), 16.99% (for Nb2C), and 15.51% (for Ta2C), so the rate of change follows the order of Nb2C > V2C > Ta2C, which reveals that Nb2C is weakest resistant to compression, while Ta2C is the most resistant to compression.

Fig. 2 The normalized parameters a/a0, b/b0, c/c0, and normalized volume V/V0 as functions of pressure for M2C (M=V, Nb, Ta ).

Fig. 3 Calculated band structures and PDOS for V2C (a, d), Nb2C (b, e) and for Ta2C (c, f) at 0 GPa.
3.2 Electronic structure of M2C
Based on the optimized structure, we calculated the electronic structure of M2C. Fig. 3(a-b) displays the electronic band structure of three M2C ( M=V, Nb, Ta ) compounds along the high symmetry directions. It can be seen that all of them exhibit metallic behavior. To understand the electronic nature of these three compounds at a fundamental level, their total and partial densities of states (PDOS) were calculated at zero pressure as presented in Fig. 3(d-f). It is clear that all the compounds exhibit metallic character because of the appearance of finite value ofEFat the Fermi level and the absence of an energy gap near the Fermi level. For the three compounds, the trends of PDOS are similar, and the PDOS can be divided into three main regions: the lowest band (from -15 eV to -10.5 eV) having mainly C-s character and being well separated from other states, the second region (from -7.5 eV to -2.5 eV) containing C-p and M-d hybridized states, the third region, the Fermi level between two peaks mostly occupied by M-d state until 5 eV. The value of DOS at Fermi energy gets lower as the mass of M atomic number increases in the M2C compounds.
3.3 Elastic properties
Elastic constants of solid compounds are important because of their close relations with various fundamental physical properties, such as elastic modulus, Debye temperature and phonon spectra. It is well known that in the elastic range, the orthorhombic crystal has nine independent elastic coefficientsC11,C22,C33,C44,C55,C66,C12,C13,C23. The necessary conditions for mechanical stability are given by the following equation[29].
C11>0,C22>0,C33>0,
C44>0,C55>0,C66>0,
[(C11+C22+C33+2(+C12+C12+C23))]>0
(C11+C22-2C12)>0, (C11+C33-2C13)>0,
(C22+C33-2C23)>0.
(1)
C11,C22,C33characterize the bond strength along the <001>, <010>, <100> direction respectively. The calculations results suggest that the elastic constants of all the three M2C compounds satisfy all of these conditions. For an orthorhombic crystal, we can calculate the value of bulk modulusB, shear modulusGand Young’s modulusEdirectly within these elastic constants based on the Voigt-Reuss-Hill method (VRH)the formulas as follows[30-32].
3(C44+C55+C66)-(C12+C13+C23)]
BR=Δ[C11(C22+C33-2C23+C22(C33-2C13)-
2C33C12+C12(2C23-C12)+C13(2C12-C13)+
C23(2C13-C23]-1
GR=15{4[C11(C22+C33+C23)+C22(C33+
C13)+C33C12-C12(C23+C12)-C13(C12+
C13)-C23(C13+C23)]/Δ+
3[(1/C44)+(1/C55)+(1/C66)]}-1
(2)
where
Δ=C13(C12C23-C13C22)+C23(C12C13-
(3)
While calculating the bulk modulusBand shear modulusG, Voigt approximation and Reuss approximation correspond to the theoretical maximum value and minimum value respectively. Hill approximation is the arithmetic mean values of the Voigt and Reuss approximation. The formulas are as follows[33, 34]:
(4)
(5)
The Young modulusEis obtained by the following formulas:
(6)
Then, the mean Poisson’ ratio(ν) is thus given by:
(7)
Table 2 lists the calculated elastic constants of M2C under zero pressure, the results of V2C have a good agreement with previous theoretical calculation, which means that the present calculation approach is reliable. However, there is no report about the elastic constants for Nb2Cand Ta2C. The elastic constants of M2C under the pressure ranging from 0 to 100 GPa are also calculated and the results are shown in
Fig. 4. It can be seen that theC11、C22andC33values are larger than the other constants and the elastic constants increase as the pressure increases, which means that increasing pressure can improve the materials hardness and Ta2C have the largest elastic constants.
Table 2 Elastic coefficientsCijbulk modulusB, shear modulusG, the Young modulusE(in GPa),B/G, and the Poisson ratiovof M2C at 0 GPa.

C11C22C33C44C55C66C12C13C23BGB/GERefV2C4053814161091291371821231882431212.01311Thisstudy400383414110130135182120189242121311GGA.[14]4524504931221431612071462052791402.00359LDA.[15]393381410107125131181122189240118303GGA.[13]Nb2C3963854121001251271751321672381182.02303ThisstudyTa2C4373914161161351401861631882571252.07322Thisstudy

Fig. 4 Pressure dependence of the elastic coefficients (Cij) of M2C
Additionally,based on the parameter B/G, we can evaluate the ductility of materials. A substance is brittle ifB/G< 1.75, otherwise the material behaves in a ductile manner[27, 35, 36]. The calculated results are also listed in Table 2, indicating that the M2C could be classified as ductile material at zero pressure. Then, the effect of pressure on the B/G ratios has been investigated and the results are shown in Fig. 5(a), It can be seen that the B/G ratios increase as the pressure increases. Furthermore, the Poisson’s ratios of three M2C (M=V, Nb and Ta) compounds are illustrated in Fig. 5(b). It can be seen that the Poisson’s ratios increase with external pressure increasing in the range of 0.25~0.5 within 100 GPa, indicating that the interatomic forces are central forces.
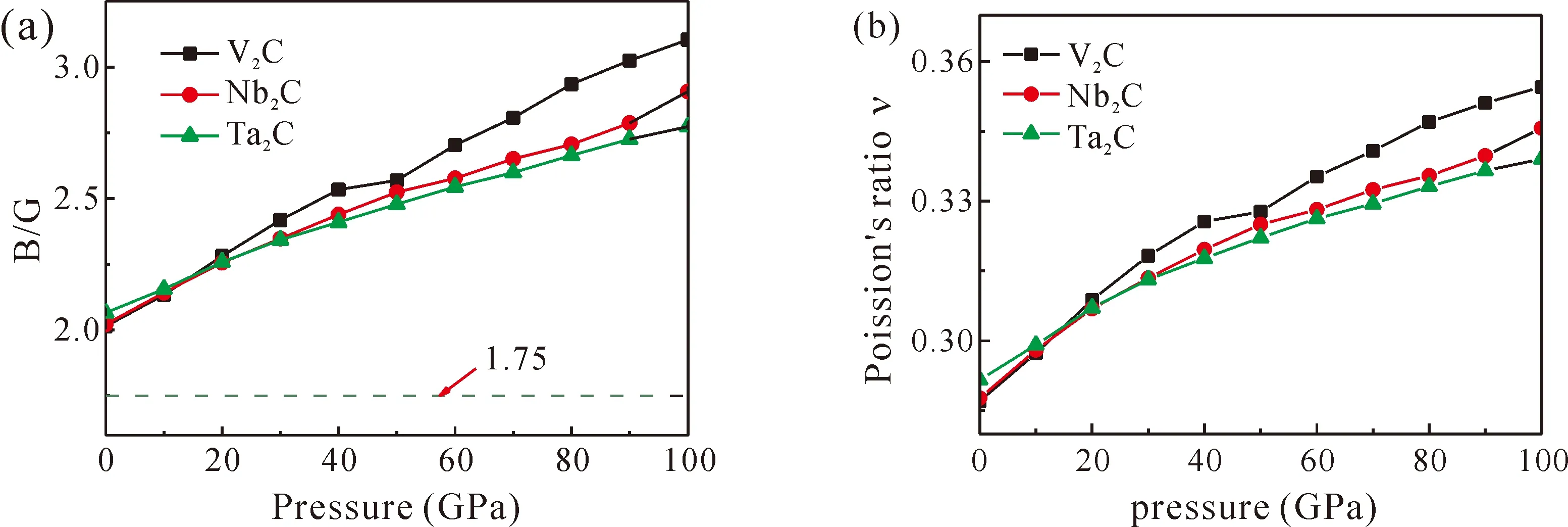
Fig. 5 Pressure dependence of (a) B/G and (b) poission’s ratio ν of M2C.
3.4 Thermodynamic Properties
The theoretical methodof the Debye model has been reported in details in Refs[37-40]. Based on the Debye quasi-harmonic approximation, the thermodynamic quantities of M2C at different temperature (0, 500, 1000, 1500, 2000, and 2500 K) and pressure were obtained.
In Table 3, we listed the Debye temperatureΘD, entropySand Grüneisen parameter γ of M2C at different temperature and pressure. For the three compounds, on one hand, under the given pressure, the Debye temperature gradually decreases, while Grüneisen parameter γ increases as the temperature increases. On the other hand, under the given temperature, the Debye temperature of M2C increases with external pressure increasing. And it can be found that under the given temperature and pressure, the values of Debye temperatureΘDdecrease with the atomic number increasing.
Table 3 Values of the Debye temperature Θ(K), entropy S(J/molK) and Grüneisen parameter γ of M2C (M=V, Nb, Ta).

Table 3 Values of the Debye temperature Θ(K), entropy S(J/molK) and Grüneisen parameter γ of M2C (M=V, Nb, Ta).
P/GPa02050100T/KΘSγΘSγΘSγΘSγV2C0950.2301.9151080.7401.7621234.7501.6151431.3701.452500947.1658.2801.9191078.5950.291.7641233.3142.501.6161430.4734.511.4531000940.98105.961.9281073.9096.551.7691230.4687.011.6191427.9876.801.455Nb2C0746.1401.879846.9301.680962.6501.5001107.8801.323500743.9474.021.884845.4165.561.683961.6657.331.5021107.2548.721.3241000740.10123.311.893842.59113.901.688959.65104.551.5041105.8594.481.325Ta2C0564.3801.991641.8201.866734.9201.747856.6301.609500562.4293.291.995640.3184.251.868733.8374.951.749855.8064.771.6101000559.42143.822.001637.90134.171.872731.94124.121.751854.29112.911.611

Fig. 7 The specific heat capacity CV versus temperature and pressure.
We also calculated theother thermodynamic properties of M2C, such as the thermal expansionαare shown in Fig. 6. It shows that for a given pressure, at low temperature region (T< 400 K), the thermal expansion coefficientαof M2C increases rapidly with temperature increasing, while the value gradually increases slowly at higher temperature region ( 400~1200 K). For the given temperature,αdecreases as pressure increases. When the temperature is lower, the influence of pressure on thermal expansionαis relatively smaller.
The specific heat capacityCVof M2C as functions of temperature are shown in Fig. 7. It can be seen that the specific heat capacityCVdepends on both temperature and pressure. At a given temperature,CVdecreases slowly with the pressure increasing. At a given pressure, the specific heat capacityCVof M2C increases rapidly with the temperature increasing. However, at higher temperature, the anharmonic effect onCVis suppressed, andCVis very close to the Dulong-Pettit limit: 3nNAkBis 74.83 J·mol-1·K-1, wheren=3 for M2C,NArepresents the Avogadro constant andkBis Boltzmann constant.
4 Conclusions
In summary, we have investigated the structural, elastic and thermodynamic properties of the M2C by the first principles calculations. Their optimized lattice parameters are in excellent agreement with other available experimental and theoretical values. Through the analysis of the electronic structure, it found that all of them exhibit metallic behaviors, and the value of DOS decreases at Fermi energy with M atomic number increasing in the M2C compounds. The calculated elastic properties for these compounds indicated that Nb2C has the smallest constants, indicating that the Nb2C is less resistant to deformation than V2C and Ta2C, theC11、C22andC33values of M2C are larger than the other constants. The B/G and Poisson’s ratios under high pressure were also calculated and the results suggest that three M2C compounds could be classified as ductile material. The values of Debye temperatureΘDwill decrease when the atomic number or the external pressure increases. Finally, the thermal properties of M2C are obtained using the Debye quasi-harmonic approximation. Unfortunately, there are no previous calculations and experimental values for any comparison.

