自适应高斯—厄米特滤波器

范 炜，李 勇，林 波

0 引 言

滤波问题是从带有噪声的观测数据中，对系统的状态或者参数进行估计的问题.上世纪六十年代，Kalman和Bucy等人提出的Kalman滤波方法(KF)，为滤波理论和技术的发展做出了重要的贡献.标准的卡尔曼滤波器是在精确已知的线性模型的基础上，得到的线性最小方差估计.由于该方法是线性系统假设下的最优估计，使得其在非线性系统的滤波应用中出现了诸多问题.上世纪七十年代，扩展卡尔曼滤波器(EKF)被提出，目前该方法已经成为非线性系统中广泛应用的滤波估计方法.然而EKF三十多年的应用，也暴露出该算法存在难以实现(必须将非线性系统线性化，计算Jacobian矩阵等)、参数难以调节(参数的不合适往往导致滤波发散)，对更新时间段内系统必须近似线性等诸多问题[1].针对这些问题，近十几年产生并逐步发展了一类基于sigma点的非线性滤波方法(主要包括无迹滤波器[1-2](UKF)、插值滤波器[3](DDF)和高斯—厄米特滤波器[4-5](GHF)等).不同于EKF将非线性系统局部线性化的策略，该类方法通过sigma点的选取和变换来近似状态的均值和方差的非线性变换.对于非线性系统，该类算法体现了较高的滤波精度和较好的滤波稳定性[2].基于高斯—厄米特积分公式(Gaussian-Hermite rule)的GHF是其中一种新型的非线性滤波方法，该方法利用一组带权值的高斯积分点通过非线性映射，对映射后的高斯点进行统计，来得到系统状态的均值和方差的估计.在非高斯分布下，该方法的精度与UKF同阶，而在高斯分布的假设下，该方法的精度则更高，同时可以方便地通过增加高斯点个数来提高滤波器的精度，因此近年来获得较为广泛的应用[6-7].

卡尔曼滤波和基于sigma点的非线性滤波方法均需要较为精确的系统和测量的模型.当系统参数和噪声统计特性存在偏差时，将会导致滤波精度的下降，有时甚至引起滤波的发散.为了解决这一问题，在线估计系统参数、噪声统计特性和修正滤波增益的自适应滤波技术被广泛的研究，主要包括贝叶斯法、极大似然法、相关法和协方差匹配法等.其中较有代表性的是Sage和Husa提出的Sage-Husa自适应滤波方法[8]，该方法利用噪声统计特性的次优极大验后估计(即Sage-Husa噪声估计器)，结合卡尔曼滤波器，得到适用于带平稳噪声的线性系统的自适应滤波算法.我国学者邓自立在其基础上，通过引入遗忘因子，得到改进的适用于带时变噪声特性的线性系统的自适应滤波器[9].Sage-Husa自适应滤波器因其计算简单，原理清晰，而被广泛地研究和应用.

本文将Sage-Husa噪声估计器推广到非线性系统，得到更为一般的递推估计形式，结合高斯—厄米特非线性滤波方法，提出一种新型的自适应高斯—厄米特滤波器(AGHF).仿真表明，对于存在一类未知噪声(系统噪声或测量噪声)参数的非线性系统，与EKF、GHF和自适应扩展卡尔曼滤波器(AEKF)相比，AGHF可显著提高噪声统计特性和系统状态的估计精度，是一种非线性系统高精度滤波器.

1 高斯—厄米特滤波器

1.1 线性最小方差递推滤波框架

一般用估计误差的方差大小来衡量估计精度，所以我们自然希望得到最小方差估计.然而，要得到最小方差估计，需要知道被估计量的验后概率密度函数，而在实际问题中，验后概率密度函数往往无法用有限个参数来完全表示，这给应用带来了较大的困难.而线性最小方差递推滤波框架只需要利用状态的前二阶矩的统计信息，使该框架的应用较为简单，计算量也相对较小，适合在线递推计算，于是在实际应用中被广泛地采用.基于该框架的滤波算法主要包括：KF、EKF、UKF、DDF和GHF等.

线性最小方差估计和误差方差阵的递推方程如下[10]:

(1)

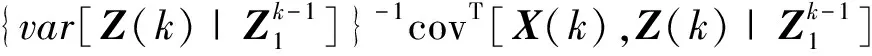
(2)

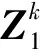
由式(1)、(2)可知，只需计算X和Z的前二阶矩就可以实现状态X的线性最小方差的递推估计.对于线性系统来说，已知前一时刻状态的前二阶矩，可以精确且容易地得到状态通过系统方程和测量方程的前二阶矩，此时得到的滤波方法就是卡尔曼滤波算法.而对于非线性系统要得到前二阶矩的变换则十分困难，一般情况下得不到解析解.针对这一问题，基于sigma点的非线性滤波技术(如UKF, DDF和GHF等)通过采样sigma点，对每个sigma点进行非线性变换，最后进行加权统计的方法，估计非线性变换后的前二阶矩.该类算法不需要计算系统的Jacobian矩阵，使得设计相对简单，同时可实现较高的滤波精度.

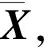
(3)

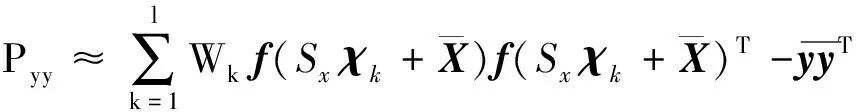
(4)

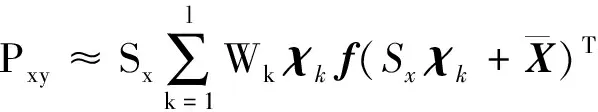
(5)

其中，χk和Wk为高斯分布下的高斯型求积节点和系数，l为求积节点个数.

1.2 高斯—厄米特滤波器

考虑如下非线性离散系统

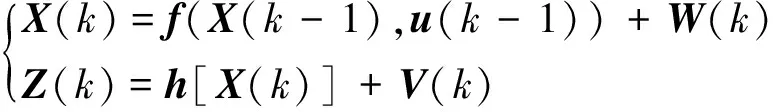
(6)

其中，u(k)为输入项，状态矢量X(k)为满足系统约束且服从高斯分布的随机矢量，其与噪声互不相关，W(k)和V(k)为零均值高斯分布的噪声序列，且有

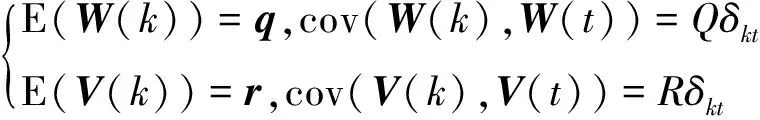
(7)

δkj为克罗内克尔函数.

将利用高斯—厄米特求积公式得到的前二阶矩式(3)～(5)代入式(1)、(2)，可得高斯—厄米特滤波器[4]：

1) 状态初始化：

2) 预测过程

Pxx(k-1|k-1)=S(k-1)S(k-1)T

(8)

i={1,2,…l}.

(9)

f[ζi(k-1|k-1),u(k-1)]+q

(10)

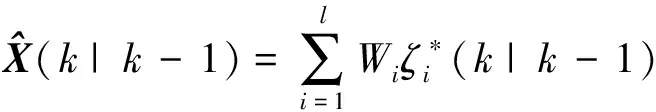
(11)

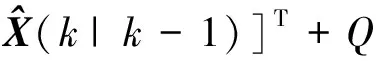
(12)

3) 更新过程

Pxx(k|k-1)=S(k|k-1)S(k|k-1)T

(13)

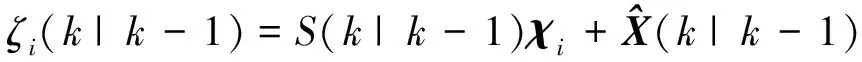
(14)

Zi(k|k-1)=h[ζi(k|k-1)]+r

(15)

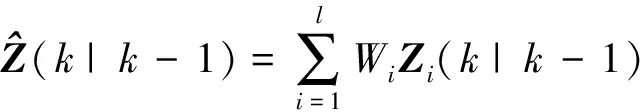
(16)

Pzz(k|k-1)=

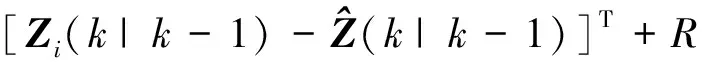
(17)

Pxz(k|k-1)=

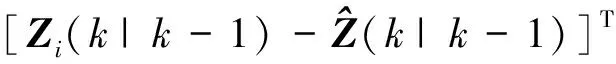
(18)

(19)

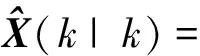
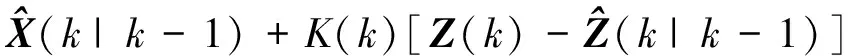
(20)

Pxx(k|k)=

Pxx(k|k-1)-K(k)Pzz(k|k-1)KT(k)

(21)

2 非线性系统Sage-Husa噪声估计器

将Sage-Husa次优极大验后噪声估计器推广到非线性系统，考虑式(6)所示的非线性离散随机系统则有噪声估计器为

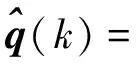
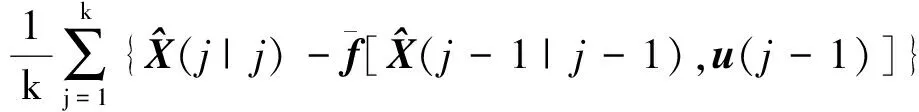
(22)

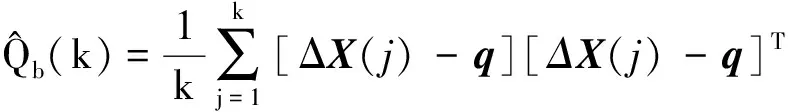
(23)

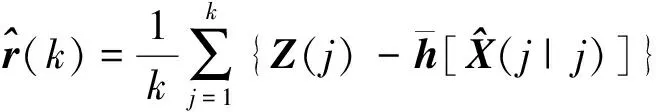
(24)

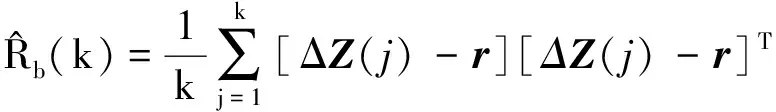
(25)

其中

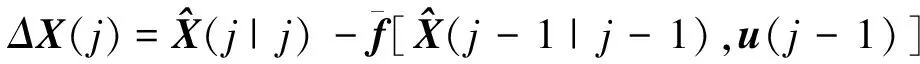
(26)

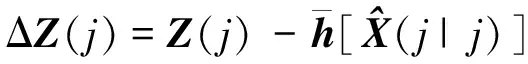
(27)

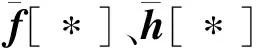
记新息

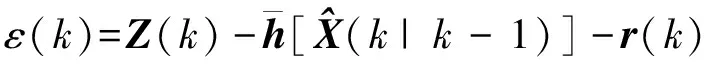
(28)

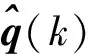
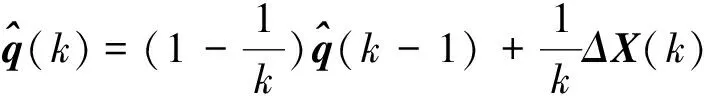
(29)

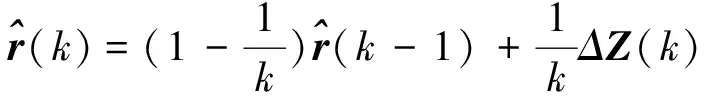
(30)

E(ε(k)εT(k))

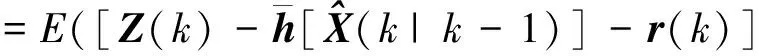
=Phh(k|k-1)+R

(31)

其中

Phh(k|k-1)=

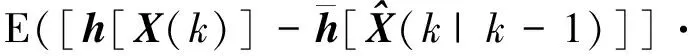
(32)

则

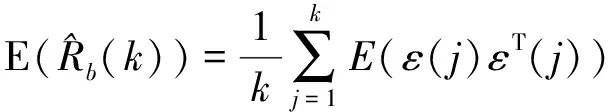
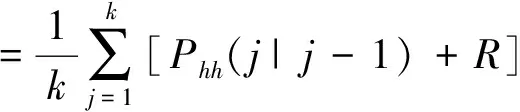
(33)

故式(25)是有偏估计，而R的无偏估计为

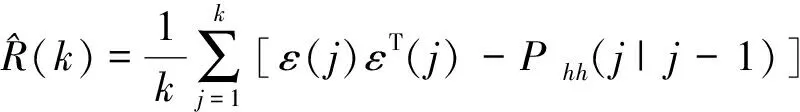
(34)

又因为

Pzz(k|k-1)=Phh(k|k-1)+R

(35)

可得R的无偏递推估计为

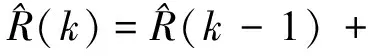
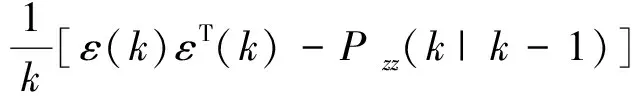
(36)

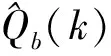
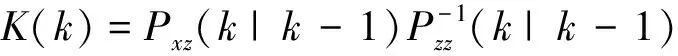
(37)

则有

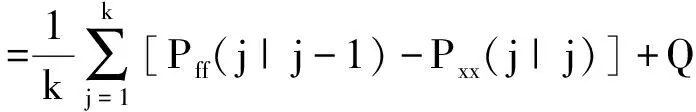
(38)

其中

Pff(j|j-1)=

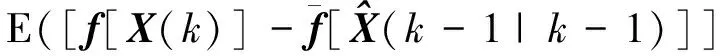
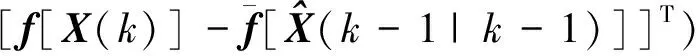
(39)

故式(23)是有偏估计，而Q无偏估计为

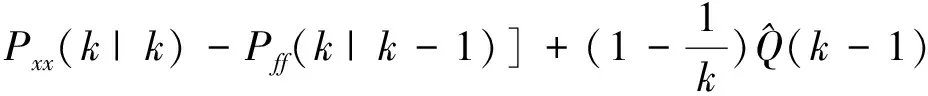
(40)

又因为

Pxx(k|k)=Pff(k|k-1)+Q(k-1)-

K(k)Pzz(k|k-1)KT(k)

(41)

则Q的无偏递推估计为

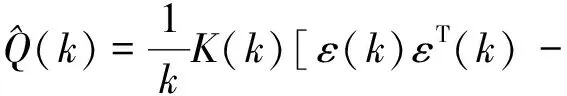
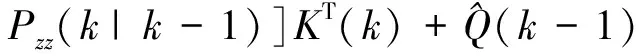
(42)

针对带时变统计特性噪声的非线性系统，通过引入遗忘因子，可以得到非线性时变噪声无偏递推估计器为

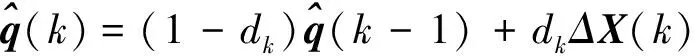
(43)

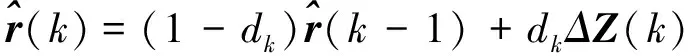
(44)

Pzz(k|k-1)]KT(k)

(45)

-Pzz(k|k-1)]

(46)

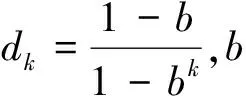
本节将Sage-Husa噪声估计器推广到非线性系统，得到了适用于非线性系统的更为一般的Sage-Husa噪声估计器，该估计器不需要对非线性系统线性化，不需要计算Jacobian矩阵.这使得该方法在避免线性化误差的同时，便于使用sigma点采样技术来实现噪声统计特性的高精度估计.

3 自适应高斯—厄米特滤波器

将高斯点采样技术应用于非线性时变噪声递推估计器，同时结合高斯—厄米特滤波器(GHF)，则可得到自适应高斯—厄米特滤波器(AGHF).考虑式(6)所示的非线性离散系统，则AGHF的实现算法如下：

1) 状态和参数初始化：

2) 高斯点采样

Pxx(k-1|k-1)=S(k-1)S(k-1)T

(47)

ζi(k-1|k-1)=

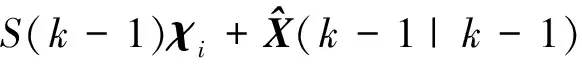
(48)

其中i={1,2,…l}.

3) 状态预测

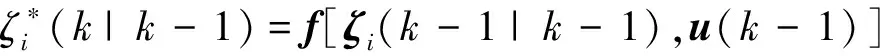
(49)

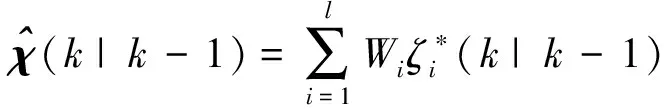
(50)

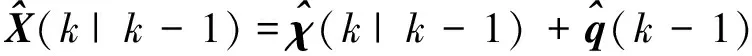
(51)

Pff(k|k-1)=

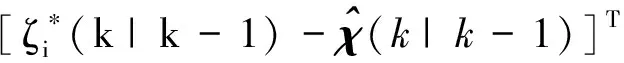
(52)

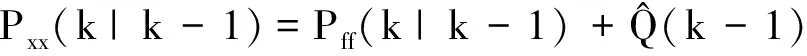
(53)

4) 高斯点再采样

Pxx(k|k-1)=S(k|k-1)S(k|k-1)T

(54)

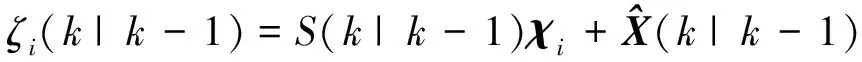
(55)

5) 输出预测与测量噪声参数更新

yi(k|k-1)=h[ζi(k|k-1)]

(56)

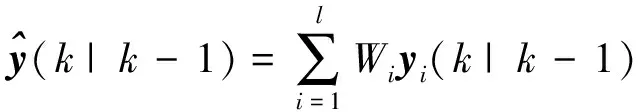
(57)

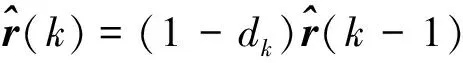
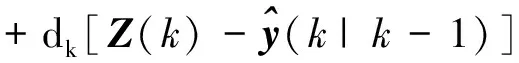
(58)

Phh(k|k-1)=

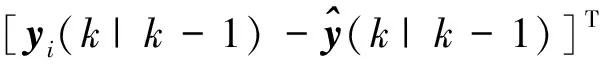
(59)

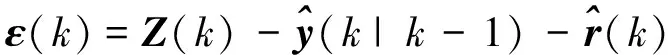
(60)

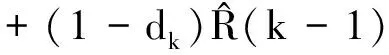
(61)

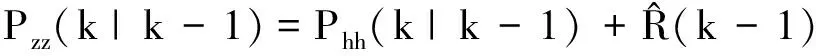
(62)

6) 状态与系统噪声参数更新

Pxz(k|k-1)=

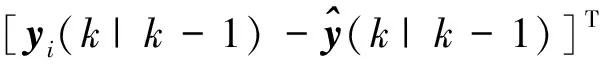
(63)

(64)

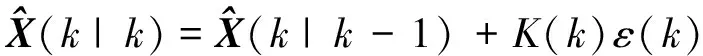
(65)

Pxx(k|k)=Pxx(k|k-1)-

K(k)Pzz(k|k-1)KT(k)

(66)

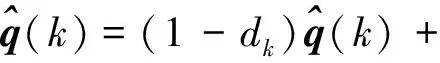
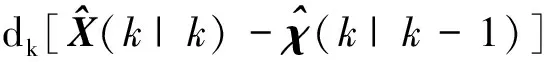
(67)

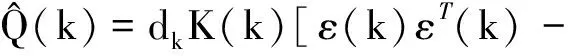
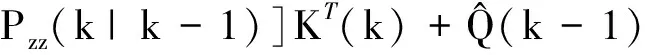
(68)

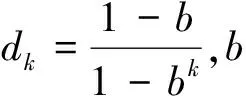
4 仿真实例

考虑如下非线性系统：

其中，w(k)和v(k)是相互独立的噪声序列，q=E(w(k))=2，Q=cov(w(k),w(j))=8δkj，r=E(v(k))=3，R=cov(v(k),v(j))=0.02δkj.

仿真条件：

a) 实例1：v(k)的初始估计为：均值r0=0、方差R0=2.实例2：w(k)的初始估计均值q0=0，Q0=2.

b) 高斯型积分滤波器求积节点个数l=7，仿真步数为3 000.

c) 使用滤波器估计误差绝对值的均值来衡量滤波器估计的精度.

1) 系统噪声统计特性参数已知，测量噪声统计特性参数未知

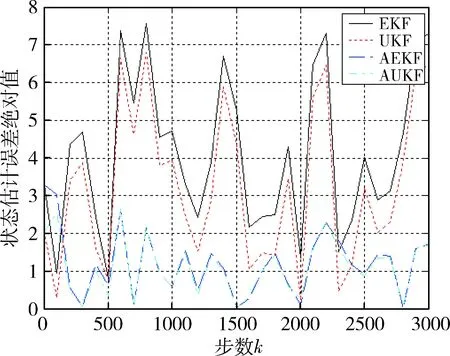
图1 状态估计误差曲线Fig.1 State estimation error

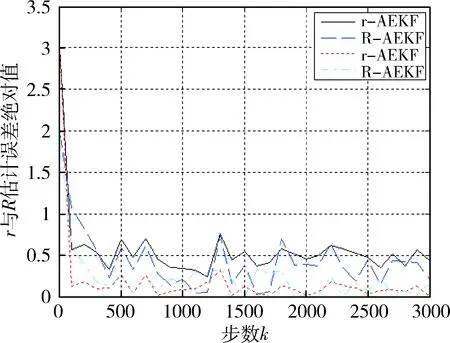
图2 测量噪声统计特性参数估计误差曲线Fig.2 Observational noise statistics estimation errors

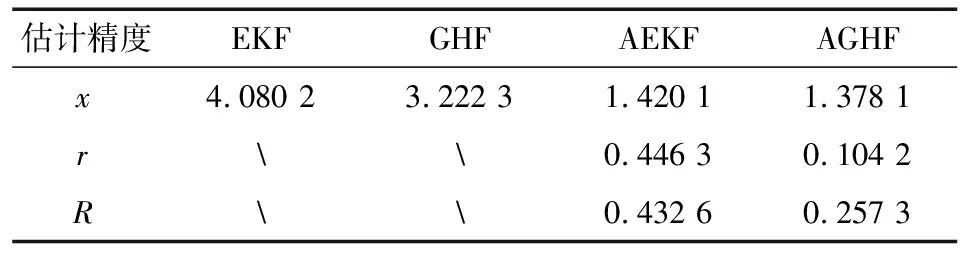
表1 滤波器估计精度比较Tab.1 Comparison of estimation accuracy

2) 系统噪声统计特性参数未知，测量噪声统计特性参数已知

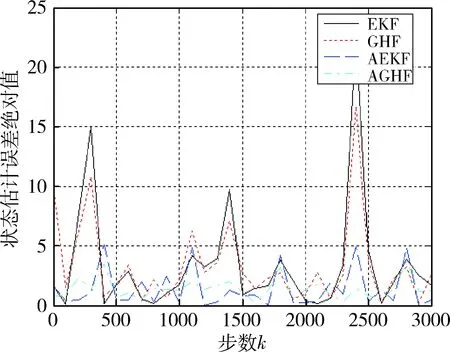
图3 状态估计误差曲线Fig.3 State estimation errors

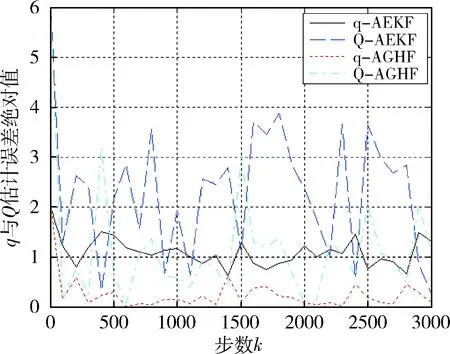
图4 系统噪声统计特性参数估计误差曲线Fig.4 System noise statistics estimation errors

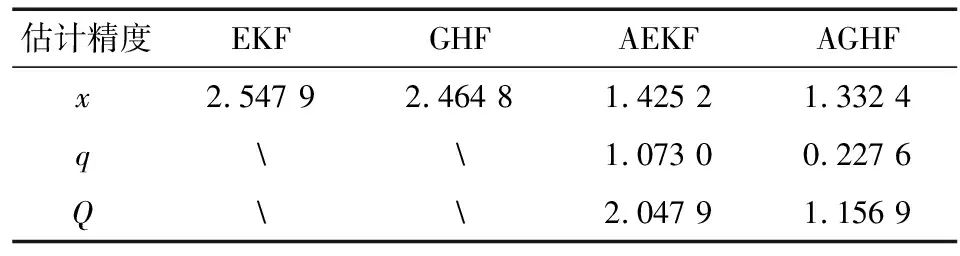
表2 滤波器估计精度比较Tab.2 Comparison of estimation accuracy

对于非线性系统的噪声统计特性参数估计，通过仿真实例可以看出，当系统只存在一类噪声(系统噪声或测量噪声)统计特性参数未知时，AGHF对噪声统计特性参数的估计精度，较使用AEKF的估计有明显地提高，对系统和测量偏差有较强的估计能力.同时必须指出的是，当系统和测量噪声统计特性参数同时未知时，Sage-Husa噪声估计器无法从输出中区分Q和R的影响，故不能对两者同时进行估计.因此，基于Sage-Husa噪声估计器的自适应滤波器(AEKF、AGHF)适用于只存在一类噪声统计特性参数未知的系统.

对于噪声统计特性参数未知的非线性系统的状态估计，通过本节的仿真实例可以看出，当系统噪声统计特性参数未知时，使用自适应滤波器(AEKF或AGHF)较不对噪声统计特性参数进行估计的EKF和GHF，对系统状态的估计精度有显著地提高.与AEKF相比，AGHF由于采用了非线性Sage-Husa噪声估计器和高斯点采样技术，使得在较大地提高噪声统计特性参数的估计精度的同时，对系统状态的估计精度也有明显的改善.

5 结 论

本文将Sage-Husa噪声估计器推广到非线性系统，得到更为一般的Sage-Husa噪声估计的递推形式，同时将推广的噪声估计器与高斯—厄米特滤波器相融合，得到一种新型的自适应非线性滤波器——自适应高斯—厄米特滤波器(AGHF).对于非线性系统的状态和噪声统计特性参数估计，该滤波器采用高斯点采样技术，而不需要对非线性系统进行线性化，从而可得到较高的滤波精度.通过仿真表明，对于一类噪声(系统噪声或测量噪声)统计特性参数未知的非线性系统，AGHF较EKF、GHF和AEKF，估计性能均有明显地改善，能够实现较高精度的统计特性参数和状态估计.同时必须看到对于多维系统，AGHF与 GHF一样，需要的积分节点较多，计算量较大.如何在保持高精度的前提下，减少AGHF的计算量是一个今后值得研究的课题.