浅议初等数学与高等数学有效衔接的路径

姚中华　林鑫　齐贵美

摘  要：对初等数学与高等数学建立有效的路径衔接，是保障学生能够尽快适应高等数学学习的有效手段。通过对数学思想的分析，文章从数形结合的思想、化归与转化的思想、分类讨论的思想、特殊与一般的思想、极限的思想五个路径，给出初等数学与高等数学的有效衔接的具体措施，旨在帮助实现学生由初等数学过渡到高等数学的无缝衔接。

关键词：数学思想  高等数学  初等数学  有效衔接  路径

中图分类号：G642         文献标识码：A            文章编号：1672-1578（2020）02-0014-02

1   引言

高等数学是大学理工类、经管类专业重要的基础课，是一门抽象性高、逻辑性强、应用性广的学科。由于其主要研究对象是无穷和非匀变量，而学生往往以做题为学习的中心环节，忽略了对数学思想和方法的分析总结，从而难以适应高等数学的学习。本文从数学思想的角度出发，分析初等数学和高等数学的教学内容，从而给出从初等数学到高等数学的有效衔接路径。

2   数形结合的思想

学生在中学数学的学习中，能够熟练地利用图形推导平方差公式和完全平方公式、借助数轴和文氏图进行集合的运算、结合函数图像探究函数的性质、通过图解法求解简单的线性规划问题等等;而在高等数学的学习中，学生往往容易忽略从几何的角度理解概念和定理。从数形结合的角度看，高等数学中几乎每一个概念和定理都有对应的几何解释，这些几何解释可以帮助学生理解抽象的知识点。例如，学习一元函数在某点处极限存在的充要条件时，如果结合一正一反两个图形案例来理解这个定理，就会起到事半功倍的效果;类似地，对于函数间断点的学习，可以结合函数的图象，从几何的角度去理解不同类型的间断点，从而正确掌握相应的概念。

3   化归与转化的思想

化归与转化就是将复杂的、待解决或未解决的、不熟悉的问题转化为简单的、已解决或容易解决的、熟悉的问题。在初等数学学习中，学生已经熟练地掌握了将分式方程、二次方程和多元方程转化为整式方程、一次方程和一元方程这些化归与转化的技巧。

在高等数学洛必达法则的学习中，对于两种基本类型的不定式极限，可利用洛必达法则求解;对于其他类型的不定式极限，如幂指函数的极限，则需通过适当的变形转化才能求解。此外，对于幂指函数的求导，既可以用对数求导法转化为隐函数的导数问题，也可以设出合适的中间变量转化为多元复合函数的全导数问题。

4   分类讨论的思想

分类讨论不仅是一种数学思想，更是一种逻辑方法。在初等数学的学习中，学生最乐于使用分类讨论的方法解决数学问题，分类讨论思想在各省的高考试题中也往往占据重要地位。

在高等数学的学习中，分类讨论也是无处不在。例如，不同于数列的极限，函数的极限可以根据自变量是趋于定点还是趋于无穷大而分为两大类，在此基础上，再通过定义单侧极限的概念，进一步将其分为六种形式。对于有理分式函数极限的求解，如果能正确理解函数极限的两大分类，就能快速掌握因式分解消除零因子和同除最高次幂这两种方法的应用范围，进一步，对于自变量趋于无穷时有理分式函数的极限，对分子和分母最高次幂的大小进行分类讨论，可以得到更一般的结论。再如，对于一元函数的间断点，利用左右极限的存在性可将其分为两类，对于第一类间断点，再根据左右极限是否相等又可进一步分类，通过对间断点的分类，可以更好地掌握函数间断点的概念，理解函数连续与间断的本质。

5   特殊与一般的思想

在数学的学习中，很多公式、定理的学习都是通过特殊开始的，从特殊到一般。在初等数学勾股定理的学习中，从毕达哥拉斯地板砖的引入，对等腰直角三角形这一特殊情形进行探究，再引发对一般直角三角形的探讨;在高等数学微分中值定理的学习中，首先引入罗尔定理，然后通过取消定理中两个端点函数值相等的特殊条件，就可以引入更一般的拉格朗日中值定理。

有时，数学的学习也可以从一般情况入手，从一般到特殊，或者说逆向地从特殊到一般。在初等数学中，学生先是认识了一般的四边形，然后转到特殊的四边形——平行四边形，对于平行四边形再从特殊的角度入手，进而认识了矩形、菱形和正方形;在高等数学平面及其方程的学习中，可以在认识平面方程的一般式之后，进一步讨论方程中系数出现零的特殊情况，从而学习了过原点的平面方程、平行于坐标轴的平面方程和平行于坐标面的平面方程。

此外，如果把数列看做特殊的函数，在极限章节的学习中，可先由特殊到一般，从数列极限的概念入手，再学习函数极限的概念，在系统学习函数极限的计算方法之后，再由一般到特殊，回过头来掌握数列极限的计算方法。

6   極限的思想

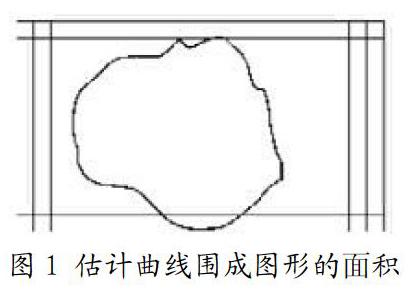
高等数学是一门以极限为基础的学科，处处渗透着极限思想，作为极限存在准则之一的夹逼准则也是求极限的一个重要方法。尽管初等数学课程中并没有直接讲授极限的知识，但在义务教育数学课程标准（2011年版）中却有着这样一道例题：图1中每个小正方形的面积为1个面积单位，试估计曲线所围图形的面积[1]。

如果数出图形内包含的完整的小正方形的个数，就可以估计图形的面积，且估算值比实际面积要小;在此基础上，再加上图形边缘接触到的小正方形的面积，也可以估计图形的面积，且估算值比实际面积要大，实际面积在两者之间。如果要得到更精确的面积值，则应该将正方形网格加密，把所有小正方形分成更小的正方形，这里不仅体现着极限的思想和夹逼准则的应用，同时也蕴含着有限差分算法中网格加密的策略。

7   结语

尽管高等数学与初等数学在内容与深度这两方面差异很大，但是两者所体现的数学思想却是一脉相承的。从数学思想的角度给出从初等数学到高等数学的有效衔接路径，可以使学生进一步深刻认识到这些数学思想，从而增强学习信心，提高学习兴趣，顺利地实现从中学数学到大学数学的过渡。

参考文献：

[1] 中华人民共和国教育部.义务教育数学课程标准[M].北京：北京师范大学出版社， 2011：91-92.

作者简介：姚中华（1993-），男，山东青岛人，助教，研究方向：数学教学、计算数学。