Φ-τ-可补子群对p-超可解性的刻画

施智杰， 毛月梅

山西大同大学数学与统计学院， 山西 大同 037009

0 引言

Skiba A N和郭文彬教授在文献[1]中介绍了子群算子的概念，并列举了它在子群的广义拟正规性和可补性中的一些应用，比如文献[2]提出的S-拟正规子群，文献[3]介绍的SΦ-可补子群以及文献[4]给出的S-半置换子群等各种子群的应用.另外，文献[1]和文献[5]还给出了关于有限群结构一些新的研究方法，利用这些新的手段统一和发展了许多已有的广义拟正规子群，并产生了一系列新的成果.从这些成果中我们可以看出子群算子的性质能更深入地揭示子群性质和群结构的联系.文献[6]利用子群算子并结合SΦ-可补子群的定义，给出了Φ-τ-可补子群这一新的概念，通过讨论子群的Φ-τ-可补性给出p-幂零群一些新的成果.本文在此基础上继续研究子群的Φ-τ-可补性，主要通过讨论群G的准素数子群的Φ-τ-可补性给出p-超可解群一些新的刻画.本文中所讨论的群均是有限群，符号Up指所有p-超可解群组成的群类.未交待的概念和符号参见文献[7,8].以下我们将介绍本文中用到的一些概念.

定义2 子群算子τ称为

(1) 商群遗传的：对于任意群G，如果H∈τ(G)是一个p-子群且N是G的正规子群,那么HN/N∈τ(G/N)；

(2)子群遗传的：对于任意群G，如果H∈τ(G)是一个p-子群且H≤E≤G，那么H∈τ(E)；

(3)正则(拟正则的)：对于任意群G，如果H∈τ(G)是一个p-子群且N是G的一个极小正规子群(交换的极小正规子群)，那么|G：NG(H∩N)|是p的方幂.

(4)Φ-正则(Φ-拟正则)：对于任意的本原群G，如果H∈τ(G)是一个p-子群且N是G的一个极小正规子群(交换的极小正规子群)，那么|G:NG(H∩N)|是p的方幂.

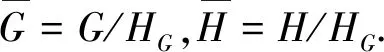
1 预备知识

以下将介绍本文用到的一些引理.

引理1[6，引理2.1]设H是G的一个p-子群且τ是一个商群遗传的子群算子.假定H在G中是Φ-τ-可补的.

(1)如果N是G的正规子群满足N≤H或(|H|,|N|)=1,那么HN/N在G/N中是Φ-τ-可补的.

(2)如果τ是子群遗传的并且满足H≤K≤G，那么H在K中是Φ-τ-可补的.

引理2[9，引理2.16]设F是一个包含所有超可解群的非空饱和群系.设N是G的正规子群且满足G/N∈F，如果N是循环的，那么G∈F.

引理3[8，第IX章，定理3.3]设P是G的一个Sylowp-子群，N是G的正规子群.如果N∩P≤Φ(P)，那么N是p-幂零群.

引理4[1，引理4.4]设F是一个包含群系，P是G的正规p-子群，C是P的Thompson临界子群.如果C≤ZF(G)，那么P≤ZF(G).

引理5[10，引理2.10]设C是非平凡p-群P的Thompson临界子群.

(1)如果p是奇素数，那么Ω1(C)的方次数为p.

(2)如果P是一个非交换2-子群，那么Ω1(C)的方次数为2.

(3)如果p=2，那么Ω2(C)的方次数至多为4.

2 主要结论

定理1 设p是|G|的一个素因子，P是G的一个Sylowp-子群.假定τ是一个Φ-正则子商群遗传的子群算子，并设G的每个包含于P的τ-子群都次正规嵌入于G.如果P的每个极大子群在G中是Φ-τ-可补的，那么G是p-超可解的.

证明 假设定理的结论不正确，对|G|用极小阶反例.

(1)Op′(G)=1

假设Op′(G)≠1，由引理1和定理的假设知G/Op′(G)满足定理假设.因此G/Op′(G)是p-超可解的，并由此得G是p-超可解的，矛盾.所以Op′(G)=1.

(2)如果P≤K≤G，那么K是p-超可解的.

由引理1知P的每个极大子群在K中是Φ-τ-可补的，那么由G的极小性知K是p-超可解的.

(3)G有一个唯一极小正规子群N满足G/N是p-超可解的，G=NM并且MG=1,其中M是G的一个极大子群.

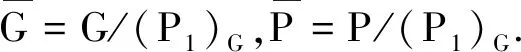
(4)Op(G)=1.

假设Op(G)≠1,那么由(3)知N≤Op(G).因此由(3)易得N=Op(G)=CG(N)且G=N×|M.从而G是p-可解的.令Mp是M的一个Sylowp-子群满足P=NMp,设N1是N的一个极大子群满足N1在P中正规，那么P1=N1Mp是P的一个极大子群且P=NP1. 如果(P1)G≠1，那么由(3)知N≤P1，并因此有P=P1，矛盾.因此(P1)G=1,所以由定理假设G有一个次正规子群T和一个包含于P1的τ-子群S满足G=P1T和P1∩T≤SΦ(P1).因为τ是一个Φ-正则商群遗传的子群算子，所以由(3)知|G:NG(S∩N)|是p的方幂.若S∩N≠1，那么N≤(S∩N)G=(S∩N)P≤P1，这是不可能的.因此S∩N=1.假设S≠1.由于S在G中是次正规嵌入的，所以存在G的一个次正规子群H使得S是H的Sylowp-子群.令L是G的包含于H的极小次正规子群.因为Op′(L)在G中是次正规的，所以由(1)知Op′(L)=1.又因为L是p-可解的,所以L=OP(L)≤OP(G)=N，从而有L∩S≤L∩N=1,这显然是不可能的,因此S=1.从而得P1∩T≤Φ(P1).又因为T是G的次正规子群且|G∶T|为p的方幂,所以由(3)知N≤Op(G)≤T,从而有P1∩N≤Φ(P1).所以P1=P1∩NMp=Mp(P1∩N)=Mp,并由此得N1=P1∩N=Mp∩N=1，从而知|N|=p.那么由(3)及引理2知G是p-超可解的，与假设矛盾.因此Op(G)=1.

(5)N∩P真包含于P

假设N∩P=P，那么P≤N.如果N

(6)最后的矛盾

由(5)知P有一个极大子群P1满足N∩P≤P1. 显然有(P1)G=1.所以由定理假设知G有一个次正规子群T和一个包含于P1的τ-子群S满足G=P1T且P1∩T≤SΦ(P1).我们将证明S=1.假设S≠1.因为τ是Φ-正则商群遗传的子群算子，所以|G∶NG(S∩N)|是p的方幂.如果S∩N≠1，那么N≤(S∩N)G=(S∩N)P≤P1,矛盾.因此S∩N=1.利用类似于(3)的讨论，我们可以设S是G的一个次正规子群H的Sylowp-子群，并设L是G的包含于H的一个极小次正规子群.由(1)和(3)知L是一个非交换单群，于是易得L∩N=1或者L≤N.如果L∩N=1，那么由(2)知L≅LN/N≤G/N是p-超可解的,这是不可能的.因此L≤N，从而推得S∩L≤S∩N=1，即L是一个p′-群，故L=1，但这是不可能的.因此S=1.又因为N≤T，所以N∩P≤N∩P1≤Φ(P1)，那么由引理3知N是p-幂零的，这矛盾于(1)和(4).定理得证.

推论1 假定τ是一个Φ-正则商群遗传的子群算子.如果G的每个非循环Sylowp-子群P的每个极大子群在G中是Φ-τ-可补的，并且G的每个包含于P的τ-子群都在G中是次正规嵌入的，那么G是超可解的.

证明 由定理1知这是显然的.

命题1 假定τ是一个拟正则商群遗传的子群算子，P是G的正规子群p-子群.如果P的每个极小子群或4阶循环子群(当P是一个非交换2-群)在G中是Φ-τ-可补的，那么P≤ZU(G).

证明 假定结论不正确，对(G,P)用极小阶反例.首先证明G有包含于P的唯一极小正规子群N满足P/N是G的主因子.设P/N是G的任一主因子，显然(G,N)满足定理的假设，那么由(G,P)的选择知N≤ZU(G).如果|P/N|=p，那么P/N≤ZU(G/N)，并因此有P≤ZU(G)，矛盾.所以|P/N|>p.现假定P/R是G的另主因子满足N≠R，类似于上面的讨论有R≤ZU(G)，这就推出P=NR≤ZU(G)，这又是一个矛盾，所以N是G的满足P/N的G-主因子的唯一极小正规子群.

设C是P的临界子群，如果Ω(C)1,所以存在包含于P/N∩Z(Gp/N)的一个p阶子群V/N,其中Gp是G的Sylowp-子群.现在令x∈VN，并记H=〈x〉，那么V=HN.由定理假设知|H|=p或4.如果V正规于G，那么有P=V，从而有|P/N|=p,这是不可能的，所以V不正规于G.显然，HG≤VG=N.因此由定理假设知G/HG有一个次正规子群T/HG和一个包含于H/HG的τ-子群S/HG满足G=HT并且H/HG∩T/HG≤S/HGΦ(H/HG).现假定H/HG=S/HG.因为τ是一个拟正则商群遗传的子群算子，所以SN/N是G/N的一个τ-子群，并且|G:NG(V)|=|G:NG(HN)|是p的方幂.从而有V正规于G，这又是一矛盾.因此我们假定H/HG≠S/HG，那么H/HG∩T/HG≤Φ(H/HG).显然H≠HG.因此H∩T≤Φ(H).在这种情况下显然有P∩T

定理2 设p是|G|的一个素因子，Gp是G的一个Sylowp-子群，并且τ是一个Φ-正则商群遗传的子群算子.如果P的每个极小子群或4阶循环子群(当P是一个非交换2-群)在G中是Φ-τ-可补的,那么G是p-超可解的.

证明 设M是G的任一极大子群，那么由引理1易知M满足定理的假设，因此由G的选择知M是p-超可解的，从而知G是一个极小非p-超可解群.所以由文献[11，第VII章，定理6.18]知G有一个正规的p-子群P满足P=GUp，由命题3知P≤ZU(G).因为G/GUp是p-超可解的，所以G是p-超可解，定理得证.