一种基于预处理迭代算法的核磁共振T2谱反演∗

李鹏飞 佟喜峰 游博洋

（东北石油大学计算机与信息技术学院 大庆 163318）

1 引言

在地球物理、遥感技术、工业控制以及信号（图像）处理等众多科学技术领域中，一般都存在反问题的求解问题。这些反问题对应的数学模型很多都是病态线性方程组。

在求解病态线性方程组时，其数值解是不稳定的。由于系数矩阵和右端常数项量大多来源于原始观测资料，而原始资料中存在的观测误差会因系数矩阵的病态性被放大，导致算法的数值解偏离真解而失去意义。以Ax=b方程组为例说明病态系数矩阵对解的误差的放大作用。在其系数矩阵和右端向量存在观测误差时，则变为如下形式：

式（1）有如下估计式成立［1］：

其系数矩阵的谱范数意义下的条件数为2503，属于比较严重的病态程度。精确解为x1=-100，x2=-200。假设系数矩阵存在扰动，则方程组变为

则得到一个截然不同的解：x1=40000，x2=79800。

当病态系数矩阵的条件数很大时，在不对系数矩阵做出预先处理的情况下，就直接使用常规的求解方法得到的数值解误差会非常大甚至无法获得数值解。所以，目前对于病态线性方程组求解一般都围绕先对病态系数矩阵进行改良这种方法开展工作，即先对病态系数矩阵进行预处理，将其改造成良态矩阵后，再进行求解。文献［2］中SSOR-ICCG算法，其迭代过程不影响ICCG算法的收敛性，而且通过SSOR预处理来降低系数矩阵的条件数，从而提高算法的稳定性，加快收敛速度。该算法要求系数矩阵必须对称正定。文献［3～4］中均提到正则化方法求解病态的反问题，方法是对病态矩阵进行正则化改造，使之变为良态，然后用这个正则解作为待求方程的近似解。这类方法中如何确定正则化参数，使正则解更好地逼近原问题的解比较困难。根据原始观测数据中误差水平是否已知，有后验策略和先验策略两种方式来确定正则参数。黄小为［5］认为谱截断的正则化方法甚至比Tikhonov正则化方法更为有效，因此基于截断奇异值分解法［6～10］被越来越多的科研工作者应用在各自领域的反问题求解过程中。此外，人工神经网络和基于进化计算一类的智能优化算法［11～15］也被应用于病态的反问题求解。

本文将病态系数矩阵进行改造，在降低其病态性的同时，构造了一种简单的预处理迭代算法，来求解严重病态的线性方程组。

2 预处理迭代算法设计

设有如下形式线性方程组：

其中，(aij)n×n>0 。，构建对角阵D，并将DX叠加在式（3）两端，得式（4）：

根据式（4）得：

要确保迭代公式（6）有效则必须满足D+DA可逆，以及迭代矩阵(D+DA)-1(D-K)收敛两个条件。由于矩阵D和DA均为元素大于零的对角阵，所以D+DA必可逆。下面对迭代矩阵的收敛性予以证明。

3 迭代矩阵收敛性证明

结论1：设式（3）中系数矩阵A为实正定方阵，则式（6）中迭代矩阵(D+DA)-1(D-K)必收敛。

证明：设λ为系数矩阵A的特征值，λ'为迭代矩阵(D+DA)-1(D-K)的特征值，则对于这两个矩阵有如下等式成立：

对于系数矩阵和迭代矩阵的任意一个特征值λi，，有：

根据所构建的对角阵D可知，式（6）中迭代矩阵严格行对角元素占优，且主对角线元素均大于0，依据文献［16］中定理3的结论：矩阵中任一特征值实部必大于0。则迭代矩阵为正定矩阵，所以>0。又因为A正定，所以λ>0。a>0，d>0iiii（已知），所以<1。由此得出：0<<1，因此迭代矩阵收敛。证毕。

4 预处理迭代算法对比实验测试

4.1 Hilbert病态线性方程组测试

以20阶Hilbert病态线性方程组为测试实例，其中：

Hilbert矩阵元素：

右端向量：

在实际测试过程中，为了验证算法的稳定性，取一组xj=1(j=1，2，…，20)作为真解代入方程组，求得右端向量后，在其基础上添加SNR=50的高斯白噪声。表1中对比了本文中设计的预处理迭代法、Matlab中自带的非负最小二乘法优化函数、遗传算法和雅可比迭代法四种方法求解结果。预处理迭代算法的停止条件为当0.001退出迭代。遗传算法采用了Matlab中自带的遗传算法工具箱，其除了具有简单遗传算法的选择、交叉和变异算子之外，还有精英个体复制策略、迁移策略和惩罚函数等算子，用来提高数值解的精度。

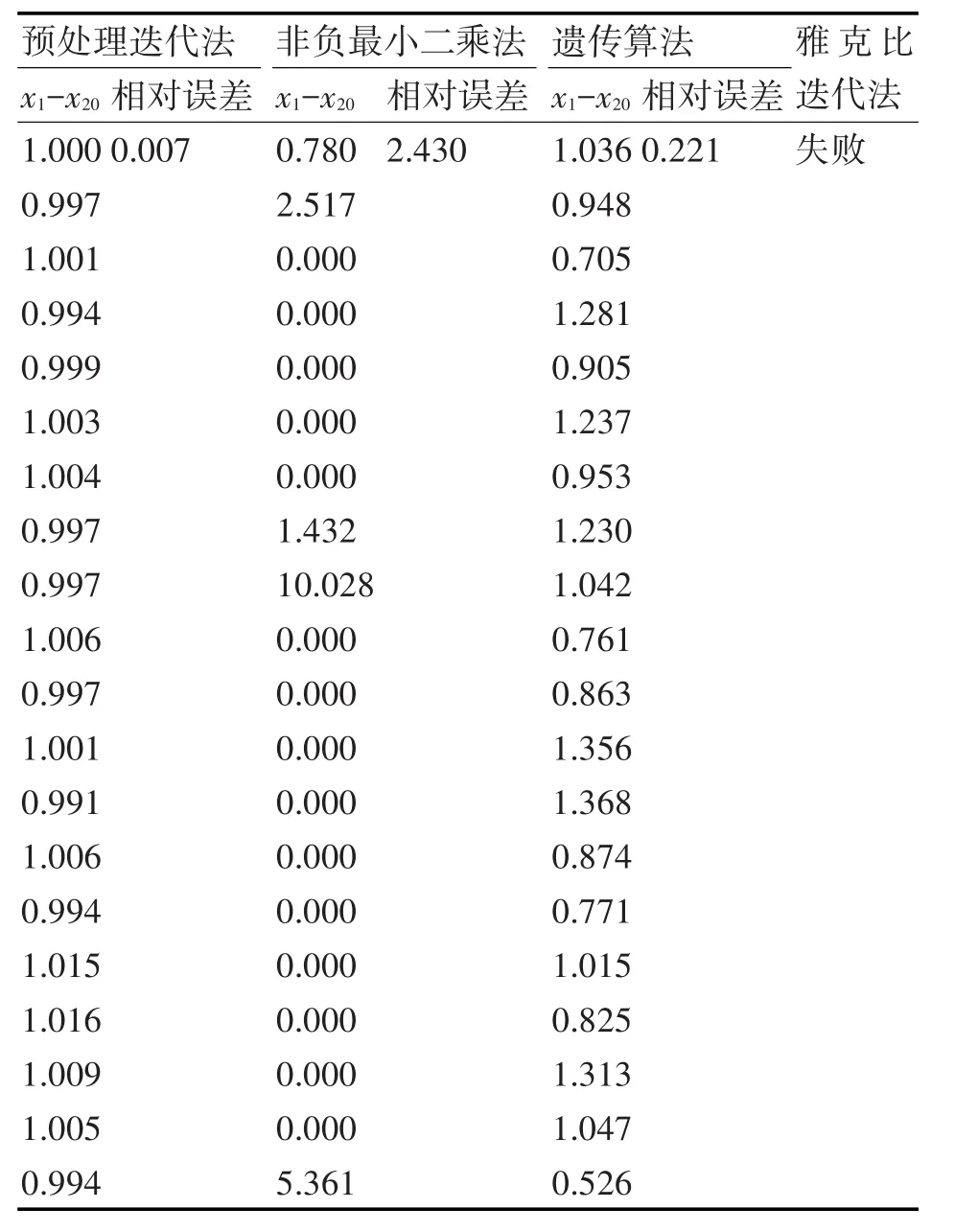
表1 20阶Hilbert病态线性方程组求解对比

4.2 核磁共振T2谱模型反演测试

根据核磁共振测井理论可知，氢原子核系统磁化强度矢量的横向分量是按指数规律衰减的，由CPMG脉冲序列测得的回波串也按指数规律衰减。储层岩石通常存在一个孔隙尺寸分布，并且常常含有多种流体成分，此时孔隙中存在多种弛豫组份，即横向弛豫时间常数（T2）不是单值，而是一个分布，称之为T2谱［17］。由CPMG脉冲序列测量记录的自旋回波串按多指数规律衰减，即各单指数衰减的叠加。回波幅度与横向弛豫分量初始幅度之间满足式（10）关系［17～18］：

式中：bi为CPMG脉冲序列测量记录的第i个回波幅度；Ej为第j个横向弛豫分量的初始幅度（正数）；T2j为第j个横向弛豫分量衰减的时间常数；TE为CPMG脉冲序列测量记录的回波间隔；N为横向弛豫分量的个数；M为回波个数。

T2谱反演就是根据预设的T2值和仪器测得的回波串数据，求解出Ej来拟合测得的回波串数据。这一过程称为解谱或多指数拟合。其实质是求解M个方程，N个未知数的线性方程组。

在实验室以实测的某井岩心回波数据为T2谱反演模型的右端向量，回波间隔表达式取TE=322.65+(i-1)×300，横向弛豫分量的个数取N=128，回波个数取M=2048。某井岩心实验参数表如表2所示。

表2 某井岩心实验参数表

该井岩心数据构成的模型为超定线性方程组，将其左乘系数矩阵的转置矩阵，则原方程组变为其正则方程组。使用预处理迭代算法对其进行反演解谱，并与实验室中英国牛津核磁共振分析仪（MARAN）自带的解谱软件包的解谱结果进行了对比，如图1所示。

图1 预处理迭代法和MARAN解谱对比图

5 结语

在20阶Hilbert病态线性方程组的测试实例中，添加了SNR=50的高斯白噪声。此时，系数矩阵数值是精确的，而右端向量相当于有了扰动δb。经过Matlab中计算，其系数矩阵谱范数意义下的条件数为1.53×1018，已经严重病态。观察表1可以得出：预处理迭代法的相对误差为0.007，精度还是相当高的。遗传算法的某些解偏离精确解比较大，导致相对误差也比较大。而非负最小二乘法的数值解除已经严重失真，失去了意义。对系数矩阵未经处理而直接用雅可比迭代法进行求解，算法失败，这也印证了文中前面所提：如果不对病态矩阵进行预处理而直接使用常规的解法进行求解时通常会失败。求从求解的速度来看，在双核i3-2130，主频3.4GHz，4GB内存的台式机上，预处理迭代法和非负最小二乘法求解时间均为0.01s的数量级，而遗传算法（进化代数2000代，停滞代数50）的求解速度最慢，约为10s数量级。

对于用实验室岩心数据构建的T2谱反演模型，回波间隔和回波幅度均为仪器测定，所以反演模型中系数矩阵和右端向量分别存在扰动δA和δb。根据仪器测定的参数，按照式（10）计算，系数矩阵谱范数意义下的条件数为1.253×1019，病态性比测试实例1更重。将原方程组转换为正则方程组后，系数矩阵病态性会进一步加剧（谱范数意义下的条件数为7.113×1020）。此时，对于任何算法，求出稳定的数值解难度都非常大。预处理迭代算法是在对病态的系数矩阵改造的基础上而构成一个迭代公式，并对其进行求解，所以解的精度和稳定性得到了有效的提高。通过观察图1可以得知预处理迭代算法反演结果与牛津核磁共振分析仪自带的解谱软件的反演结果基本吻合，谱的形状与变化趋势基本一致。因此，与比较昂贵的进口仪器相比，采用预处理迭代算法进行反演，具有更好的性价比。

以上两个测试实例具有较好的代表性，既有理论数据构造的系数矩阵，也有仪器实测的原始数据形成的具有扰动的系数矩阵和右端向量，能够更好地检验算法的数值解稳定性。从解谱结果对比来看，可以得知预处理迭代算法是求解严重病态线性方程组的一种有效算法。