时滞神经网络的改进稳定判据
韩彦武,汤红吉,余跃
(1.南通大学 理学院, 江苏 南通 226019; 2.南通大学 杏林学院, 江苏 南通 226007)
0 引言
神经网络(neural networks, NNs)在很多领域有着广泛的应用。在神经网络中,由于神经元之间通讯时间等因素的存在,不可避免产生时滞现象。时滞的存在将使得系统的性能变差甚至失稳。而稳定是一切系统正常运行的基础,因此,基于Lyapunov稳定性理论,对于时滞神经网络(DNNs)稳定性的研究是近年来的热点问题之一。目前,时滞神经网络稳定性的研究已经有了众多结果[1-10]。通常,采用的方法是通过构造适当的LKF泛函,综合利用各种计算方法和技巧,得出系统保持稳定所允许的最大时滞。得出的最大时滞(AUBD)越大,说明结果的保守性就越小。
文献[5,6]分别利用基于自由矩阵的积分不等式和改进的基于自由矩阵的积分不等式方法,得出了DNNs指数稳定的充分条件。文献[7]利用基于Wirtinger的多积分不等式,对DNNs 进行了稳定性分析。文献[8]通过构造含有三重积分的增广LKF泛函,以线性矩阵不等式的形式给出了DNNs稳定的充分条件。文献[9]利用一般自由权矩阵方法,估计增广LKF泛函导数中的单积分项,得出了保守性较小的DNNs稳定条件。文献[10]在构造LKF泛函时,充分利用了激活函数和时滞的相关信息。注意到文献[5-10]中得出的DNNs稳定充分条件均需要较多的矩阵变量。矩阵变量较多将增加计算的复杂度,而且有时并不能降低结果的保守性。
基于此,笔者研究DNNs的稳定性问题。构造了一个适当的增广Lyapunov-Krasovskii泛函(Lyapunov-Krasovskii functional LKF),估计LKF泛函沿误差系统导数时,综合应用倒凸组合技巧,基于辅助函数的积分不等式,根据激活函数的界,应用较少的矩阵变量,得出DNNs稳定的一个新判据。
1 问题描述
考虑如下的时滞神经网络:
(1)

(2)

(3)
其中,f(x(t))=g((x(t)+y*))-g(y*)。由式(2)可得:
(4)
下面给出本文需要用到的引理。
引理1对于正定对称矩阵M,向量函数ω:[t-d,t]→Rn有定义[11-12],则:
其中:
引理2ξ∈Rn,Φ=ΦT,B∈Rm×n且rank(B) ①ξTΦξ<0,∀Bξ=0,ξ≠0; ② (B⊥)TΦ(B⊥)<0,B⊥是B的右正交补。 为了表示方便,定义如下符号: K2=K1+Θ(K3-K1)=diag(k1,…,kn),Θ=diag(θ1,…,θn),θi∈(0,1), p(t)=d(t)e8+(d-d(t))e9, ((e6-e7)-Kj(e1-e4))TΔi3(Kj+1(e1-e4)-(e6-e7))], d1(t)=d(t),d2(t)=d-d(t),i,j=1,2, Γ=[-A-I000W0W10000]。 定理1对于给定的d,μ,θi∈(0,1), 对角矩阵K1,K3,式(3)是渐近稳定的,若存在对称矩阵P,对称正定矩阵Z,Q,R,S,Ui(i=1,2,3),对角正定矩阵Λ1,Λ2,Δij,i=12,j=1,2,3 及矩阵Mi(i=1,2,3)使得如下的线性矩阵不等式成立。 (5) (6) (7) 证 情形 1。 (8) V(t)=V1(t)+V2(t)+V3(t)+V4(t)+V5(t), 其中: V5(t)=d(t)xT(t)Sx(t), 由引理1得: 若式(7)成立,则V1(t)>0。沿式(3)Vi(t)计算导数如下: xT(t-d)Rx(t-d)=ξT(t)Ξ1ξ(t); 由引理1和引理3可得: 综上可得: 关于V4(t),V5(t)导数的计算,由引理1可得: 由式(4),对于任意的正对角矩阵Δij(i=1,2,j=1,2,3)有如下不等式成立, 2di(t)(f(x(t))-K1x(t))TΔi1(K2x(t)-f(x(t)))≥0; 2di(t)(f(x(t-d(t)))-K1x(t-d(t)))TΔi2(K2x(t-d(t))-f(x(t-d(t))))≥0; 2di(t)((f(x(t))-f(x(t-d(t))))-K1(x(t)-x(t-d(t))))TΔi3(K2(x(t)- x(t-d(t)))-(f(x(t))-f(x(t-d(t)))))≥0; 根据上面的推导可得: 情形 2 (9) 构造如下的LKF泛函: 与情形1类似推导可得: 注定理1给出了DNNs稳定的一个新判据,所需矩阵变量较少,而且通过下面的数例验证,得出的允许时滞范围较大,原因主要表现在以下三个方面: ① 通常在构造LKF泛函时,所有的矩阵都需要是对称正定矩阵[5-10],从而保证了LKF泛函的正定性。在定理1中,矩阵P不需要正定,从而降低了对LKF泛函中矩阵的要求, 这在一定程度上,降低了结果的保守性。 ② 在估计LKF泛函沿式(3)的导数时,定理1中采用了比Wirtinger积分不等式[15]保守性更小的基于辅助函数的积分不等式,这在一定程度上也降低了结果的保守性。 ③ 时滞分解是对时滞系统分析的一种方法,但是通常会引入较多的矩阵变量,增大计算的复杂度[16-17]。在定理1中,笔者针对激活函数的界进行了分解,从证明过程来看,并没有增加矩阵变量的个数。 例1在式(3)中,参数矩阵如下: 取Θ=diag(0.68 0.55),当μ取不同值时,相应的时滞最大范围和决策变量个数如表1所示。 表1 例1中不同μ下的最大允许d 由表1可知,本文定理1中的决策变量的个数远小于文献[5-7]中决策变量的个数,从而在一定程度上降低计算的复杂度,而且,应用定理1得出的最大时滞值大于文献[5-7]中的时滞最大值。 例2在式(3)中,参数矩阵如下: A=diag(1.276 9 0.623 1 0.923 0 0.448 0) K1=diag(0 0 0 0),K3=diag(0.113 7 0.127 9 0.799 4 0.236 8), 取Θ=diag(0.64 0.66 0.67 0.60),当μ取不同值时,相应的时滞最大范围和决策变量个数如表2所示。 表2 例2中不同μ下的最大允许d 由表2可知,针对例2,应用定理1得出的最大时滞范围大于文献[8-10]中的时滞范围,且决策变量的个数远少于文献[8-10]中的决策变量个数,表明定理1的保守性较小。 本文主要研究了时滞神经网络的稳定性问题。与以往文献中时滞分解不同,本文对于激活函数的界进行“分解”,这样不会引入较多的矩阵变量。通过构造增广LKF泛函,不要求所有的矩阵正定,得出时滞神经网络稳定的新的充分条件,并以线性矩阵不等式的形式表示。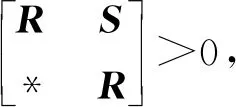
2 主要结论
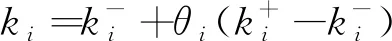
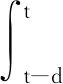
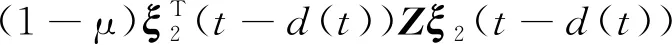

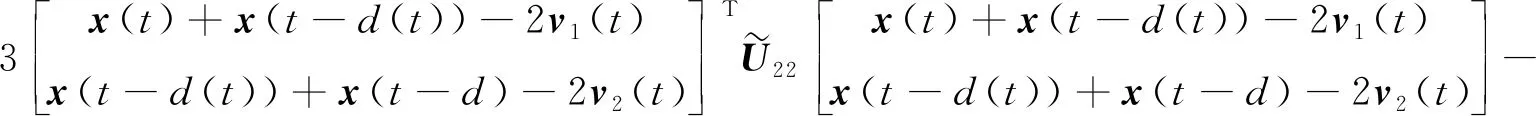
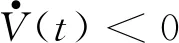
3 数值算例



4 结论

