Positive Solutions for Fractional Differential Equations with Integral and Infinite-Point Boundary Conditions

SHEN Kaiyue(沈凯月),ZHOU Zongfu(周宗福)

(School of Mathematical Science,Anhui University,Hefei 230601,China)

Abstract: We study the positive solutions of a class of fractional differential equations with integral boundary conditions and infinite-point boundary value conditions.By mean of the properties of Green function and the fixed point theorem of cone expansion and compression of norm type,the existence results of the positive solution of the boundary value problem are obtained.Finally,we also give an example to illustrate the applicability of the results.

Key words: Integral boundary condition;Fractional differential equation;Fixed point theorem;Positive solution

1.Introduction

In recent years,the fractional differential equation has been widely used in many fields.Numerous mathematicians has been devoted to the study of it’s related properties[1−4].The solvability analysis of fractional differential equations with boundary conditions has become a hot theme.In this topic,they mainly study the existence or positive solutions of boundary value problems for fractional differential equations[5−10].In this paper,we consider the integral boundary value condition and the infinite point boundary value condition together,and mainly discuss the existence of positive solutions of fractional differential equations for such boundary value problems.

This article deals with integral and infinite-point boundary value problems of the fractional differential equations

Inspired by the above literature,we obtain the existence of positive solutions for fractional differential equations by means of the fixed point theorem of the cone.Compared with the existing literature,this paper has the following two features.First,integral and infinite-point boundary value conditions are considered together in this paper.Second,the aim to this paper is to investigate the existence of positive solutions for boundary value problem (1.1).

In the rest of this paper,the following arrangements have been made.Section 2 is aimed to recall certain basic definitions and lemmas.Section 3 is devoted to gain the main results by virtue of the Guo-Krasnoselskii’s fixed point theorem.Section 4 is intended to illustrate the conclusion with an example.

2.Preliminaries

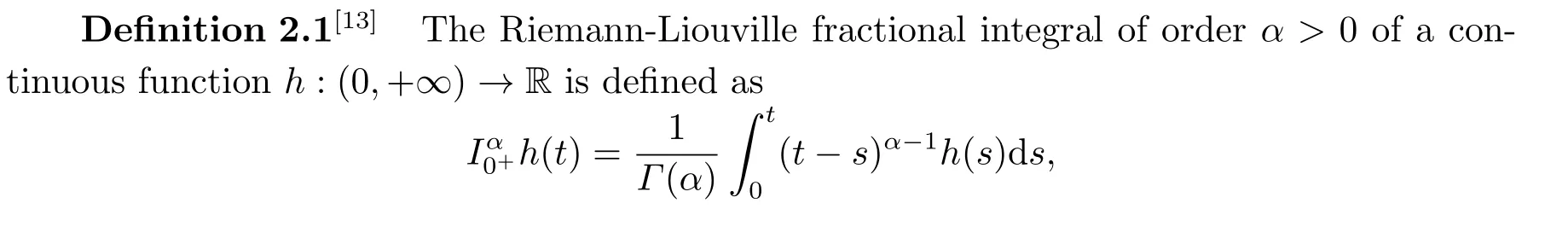
This completes the proof.

Lemma 2.3Suppose thatp(0)>0,and then the functionp(s)>0,s ∈[0,1] andp(s)is nondecreasing on [0,1].

ProofUsing hypothesis made by (1.1),we have

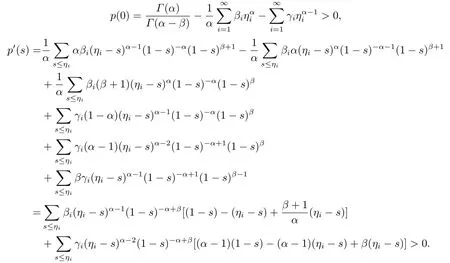
Sop(s) is nondecreasing on [0,1].This completes the proof.

Lemma 2.4The functionG(t,s) defined by (2.2) satisfies the following properties:

Define the operatorTas follows:

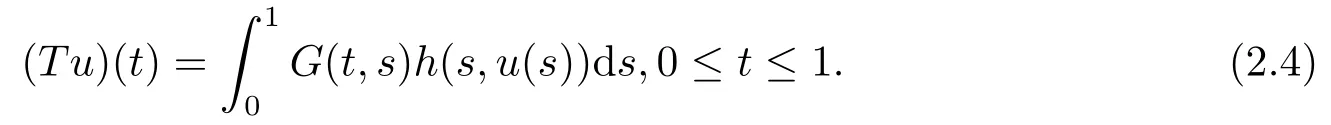
Clearly,T:P →C[0,1].By Lemma 2.2,we get that the fixed point ofTis the solution of problem (1.1).

Lemma 2.5T:P →Pis completely continuous.

ProofFirst,∀u∈P,it follows from the definition ofTand the non-negativity ofG(t,s) andhthat,(Tu)(t)≥0(0≤t ≤1).By Lemma 2.4 and (2.4),we have that

3.Main Results

4.Example

In this section,we will present an example to illustrate our main results.

Example 4.1Consider the following boundary value problem

Therefore the assumptions of Theorem 3.1 are satisfied.Thus Theorem 3.1 ensures that the problem (4.1) has at least one positive solution.