带脉冲毒素的随机三种群模型的动力学分析
高永馨,王娜娜
(中国民航大学理学院,天津 300300)
随着环境污染日益严重,很多学者利用数学模型研究毒素对生物种群的影响[1-2],一般都假设毒素的排放是连续的。然而,在实际情况中毒素是每隔一段时间排放的,这种现象在数学中称为脉冲,故应采用脉冲排放毒素代替连续排放[3]。文献[4]研究了污染环境下脉冲投放毒素对生态系统的影响,且得到当脉冲周期小于某一临界值时,种群就会灭绝,在此过程中,种群数量将逐渐减少,因而受随机因素影响会越来越大,得到的阈值将会和实际情况不符,因而确定性模型难以准确描述系统状态,但随机模型更具有合理性。Bahar 等[5]研究随机时滞Lotka-Volterra 模型,表明白噪声不仅可抑制种群爆炸,同时可使模型的解随机有界。Liu 等[6]讨论了非自治系统在随机扰乱下生存与灭绝的阈值,并研究随机干扰下系统的全局稳定性。随机干扰成为目前的研究热点,但相关研究成果[7-8],主要针对单种群和两种群,对带有脉冲毒素的随机三种群模型研究较少。在真实环境中,三种群及三种群以上的捕食与被捕食关系更为普遍[9],增加研究种群的数目,会相应增加模型的拟合程度和研究难度。因此,考虑带有脉冲毒素的2 食饵1 捕食者的三种群随机模型,通过研究在脉冲毒素和随机干扰下三种群的动力学行为,进而探究在某环境区域内对人类活动所造成影响的最大容纳量,以保证以该地区为主要生存地的种群能持续生存,为后续研究多种群生态模型提供参考。
1 模型构建
依赖于被捕食者和食饵密度的Beddington-DeAngelis 功能反应,在低密度状态下,更加符合实际的生态系统。文献[10]建立带Beddington-DeAngelis 功能性反应的2 食饵1 捕食者确定性模型(系统1),即

其中:初值满足xi(0)>0,i=1,2,y(0)>0;xi(t)为食饵在t 时刻的规模,i=1,2;y(t)为捕食者在t 时刻的规模;r1,r2和r3分别为种群x1(t),x2(t)和y(t)的内禀增长率;aij分别为种群x1(t),x2(t)和y(t)的种内竞争系数,i,j=1,2,3;a12,a21分别为两类食饵种群间的竞争系数别为捕食者y(t)对食饵x1(t)和x2(t)的Beddington-DeAngelis 功能反应,其中,m1,n1为环境容纳度;m2,n2为捕食者对食饵x1(t),x2(t)的饱和作用,m3,n3分别为食饵x1(t)之间、食饵x2(t)之间的相互作用;a13,a23为捕食者y(t)对食饵x1(t),x2(t)的捕获率;a31,a32为捕食者y(t)对食饵x1(t),x2(t)的转化率;所有系数均为正常数。
环境中连续的随机干扰可由白噪声描述,即用ri+αi(B˙i)(t)代替ri。其中,(B1,B2,B3)T是定义在完备概率空间(Ω,F,P)上有相互独立分量的{Ft}t>0可适应的三维标准布朗运动。毒素摄入可用脉冲方程[3-4]表述。因此,将白噪声与脉冲毒素考虑进系统1,可得以下随机三种群模型(系统2)为

其中:初值满足条件xi(0)>0,i=1,2,y(0)>0;σi(t)为噪声强度,i=1,2,3;Ce(t)为环境中毒素的浓度;h为在t 时刻毒素的损失率;τ 为脉冲输入周期;u 是脉冲输入量;li为食饵与捕食者对环境毒素的剂量反应,i =1,2,3。
2 符号表示与相关引理
为了简便,定义符号如下
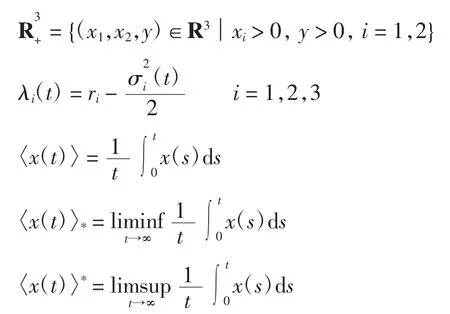
引理1系统2 对于任意给定的初值(x1(0),x2(0),,当t >0,存在唯一的全局正解(x1(t),
证明在t >0 上,对于任意给定的初值μ(0)=ln x1(t),v(0)=ln x2(t)和ω(0)=ln y(0)考虑以下方程
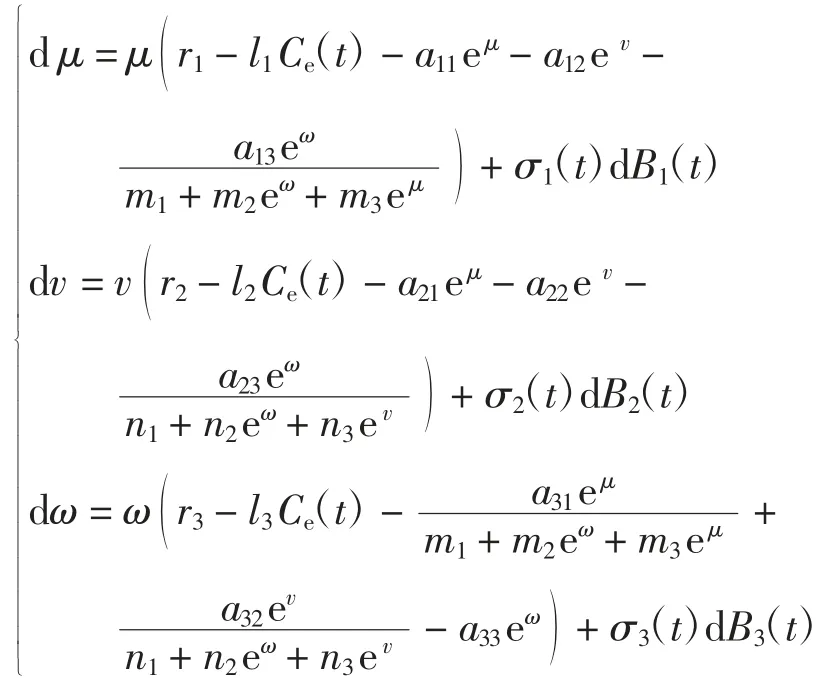
验证上述方程均满足局部Lipschitz 条件,因此,在t >0 上,方程存在唯一局部正解(μ(t),v(t),ω(t)),再利用伊藤公式,x1(t)=eμ(t),x2(t)=ev(t),y(t)=eω(t)是方程满足初值条件x1(0)>0,x2(0)>0 和y(0)>0 的解。
引理2设g(t)∈C(Ω×[0,∞),R+),其中,C(Ω×[0,∞),R+)为定义在Ω×[0,∞)上所有正值函数的集合簇[11]。
Ⅰ)如果存在常数T >0,λ0>0,λ,σi和λi满足
其中,对任意t≥T,则

Ⅱ)如果存在常数T >0,λ0>0,λ,σi和λi满足
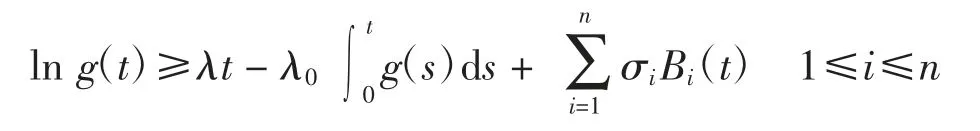
其中,对任意t≥T,则

再考虑系统2 的脉冲毒素因素,将其独立研究并作为系统2 的子系统3,即

引理3系统3 有唯一的τ-周期解Ce*(t),该解是全局自治稳定的[12],即
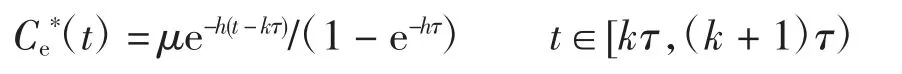
3 灭绝性与持久性
从引理3 可知,系统3 有一全局自治稳定的τ-周期解Ce*(t),因此,系统2 的极限系统(系统4)可表示为

定理1对于系统4,有以下结论。

证明应用伊藤公式到系统4,可得


据以上结论,对定理1 的结论分别证明。
证明Ⅰ利用式(5),可得

再根据式(7)可得到

证明Ⅱ由于通过证明Ⅰ可知x2(t)=0。
再利用式(5),可得

将引理2 中的证明Ⅰ和证明Ⅱ分别作用于式(10)和式(11),可得


将引理2 中的证明Ⅰ作用于式(12),当〈λ3〉*>时,有

从而可知,捕食者y(t)在时间平均意义下有上界。
4 结语
通过建立一类带有脉冲毒素输入的Beddington-DeAngelis 功能性反应的随机三种群模型,分析可发现脉冲毒素的输入与白噪声干扰都对种群的生存起着重要作用。由定理1 可知,是食饵x1(t)与x2(t)的生存阈值,i=1,2,当食饵x1(t)与x2(t)都灭绝且当时,食饵x1(t)在平均意义下强持久。是捕食者y(t)的生存阈值,且当捕食者y(t)会灭绝。此外,当捕食者y(t)在时间平均意义下有上界。
定理的结果客观反映了生态系统中种群稳定性存在的充分条件,利用定理的结论定性和定量估计脉冲毒素输入及随机干扰的情况下种群的生存风险,制定最优策略减少经济损失。

