圆锥曲线中定点分弦成定比问题的探究

广东省广州市番禺区实验中学(511400) 潘神龙

设点P是平面上的一定点(非原点),给定一个实数λ,圆锥曲线C是否有弦MN被点P分成的长度之比恰为λ的两条线段? 如果有,这样的弦有几条? 以往人们认为此类问题解法复杂,且难以用公式表示,较少去研究它.本文系统地研究并解决了此类问题,得到以下结果:弦MN的斜率k与定比λ、µ值之间的关系,定比λ的变化规律,定点P的存在区域……并提供了处理圆锥曲线问题的一种思路.

全文假设:定点P在第一象限,直线MN与圆锥曲线C相交,|MP|≤|NP|,即−1＜λ≤1 且λ0;直线MN绕点P旋转时沿逆时针方向.

1 圆

定理1设圆C:x2+y2=r2,定点P(x0,y0)分斜率为k的弦MN所成比为令µ=x20+y20(µ＞0,µr2),有

证明设弦MN的方程为(t为参数),将其代入圆的方程,整理得

设此方程的两根为t1,t2,分别对应M,N两点,根据t的几何意义,t1=−λt2,所以λ(t1+t2)2+(λ−1)2t1t2=0;由韦达定理,

整理得(Ⅰ).

1.1 定点P 在圆内,0＜µ＜r2

(1)λ=1,弦仅有一条,与OP垂直;(2)1,弦有两条,关于直线OP对称;(3)弦仅有一条,过圆心;(4)−1＜且0,弦不存在.当直线MN绕点P从过圆心旋转至与OP垂直时,λ逐渐变大.

图1

图2

1.2 定点P 在圆外,µ＞r2

(1)−1＜λ弦有两条,关于直线OP对称;(2)弦仅有一条,过圆心;(3)且λ0,弦不存在.当直线MN绕点P从过圆心旋转至趋于与圆相切时,λ逐渐变小.

图3

图4

1.3 推论

推论1当时,(Ⅰ)退化为一次方程,弦有两条,其中一条弦的斜率不存在.

推论2当弦存在时,设若λ＞0,点P满足若λ＜0,点P满足r2＜µ≤由此得到点P的存在区域.

推论3存在以点P为中点的弦的充要条件是0＜µ＜r2.

推论4定比λ是方程1=0 的根.

推论5弦长

证明由t1=−λt2得

2 椭圆

定理2设椭圆定点P(x0,y0)分斜率为k的弦MN所成比为令有

2.1 定点P 在椭圆内,0＜µ＜1.

(1)λ=1,与OP共轭的弦仅有一条(即该弦的中点在线段OP上[1],下同);(2)弦有两条;(3)弦仅有一条,过原点;(4)且0,弦不存在.当直线MN绕点P从过原点旋转至与OP共轭时,λ逐渐变大.

图5

图6

2.2 定点P 在椭圆外,µ＞1.

(1)−1＜λ＜弦有两条;(2)弦仅有一条,过原点;(3)且λ0,弦不存在.当直线MN绕点P从过原点旋转至趋于与椭圆相切时,λ逐渐变小.

图7

图8

2.3 推论

推论1当时,(ⅠⅠ)退化为一次方程,弦有两条,其中一条弦的斜率不存在.

推论2当弦存在时,设λ1,若λ＞0,点P满足若λ＜0,点P满足由此得到点P的存在区域.

推论3存在以点P为中点的弦的充要条件是0＜µ＜1.

推论4定比λ是方程1=0 的根.

推论5弦长

3 双曲线

定理3设双曲线=1(a＞0,b＞0),定点P(x0,y0)分斜率为k的弦MN所成比为令有

3.1 定点P 在双曲线内,µ＞1.

(1)λ=1,弦仅有一条,与OP共轭;(2)且λ0,弦有两条;(3)弦仅有一条,过原点;(4)−1＜λ＜弦不存在.若弦在双曲线的右支之内,当直线MN从与OP共轭旋转至趋于与渐近线平行时,λ逐渐变小;若弦在双曲线的两支之间,当直线MN从过原点旋转至趋于与渐近线平行时,λ逐渐变大.

图9

图10

图11

图12

3.2 定点P 在双曲线与渐近线之间,0＜µ＜1.

(1)−1＜ λ＜且0,弦有两条;(2)弦仅有一条,过原点;(3)＜λ≤1,弦不存在.若弦在双曲线的两支之间,当直线MN从过原点旋转至趋于与渐近线平行时,λ逐渐变大.

图13

图14

3.3 定点P 在渐近线上,µ=0

(1)1,弦仅有一条;(2)λ=1,弦不存在.若弦在双曲线的两支之间,当直线MN从趋于与渐近线平行旋转至趋于与渐近线平行时,λ逐渐变大.

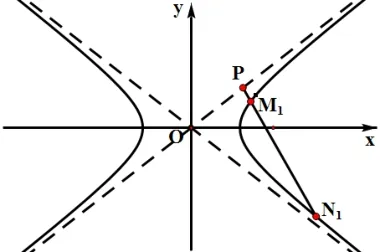
图15

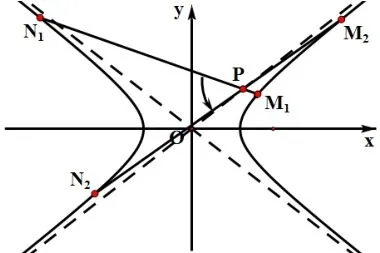
图16

3.4 定点P 在渐近线与y 轴之间,µ＜0.

(1)λ=1,弦仅有一条,与OP共轭;(2)1,弦有两条.若弦在双曲线的右支之内,当直线MN从趋于与双曲线相切旋转至趋于与渐近线平行时,λ逐渐变大(当点P在双曲线外时,本结论都成立);若弦在双曲线的两支之间,当弦从与OP共轭旋转至趋于与渐近线平行时,λ逐渐变小.

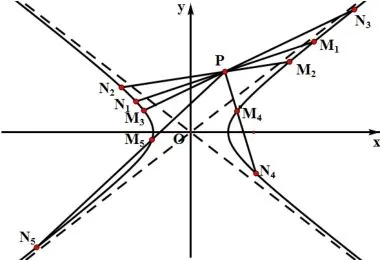
图17

图18

图19

3.5 推论

推论1当时,(ⅠⅠⅠ)退化为一次方程,弦有两条,其中一条弦的斜率不存在.

推论2当弦存在时,设1,(1)若点P在双曲线内,点P满足若点P在双曲线外,点P满足(2)若λ＞0,点P满足µ＞1 或若λ＜0,点P满足µ＜1 或由此得到点P的存在区域.

推论3存在以点P为中点的弦的充要条件是µ＞1 或µ＜0.

推论4定比λ是方程

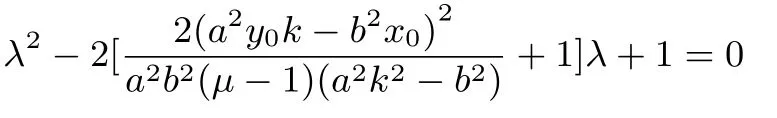
的根.

推论5弦长

4 抛物线

一般抛物线y2=2px(p＞0)在伸缩变换下变成特殊抛物线y′2=x′;我们通过研究后者得到前者的相关结论.

定理4设抛物线C:y2−2px=0(p＞0),定点P(x0,y0)分斜率为k(k≠ 0)的弦MN所成比为令µ=y20−2px0,有

4.1 定点P 在抛物线内,µ＜0.

(1)λ=1,弦仅有一条,与OP共轭;(2)0＜λ＜1,弦有两条;(3)−1＜λ＜0,弦不存在.当直线MN从与OP共轭旋转至趋于与主轴平行时,λ逐渐变小.

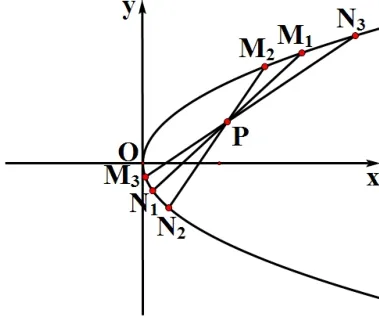
图20

图21

4.2 定点P 在抛物线外,µ＞0.

(1)−1＜λ＜0,弦有两条;(2)0＜λ≤1,弦不存在.当直线MN从趋于与抛物线相切旋转至趋于与主轴平行时,λ逐渐变小.

图22

图23

4.3 推论

推论1当时,(ⅠV)退化为一次方程,弦有两条,其中一条弦的斜率不存在.

推论2存在以点P为中点的弦的充要条件是µ＜0.

推论3定比λ是方程的根.

推论4弦长

5 应用举例

例已知椭圆的方程为P(1,0)为椭圆内一定点,问是否存在过点P的弦MN,使得P分MN所成比例为? 若存在,求出弦MN的长度;若不存在,请说明理由.

解因为所以由定理2,满足条件的弦有两条;计算得弦MN的斜率k是方程的根,所以k=弦长

评注从本例可以看出,定理2 对解决椭圆内的定点分弦成定比问题是快速有效的,此时定点P在x轴上.本例也可采用一般的方法进行求解,但由于比例是个分数,计算量偏大.