离心率问题探究
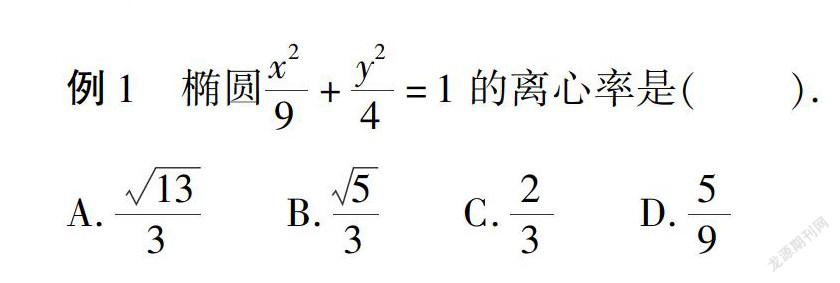

摘 要:离心率问题是高考中考查的一个重点内容,解答离心率问题的过程对学生形成数学核心素养有积极的作用.但学生对这一部分问题往往感觉无从下手,理不出头绪.在大量高考题、模拟题、习题的基础上,笔者把离心率问题涉及的知识点及解决策略进行了分类,抽象出七大模型.学生心中有了模型,解决这类问题也就变得有章可循.
关键词:椭圆离心率;双曲线离心率;关于a,b,c的方程
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2020)10-0012-02
收稿日期:2020-01-05
作者简介:李化周(1981.2-),男,山东省沂水人,本科,中学一级教师,从事高中数学教学研究.
新的课程改革强调将提升学生核心素养作为根本目标.圆锥曲线这部分,包含了直线、圆、椭圆、双曲线与抛物线.通过寻找图形与图形的关系,从图形中抽象出数量关系,总结规律,体验直观想象的过程.或将生活中的数学问题转化为解析几何问题,借助图形使问题得到解决.在这个过程中,可以很好地训练学生的数学抽象与直观想象能力.此外,椭圆、双曲线的离心率是高考的核心考点,出现的频率非常高.离心率问题以中档题为主,它可以与很多知识产生联系,有很多载体,如三角函数、数列、方程等都可以与离心率结合.离心率问题有时灵活性较强,不容易入题;有时运算量大,学生不容易得出正确结论;有时多个知识点相互交融,学生理不出头绪.通过对离心率问题的深入研究,笔者归纳整理了离心率的基本知识,常见的类型及一般的解决策略.让离心率问题有章可循.
一、直接法求离心率
例1 椭圆x29+y24=1的离心率是( ).
A.133 B.53 C.23 D.59
分析 由方程可得,a=3,c2=a2-b2=9-4=5,所以c=5,所以,离心率e=ca=53,选B. 二、利用椭圆、双曲线定义求离心率
例2 已知F1、F2是双曲线E:x2a2-y24=1(a>0,b>0)的左、右焦点,点P在双曲线E上,PF1与x轴垂直,sin∠PF2F1=13,则双曲线E的离心率為( ).
A.2 B.32 C.3 D.2
分析 Rt△PF1F2中,因为sin∠PF2F1=13,设|PF1|=m,则|PF2|=3m,2c=|F1F2|=22m.根据双曲线定义得,2a=2m.故离心率e=2c2a=22m2m=2,选A.
三、利用比例关系求离心率
例3 若双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,线段F1F2被抛物线y2=2bx的焦点F分别为5∶3两段,则此双曲线的离心率为
.
分析 由题意得F(b2,0),c+b2c-b2=53,故c=2b,所以a=3b,故e=ca=2b3b=233.
四、利用三角知识求离心率
例4 已知椭圆x2a2-y24=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若椭圆上存在点P使asin∠PF1F2=csin∠PF2F1,则该椭圆的离心率的取值范围为( ).
A.(0,2-1) B.(22,1) C.(0,22) D.(2-1,1)
分析 根据正弦定理,|PF2|sin∠PF1F2=|PF1|sin∠PF2F1,故|PF1||PF2|=ca,所以,|PF1|=ca|PF2|.根据椭圆定义|PF1|+|PF2|=2a,所以,|PF2|=2a2a+c.因为点P不在长轴上,故a-c<|PF2|0.两边同除以a2得,e2+2e-1>0,解得e<-1-2或e>2-1.因为0 五、利用图形几何性质求离心率
例5 过双曲线x2a2-y2b2=1(b>a>0)的左焦点F(-c,0)作圆x2+y2=a2的切线,切点为E,延长PE交抛物线y2=4cx于点P,O为坐标原点,若OE=12(OF+OP),则双曲线的离心率为( ).
A.3+32 B.1+32 C.52 D.1+52
分析 抛物线的焦点坐标与双曲线右焦点重合为F2(c,0).因为OE=12(OF+OP),所以E是FP的中点.因为O是FF2中点,故OE∥PF2,PF2=2OE=2a.又E是切点,所以OE⊥FP,故PF2⊥FP,PE=OF2-OE2=c2-a2=b,故PF=2b.因为点P在抛物线上,故MP=2a.Rt△PFM中,MF=PF2-MP2=2b2-a2.Rt△PFF2中,S△PFF2=12×2c×2b2-a2=12×2a×2b,所以c2(b2-a2)=a2b2,即c2(c2-2a2)=a2(c2-a2).
整理得c4-3a2c2+a4=0,即e4-3e2+1=0,
解得e2=3+52,所以e=1+52,选D.
在离心率问题的解决过程中,学生经历着图形、向量、三角函数、直线等与离心率之间的联系与融合,由形到数,由数到形,对学生数学素养培育有积极有效的作用.离心率问题虽涉及的情境各不相同,出现的形式异彩纷呈,感觉乱花渐欲迷人眼,其实是花不醉人人自醉.只要我们将遇到的问题模型化,归纳总结其特征及其解决的思路,针对具体问题擦亮眼睛,静下心来,将题中的条件想办法转化为圆锥曲线中a,b,c的关系,离心率问题即可迎刃而解.
参考文献:
[1]吴世朗.全国卷中离心率求值问题的解题策略\[J\].高考,2019(23):41.
[2]曹丽.“一题多变性”变式在高三数学复习中的应用——以“求圆锥曲线的离心率”为例\[J\].中学数学,2019(11):31-32.
[3]玉云化.圆锥曲线离心率范围再探\[J\].中学数学杂志,2010(03):61-62.
[责任编辑:李 璟]

