依形求义，以形表像，形义互补 数形结合在二次函数教学中的实践探究

黄钧军

摘 要：二次函数是初中数学的重要内容，也是中考的一个必考的考点。二次函数对学生的思维和能力要求比较高，它可以和很多知识点综合在一起，既可以横向联系，也可以纵向联系。解决二次函数最重要的思想就是数形结合。运用数形结合可以把复杂的二次函数问题简单化，直观化。用数据来分析函数的图像性质，用图像来分析函数所表达的含义。通过数与形的相互转化，相互表达，加深学生对二次函数知识的理解和掌握，培养学生运用数形结合的数学思想和意识。

关键词：二次函数;数形结合

学生学习二次函数的内容是九年级第一学期，在学习二次函数之前，学生在八年级学习了一次函数和反比例函数，对于函数的概念有了一定的了解，一次函数是刻画匀速变化的模型，反比例函数是刻画定积变化的模型，而二次函数是刻画匀变速变化的模型。学生在学习二次函数的知识过程中，对于二次函数的图像特征把握不清晰，对二次函数的性质掌握不深刻，导致在解决二次函数的问题的时候找不到方法，或者适得其反，在二次函数的问题上花费大量时间而没有结果，对函数的学习也失去了信心，也降低了学习数学的兴趣。本文从二次函数的数和形两方面进行教学实践探究，通过探究二次函数的形状来分析二次函数的性质;通过探究二次函数的数据来分析二次函数的形状，依形求义，以形表像，形义互补，从而让学生更好的掌握二次函数的知识。

一、以形论数，挖掘隐含条件

二次函数最重要的性质就是对称性，单调性和最值。在学习二次函数的图像的时候，我们从最简单的二次函数y=ax2开始探究，然后通过平移推广到一般的二次函数。二次函数的形状体现了二次函数的开口方向，对称轴的范围，与坐标轴的交点，单调区间，最值的范围等。在观察二次函数的图像的过程中，我们要深刻理解图形所表达出来的意义，同时，挖掘图形所隐含的条件。

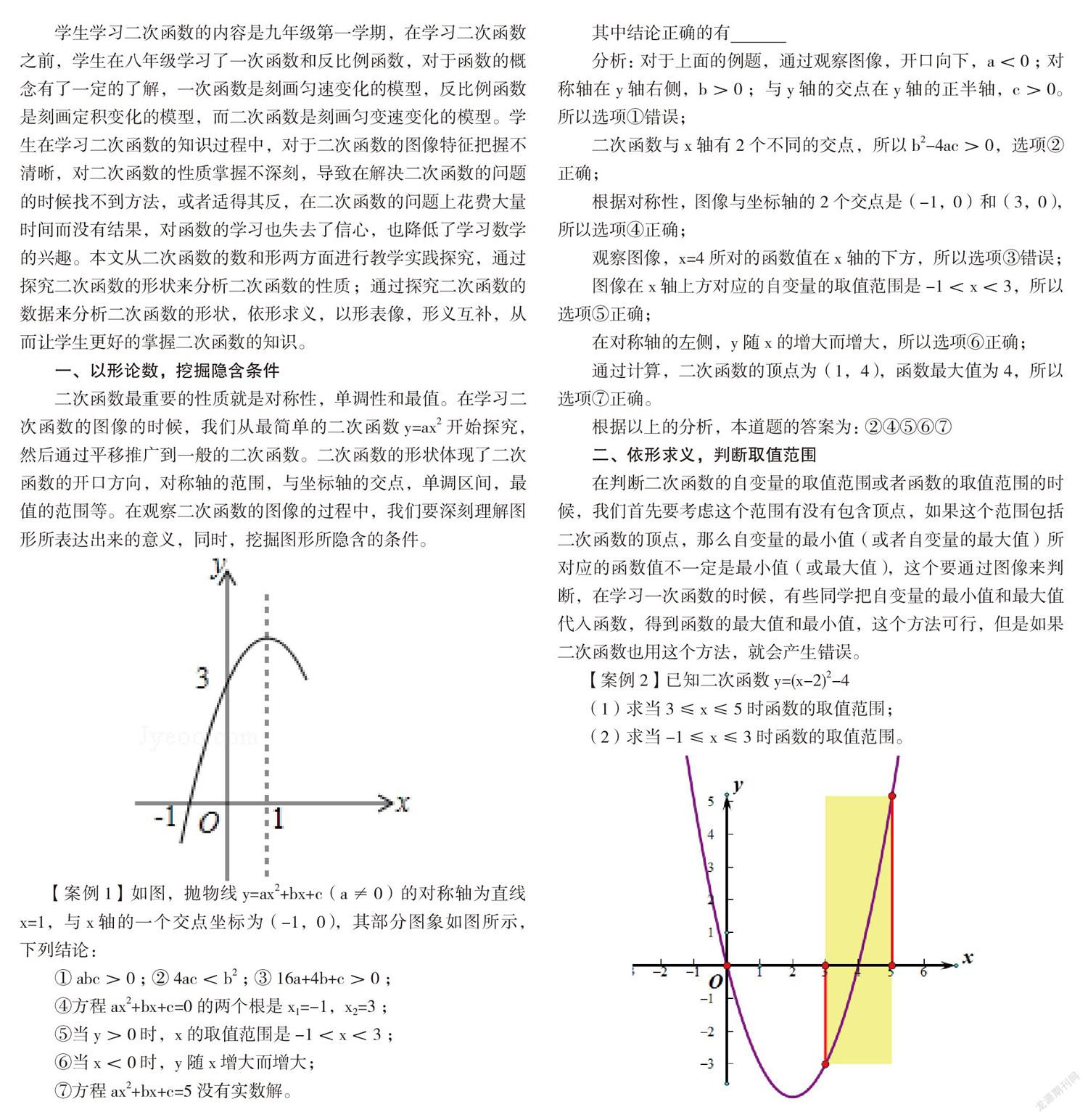
【案例1】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其部分图象如图所示，下列结论：

①abc>0; ②4ac0;

④方程ax2+bx+c=0的两个根是x1=-1，x2=3;

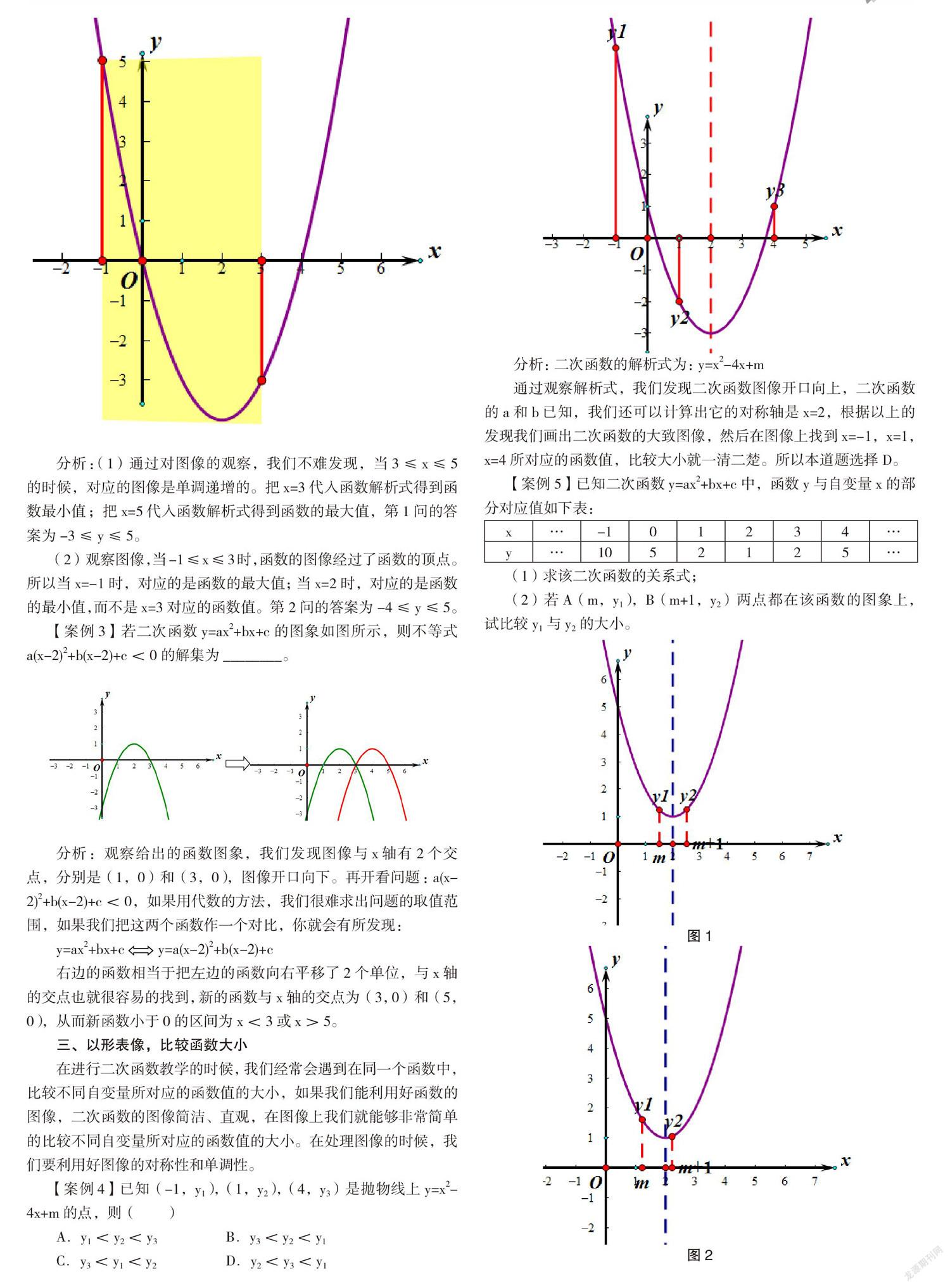
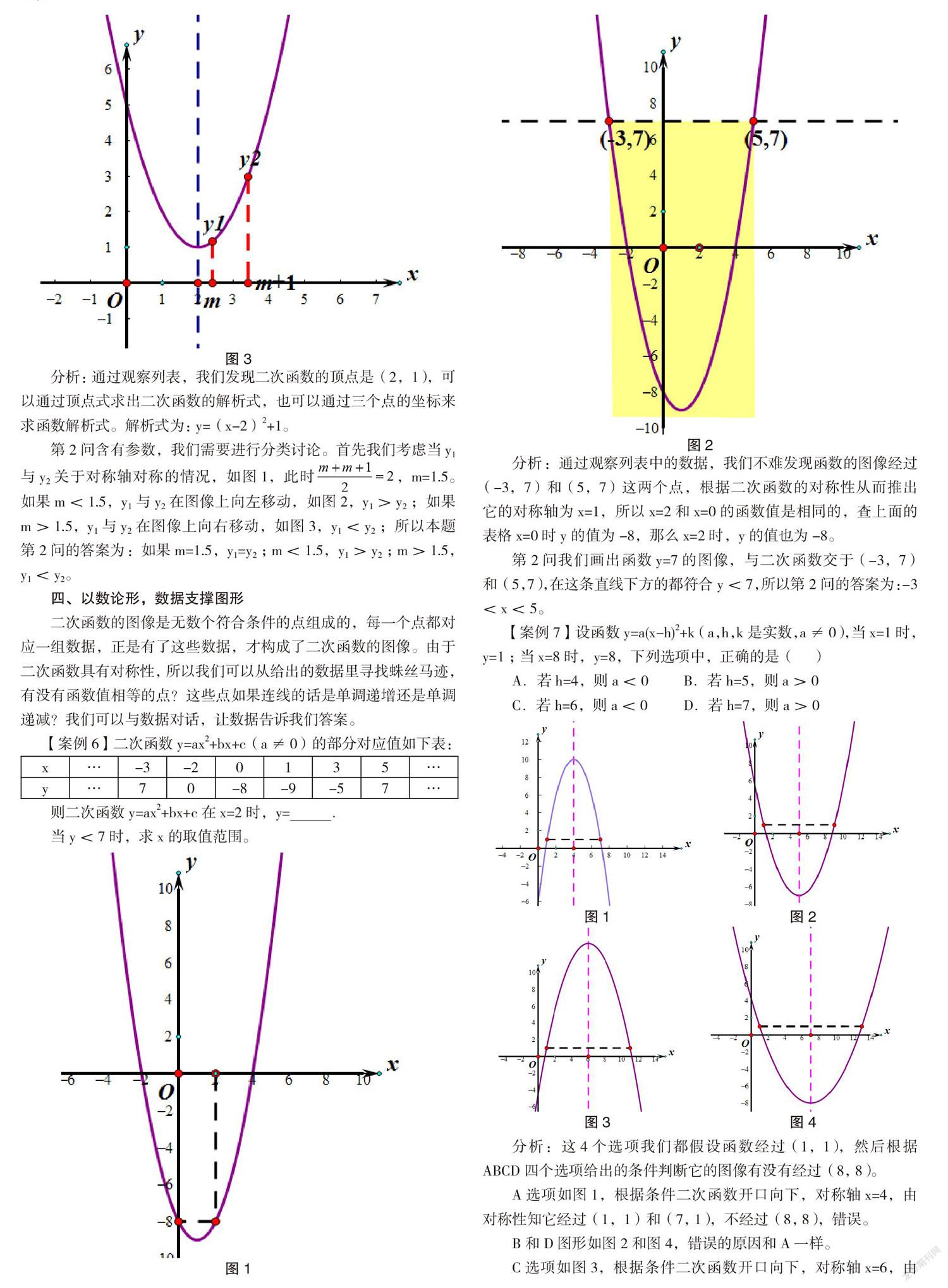
⑤当y>0时，x的取值范围是-1

⑥当x<0时，y随x增大而增大;

⑦方程ax2+bx+c=5没有实数解。

其中结论正确的有

分析：对于上面的例题，通过观察图像，开口向下，a<0;对称轴在y轴右侧，b>0;与y轴的交点在y轴的正半轴，c>0。所以选项①错误;

二次函数与x轴有2个不同的交点，所以b2-4ac>0，选项②正确;

根据对称性，图像与坐标轴的2个交点是（-1，0）和（3，0），所以选项④正确;

观察图像，x=4所对的函数值在x轴的下方，所以选项③错误;

图像在x轴上方对应的自变量的取值范围是-1

在对称轴的左侧，y随x的增大而增大，所以选项⑥正确;

通过计算，二次函数的顶点为（1，4），函数最大值为4，所以选项⑦正确。

根据以上的分析，本道题的答案为：②④⑤⑥⑦

二、依形求义，判断取值范围

在判断二次函数的自变量的取值范围或者函数的取值范围的时候，我们首先要考虑这个范围有没有包含顶点，如果这个范围包括二次函数的顶点，那么自变量的最小值（或者自变量的最大值）所对应的函数值不一定是最小值（或最大值），这个要通过图像来判断，在学习一次函数的时候，有些同学把自变量的最小值和最大值代入函数，得到函数的最大值和最小值，这个方法可行，但是如果二次函数也用这个方法，就会产生错误。

【案例2】已知二次函数y=（x-2）2-4

（1）求当3≤x≤5时函数的取值范围;

（2）求当-1≤x≤3时函数的取值范围。

分析：（1）通过对图像的观察，我们不难发现，当3≤x≤5的时候，对应的图像是单调递增的。把x=3代入函数解析式得到函数最小值;把x=5代入函数解析式得到函数的最大值，第1问的答案为-3≤y≤5。

（2）观察图像，当-1≤x≤3时，函数的图像经过了函数的顶点。所以当x=-1时，对应的是函数的最大值;当x=2时，对应的是函数的最小值，而不是x=3对应的函数值。第2问的答案为-4≤y≤5。

【案例3】若二次函数y=ax2+bx+c的图象如图所示，则不等式a（x-2）2+b（x-2）+c<0的解集为________。

分析：观察给出的函数图象，我们发现图像与x轴有2个交点，分别是（1，0）和（3，0），图像开口向下。再开看问题：a（x-2）2+b（x-2）+c<0，如果用代数的方法，我们很难求出问题的取值范围，如果我们把这两个函数作一个对比，你就会有所发现：

y=ax2+bx+cy=a（x-2）2+b（x-2）+c

右边的函数相当于把左边的函数向右平移了2个单位，与x轴的交点也就很容易的找到，新的函数与x轴的交点为（3，0）和（5，0），从而新函数小于0的区间为x<3或x>5。

三、以形表像，比较函数大小

在进行二次函数教学的时候，我们经常会遇到在同一个函数中，比较不同自变量所对應的函数值的大小，如果我们能利用好函数的图像，二次函数的图像简洁、直观，在图像上我们就能够非常简单的比较不同自变量所对应的函数值的大小。在处理图像的时候，我们要利用好图像的对称性和单调性。

【案例4】已知（-1，y1），（1，y2），（4，y3）是抛物线上y=x2-4x+m的点，则（ ）

A.y1

C.y3

分析：二次函数的解析式为：y=x2-4x+m

通过观察解析式，我们发现二次函数图像开口向上，二次函数的a和b已知，我们还可以计算出它的对称轴是x=2，根据以上的发现我们画出二次函数的大致图像，然后在图像上找到x=-1，x=1，x=4所对应的函数值，比较大小就一清二楚。所以本道题选择D。

【案例5】已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：

x … -1 0 1 2 3 4 …

y … 10 5 2 1 2 5 …

（1）求該二次函数的关系式;

（2）若A（m，y1），B（m+1，y2）两点都在该函数的图象上，试比较y1与y2的大小。

图1

图2

图3

分析：通过观察列表，我们发现二次函数的顶点是（2，1），可以通过顶点式求出二次函数的解析式，也可以通过三个点的坐标来求函数解析式。解析式为：y=（x-2）2+1。

第2问含有参数，我们需要进行分类讨论。首先我们考虑当y1与y2关于对称轴对称的情况，如图1，此时，m=1.5。如果m<1.5，y1与y2在图像上向左移动，如图2，y1>y2;如果m>1.5，y1与y2在图像上向右移动，如图3，y1y2;m>1.5，y1

四、以数论形，数据支撑图形

二次函数的图像是无数个符合条件的点组成的，每一个点都对应一组数据，正是有了这些数据，才构成了二次函数的图像。由于二次函数具有对称性，所以我们可以从给出的数据里寻找蛛丝马迹，有没有函数值相等的点？这些点如果连线的话是单调递增还是单调递减？我们可以与数据对话，让数据告诉我们答案。

【案例6】二次函数y=ax2+bx+c（a≠0）的部分对应值如下表：

x … -3 -2 0 1 3 5 …

y … 7 0 -8 -9 -5 7 …

则二次函数y=ax2+bx+c在x=2时，y=   .

当y<7时，求x的取值范围。

图1

图2

分析：通过观察列表中的数据，我们不难发现函数的图像经过（-3，7）和（5，7）这两个点，根据二次函数的对称性从而推出它的对称轴为x=1，所以x=2和x=0的函数值是相同的，查上面的表格x=0时y的值为-8，那么x=2时，y的值也为-8。

第2问我们画出函数y=7的图像，与二次函数交于（-3，7）和（5，7），在这条直线下方的都符合y<7，所以第2问的答案为：-3

【案例7】设函数y=a（x-h）2+k（a，h，k是实数，a≠0），当x=1时，y=1;当x=8时，y=8，下列选项中，正确的是（     ）

A.若h=4，则a<0 B.若h=5，则a>0

C.若h=6，则a<0 D.若h=7，则a>0

图1 图2

图3 图4

分析：这4个选项我们都假设函数经过（1，1），然后根据ABCD四个选项给出的条件判断它的图像有没有经过（8， 8）。

A选项如图1，根据条件二次函数开口向下，对称轴x=4，由对称性知它经过（1，1）和（7， 1），不经过（8， 8），错误。

B和D图形如图2和图4，错误的原因和A一样。

C选项如图3，根据条件二次函数开口向下，对称轴x=6，由对称性知它经过（1，1）和（11， 1），有可能经过（8， 8），所以选项C正确。

五、形义互补，回归问题本源

二次函数命题的形式比较多，命题者想尽千方百计来考查学生对知识的掌握。面对一些新题型，很多同学感到力不从心。但是如果我们抓住了问题的核心，处理起来就能够得心应手。面对二次函数问题，我们首先分析问题的条件，有些问题是二次函数与其它函数的关系，有些问题是二次函数的对称性问题，有些问题是二次函数的单调性，有些问题是比较二次函数值的大小，知道了解决的问题方向，我们就能够顺着这个方向抽茧剥丝，解决问题。

【案例8】已知a是方程的实数根，则直线y=ax+2-c的图像大致是（    ）

A B

C D

分析：判断直线y=ax+2-a所经过的象限，我们必须知道a的范围。a是方程的实数根，这个根的范围我们如何确定呢？我们可以通过画图像来解决。

假设y1=x2-4x，，在同一个直角坐标系中画出上面2个函数的图像，我们发现它们在第一象限有交点，并且交点的横坐标大于2，所以我们可以判断a>2，那么所求直线y=ax+2-a经过一三四象限，正确答案为A。

【案例9】已知函数y1=x2-（m+2）x+2m+3，y2=nx+k-2n（m，n，k为常数且n≠0）.若函数y1，y2的图象始终经过同一定点M。

（1）求点M的坐标和k的值。

（2）若m≤2，当-1≤x≤2时，总有y1≤y2，求m+n的取值范围。

分析：y1=x2-mx-2x+2m+3，解析式里含有参数m，过定点说明与m无关，解析式可以化为：

（2-x）m+x2-2x+3-y1=0，所以x=2，y1=3，定点是（2， 3）。定点坐标代入一次函数解析式得k=3。

第2问我们利用好图像。二次函数和一次函数都经过了定点（2， 3），二次函数开口向上，由于m≤2，所以对称轴≤2，当-1≤x≤2时，总有y1≤y2，也就是说-1≤x≤2时，y2的图像总在y1的上方，当x=-1时，-1所对的一次函数值大于或等于-1所对的二次函数值即可。根据以上分析可得：

（-1）2-（m+2）（-1）+2m+3≤-n+3-2n，化简后得：m+n≤-1

在二次函数的解答过程中，我们要仔细分析好题目的条件，深刻理解二次函数的数和形的关系，利用好它们的关系，我们可以把复杂问题简单化，综合的问题直观化。在分析二次函数的数与形的时候，我们要把握好关键数据和图像特征，按照以下流程来分析：

综上所述，数形结合是解决二次函数的桥梁，数形结合揭示了二次函数题目知识点之间的内在联系，既分析了代数的意义，又显示了几何直观，使数量的刻画和图形的直观充分融合，教师在实际教学过程中，要培养学生这种思想方法，不仅可以帮助学生更好的理解和掌握知识，还能够发展学生的抽象思维能力，培养学生直观想象能力，从而达到提高学生核心素养的要求。