一种快速有效的正弦波信号频率估计方法∗

温兵会 毛卫宁

(1 东南大学网络空间安全学院 南京 210096)

(2 东南大学信息科学与工程学院 南京 210096)

0 引言

正弦波信号的频率估计是数字信号处理领域的一个值得研究的经典课题，在声呐、雷达等领域应用广泛。采用离散傅里叶变换(Discrete Fourier transform,DFT)谱估计方法估计正弦波信号的频率是一种常用方法，由于快速傅里叶变换(Fast Fourier transform,FFT)算法的高效性，该方法在工程上得到广泛应用[1−3]。利用FFT 谱估计法进行正弦波信号频率估计的方法很多，大体上可以分为两类。一类是需要判别频率修正方向的算法，如Rife算法[4−5]、M-Rife算法[6]和I-Rife算法[7]。Rife算法是正弦信号频域频率估计的经典算法，通过频谱插值对实际频率相对于谱线最大值频率的偏移量进行估计，计算量小，但是存在两个问题：一是当实际频率在谱线最大值频率附近时，频率估计误差相对较大；二是，其频率估计精度易受噪声的影响，低信噪比(Signal-to-noise ratio,SNR)时估计性能下降。M-Rife算法解决了Rife算法的第一个问题，但增加了运算量。I-Rife算法解决了Rife算法的两个问题，但进一步增加了计算量。Rife算法、M-Rife算法和I-Rife算法存在的共同问题是需要判别频率修正方向，再计算频率偏差。另一类，基于FFT的频率估计方法，不需要判别频率修正方向，直接计算频率偏差，如Candan算法[8]、Fang算法[9]和改进的Fang算法[10−12]。Candan算法计算简单，但当信噪比较低时，容易出现插值方向错误，导致误差较大。Fang算法通过对信号在时域补等信号长度的零，采用FFT频谱中最大谱线相邻的两根谱线幅度估计频率偏差，提高了频率估计性能，但增加了计算量。改进的Fang算法在Fang算法基础上提高了频率估计性能，减少了计算量。Candan算法和Fang算法及其改进算法存在的共同问题是涉及到非线性函数的计算，增加了算法的复杂度。为此，本文提出了一种新的频率估计算法，在N点FFT运算基础上，利用两点细化的频谱值估计频率偏移量，分析了频偏估计的偏差和算法的复杂度。相比于I-Rife和改进的Fang算法，本文不需要判别频率修正方向，降低了算法计算量和复杂度。

1 问题描述

含有噪声的复正弦信号为

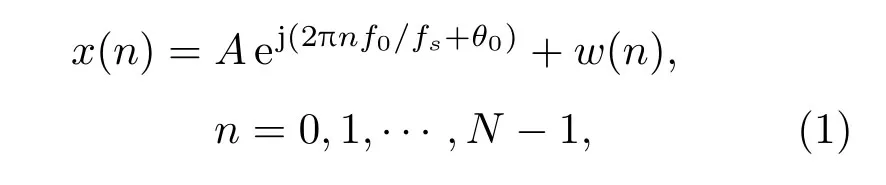
其中，f0=(k0+δ)·∆f为信号频率，∆f=fs/N为频率分辨率，δ为数字频率偏差，取值范围在−0.5∼0.5之间，fs为采样频率，k0为数字频率；w(n)为高斯白噪声，均值为0，方差为A和θ0分别为信号幅度和初相；N为信号长度。

对式(1)所示的信号进行N点DFT得到

式(2)中，W(k)表示高斯白噪声的DFT，在不考虑噪声的情况下信号傅里叶变换的幅值为

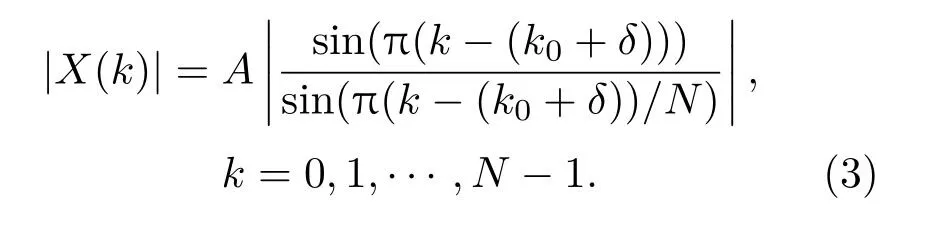
当信号的真实频率不等于频率分辨率∆f的整数倍时，利用FFT 估计频率存在频率偏差，数字频率偏差δ取值范围在−0.5∼0.5之间，信号的真实频率位于谱线最大值与次大值对应的频率之间。

假设信号经过N点FFT 运算后，频谱幅度最大值为|Xk0|，对应的数字频率为k0，次大值为|Xk0+α|。Rife算法利用频谱幅度的最大值和次大值估计频率偏差，频率估计公式为[4]

其中，频率修正方向α=±1。当|Xk0+1| >|Xk0−1|时，α=+1；当|Xk0+1|<|Xk0−1|时，α=−1。

Rife算法计算量小，但在频偏较小时，频率估计误差增大，此外，低信噪比时估计性能下降；I-Rife算法[7]是对Rife算法的改进，利用频谱细化技术计算谱值|X(k0±0.5)|作为频率修正方向的判据，利用频移技术将被估计频率移至两相邻数字频率的中心处，以确保Rife算法能够准确估计频率。I-Rife算法在一定程度上克服了Rife算法的不足，但增加了计算量；改进Fang算法(I-Fang)[10]利用DFT计算6个频点的谱值来估计数字频率偏差，避免了Fang算法中对信号补等长度的零进行2N点FFT运算，减少了计算量，但利用I-Fang算法进行频率估计同样涉及到非线性函数的计算，算法复杂度较高。I-Fang算法性能与I-Rife算法接近，但计算量进一步增大，两者在很低信噪比时，依然存在性能下降和不稳定问题。

2 本文算法和偏差分析

2.1 本文算法

为了提高低信噪比时的频率估计性能，同时减小计算量，本文提出一种快速有效的频率估计方法，运用频谱细化方法计算频谱值|X(k0±0.5)|，利用这两点谱值估计数字频偏，不需要判别频率修正方向，提高了频率估计的稳定性。

根据式(3)，k0点左右相邻两点频谱幅度的比值为

式(5)中由于(π(k−δ)+π(k+δ))/2 =kπ，则|sin(π(k−δ))|=|sin(π(k+δ))|，假设π(k−δ)≪N和π(k+δ)≪N，则由公式(5)可得数字频率偏差估计值：

当k=1时，即利用FFT 频谱中的|X(k0−1)|和|X(k0+1)|值来估计数字频偏δ，对应的表达式如下：

式(7)利用频谱值|X(k0−1)|和|X(k0+1)|计算数字频偏易受噪声的影响，为了提高低信噪比下的频率估计精度，利用频谱细化获得频谱值|X(k0−0.5)|和|X(k0+0.5)|，代入式(6)得到

信号频率的估计值为

本文提出的频率估计算法的流程如下：

步骤1 对采样信号进行N点FFT 运算，寻找幅度谱最大值对应的数字频率k0。

步骤2 利用频谱细化方法计算|X(k0±0.5)|两点谱值。

步骤3 利用式(8)和式(9)估计信号频率。

2.2 偏差分析

本文算法得到的数字频率偏差表示式简单，计算量小，进一步分析表明，还可以得到无噪声情况下频偏的偏差闭合表示式，可用于频率偏差校正，以进一步提高测频精度。

数字频偏δ估计的偏差定义为

根据式(9)和式(10)，频率估计的偏差为

因为数字频率偏差的偏差bδ与频率偏差bf之间的关系是线性的，因此只需分析数字频偏的偏差bδ。

sin(π(0.5+δ)/N)和sin(π(0.5−δ)/N)是关于δ的函数，对其进行泰勒级数展开，在无噪声情况下，根据式(8)和式(10)可得

有噪声时，定义与信噪比有关的数字频偏的偏差为

可以证明，至少存在一个SNR值γ满足bδ(γ)=0。证明过程如下：

根据式(8)和式(13)可得

其中，

根据公式(2)可得

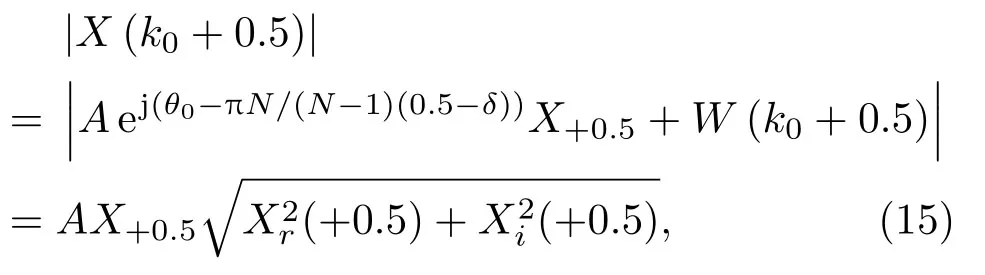
其中，X+0.5=sin(π(0.5−δ))/sin(π(0.5−δ)/N)，W(k0+0.5)表示复高斯噪声。

Wr(k0+0.5)∼N(0,1)和Wi(k0+0.5)∼N(0,1)，因此，可以得到包含高斯随机变量的|X(k0+0.5)|的形式为

其中，K=cos(θ0−π(N−1)/N(0.5−δ))Wr(k0+0.5)+sin(θ0−π(N−1)/N(0.5−δ))Wi(k0+0.5)。

当SNR满足γ →0时，根据式(16)可得

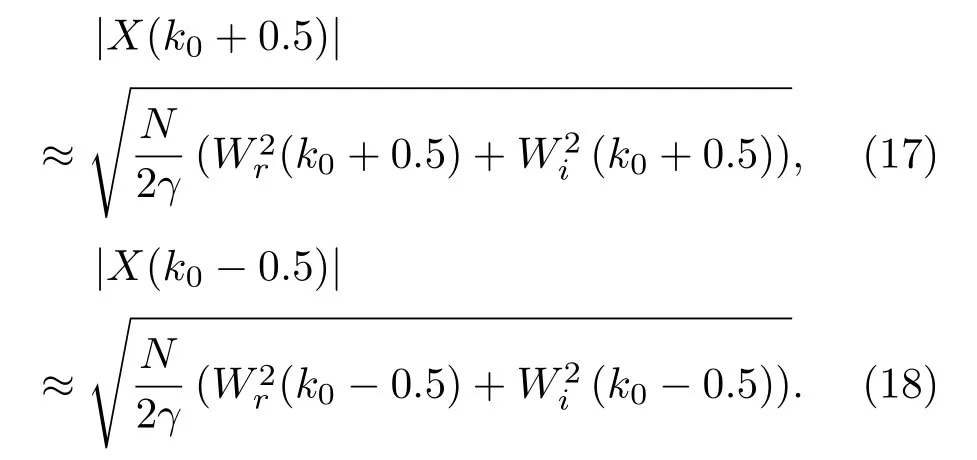
可以证明W(k0+0.5)和W(k0−0.5)是不相关的。Wr(k0+0.5)、Wi(k0+0.5)、Wr(k0−0.5)和Wi(k0−0.5)不相关，且具有相同的分布，则根据式(17)和式(18)可得

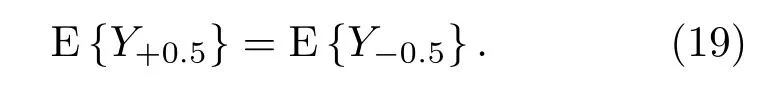
另一方面，当SNR取值满足γ →+∞时，它将近似于无噪声的情况，根据公式(12)，偏差bδ(+∞)和δ有相同的符号。

其中，sgn(·)表示符号函数。如上所述，高SNR和低SNR情况下，偏差的正负号是相反的。因此，存在至少一个SNR值γ0满足bδ(γ0)=0。

3 计算量与性能分析

3.1 仿真实验及性能分析

信噪比定义为SNR =采样频率fs=48 kHz，信号长度N=4800，频率分辨率∆f=fs/N=10∆f=fs/N=10 Hz，信号频率为f0=(256+0.10)∆f/2。对于复正弦信号，在频率、幅度、相位参数均未知的情况下频率估计的克拉美罗界(Cramer-Rao lower bound,CRLB)[9]为

为了验证本文算法的频率估计性能，把本文算法与Rife算法[5]、I-Rife算法[7]、Candan算法[8]和I-Fang算法[10]进行频率估计性能比较。1000次Monte Carlo仿真，信噪比变化范围为−22∼20 dB，数字频偏δ=0.1，本文算法及以上几种算法的频率估计均方根误差和频率估计偏差随信噪比的变化如图1和图2所示。

图1和图2表明，当信噪比大于10 dB时，5种算法频率估计性能接近；信噪比小于10 dB时，Rife算法的频率估计性能最差，Candan算法性能次之，I-Rife算法、I-Fang算法和本文算法估计性能接近。

图1 频率估计均方根误差随信噪比变化Fig.1 Frequency estimation root mean square error varies with SNR

图2 频率估计偏差随信噪比变化Fig.2 Frequency estimation bias varies with SNR

取信噪比SNR =−22 dB，数字频率偏差变化范围为−0.5∼0.5，比较5种算法频率估计的均方根误差随数字频偏的变化，结果如图3所示。本文算法频率估计均方根误差基本上不随频偏变化，较Rife算法有很大的改善，性能与I-Rife算法和I-Fang算法相当。

图3 频率估计均方根误差随数字频偏δ 变化(SNR=−22 dB)Fig.3 Frequency estimation root mean square error varies with digital frequency offset(SNR =−22 dB)

3.2 计算量分析

I-Rife算法除需要一次N点FFT 运算外，还要利用DFT计算4个频点的谱值。I-Rife算法共需要进行(N/2·log2N+ 4N)次复数乘法和(N·log2N+4(N−1))次复数加法。Fang算法共需要进行N·log2(2N)次复数乘法和2N·log2(2N)次复数加法。本文算法要计算一次N点FFT和2个频点的谱值，共需要进行(N/2·log2N+2N)次复数乘法和(N·log2N+2(N−1))次复数加法。改进的Fang算法[10]要计算一次N点FFT和6个频点的谱值，共需要进行(N/2·log2N+6N)次复数乘法和(N·log2N+6(N−1))次复数加法。当N取不同值时，4种算法计算量如图4所示。

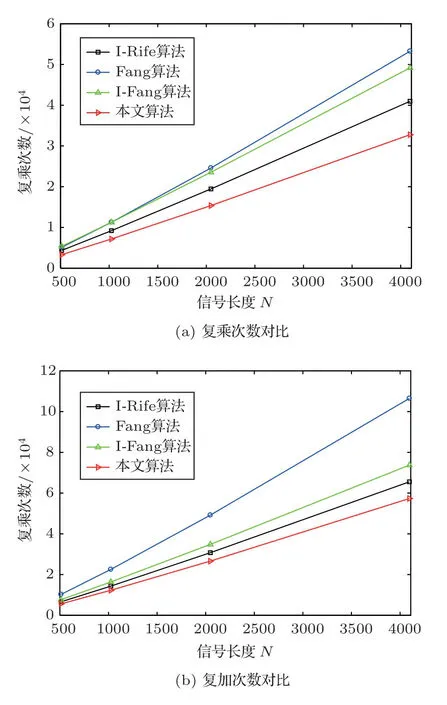
图4 4种算法计算量随信号长度变化Fig.4 The calculation amount of the four algorithms varies with the signal length

图4表明，Fang算法的计算量最大，I-Fang算法的计算量次之，I-Rife算法的计算量再次之，本文算法的计算量最小。随着N取值的不断增大，本文算法的计算量相比I-Rife算法和I-Fang算法更小，更有优势。

4 结论

本文提出了一种利用一次N点FFT和两点细化的频谱值|X(k0±0.5)|精确估计正弦信号频率的方法，分析了频偏估计的偏差和算法计算量。相比于I-Rife和I-Fang算法，本文算法不需要判别频率修正方向，算法复杂度低，计算量小，在保证性能的同时，提高了算法的稳定性和实用性。综上，本文算法的整体性能优于I-Rife算法和I-Fang算法，是一种快速有效的频率估计方法。