一种自对弈棋局学习样例质量评价方法

姬 波，尤惠彬,卢红星，田 欣，2，柳宏川

1(郑州大学 信息工程学院,郑州 450001) 2(郑州大学 产业技术研究所第4代工业研究所,郑州 450001)

1 引 言

计算机棋类游戏被认为是人工智能领域的“果蝇”，对该领域的深入研究有助于理解机器智能中许多基础问题.在计算机棋类游戏中有3个重要里程碑：Chinook、深蓝和AlphaZero，它们分别在西洋跳棋、国际象棋和围棋比赛中取得战胜人类选手的成绩[1]，这对投身该领域研究人员的研究热情起到极大鼓舞作用.

1994年的Chinook基于进化论思想，采用种群中互相博弈和遗传变异的知识传递方式，最终筛选出种群中的最优选手作为优胜者；1997年的深蓝基于向人类专家学习知识的理念构造专家知识库，同时结合α-β剪枝和蒙特卡洛搜索算法解决无法在有限时间内穷举所有可能的国际象棋棋局的问题[2]；2016年的AlphaGo在设计思路上与深蓝极为相似，只不过是从国际象棋转为更复杂的围棋[3]，在很大程度上可认为相较于深蓝，AlphaGo仅仅在计算能力(主要指计算速度)上有所提高；至于AlphaZero则着重强调自学习的概念，强调除下棋规则外没有任何其他领域知识，全程无人工指导[4].

上述3个里程碑从不同角度对“果蝇”进行详细解剖分析，但它们都基于完全一致的认知基础，包括有：

1)承认目前计算机硬件的计算能力有限，无法做到穷举复杂棋局游戏的所有局面.

2)认为人类棋局专家无法表达所有棋局知识，通过建立专家知识库的方式无法解决行棋问题.

3)选用神经网络作为棋类知识的载体(已经证明具有3个隐藏层和足够节点数的神经网络可以模拟任意复杂函数)[5].

4)在训练人工智能选手学习上，通过产生有限学习样例和调整神经网络权重的方法，能够达到准确判断棋局形式的目的.

5)有限的学习样例对所有棋局局面的代表程度，很大程度上决定了人工智能选手的智力高低.

目前即使人工智能选手已经能够战胜人类选手，但棋类人工智能选手身上仍存在很多未能研究透彻的问题.其中一个关键问题是，如何在有限的时间和空间内尽可能产生更多高质量的学习样例.

学习样例生成方式可分为3类：基于已有棋局的专家知识库；基于多选手对弈的遗传变异进化筛选；基于自对弈的蒙特卡洛随机仿真[6].其中，采用依赖专家知识库的方法代价高昂且不宜实现，而采用让人工智能选手间彼此博弈的方法获得学习样例成本低且易于实现.

但目前研究尚且缺乏对于学习样例生成方法和质量评价方法的针对性研究，其主要原因如下：

1)棋类智能研究的目标多聚焦于人工智能选手与其他选手的比赛结果上，尤其是与人类冠军选手的输赢上，将战胜人类选手看作核心研究目标，而对学习样例产生方式及质量评价方法未能引起足够重视.

2)因国际象棋、围棋等众多棋类游戏复杂度较高，生成样例所需的硬件环境不易获得，所以大大挫伤了缺乏条件的研究人员的参与积极性.

3)棋类游戏复杂度高带来的另一个问题是，注意力会更多集中在并行算法(也包括专用硬件的设计)上，力保在计算时间有限的条件下得出相应结果.因此，研究人员对于已经相当成熟的蒙特卡洛仿真或遗传变异算法难以产生足够重视.

4)缺乏明确的定量分析指标，无法建立相应的评价体系.

针对以上问题，本文将研究重心聚焦于学习样例质量评价方法，首次提出采用样本规模综合指标T决定学习样例大小的样例质量评价方法.并在复杂度适中的西洋跳棋游戏中进行验证，借助T指标的指导可以在不降低学习效果的前提下大幅减少学习样例产生的计算成本.

2 博弈树

在博弈类程序设计中，博弈树常作为记录行棋信息的载体，用于记录下棋步骤和棋局信息.为使行棋方在规定时间内搜索到最佳走子方式，采用穷举搜索方法显然不合理，需结合极大极小算法、α-β剪枝算法和蒙特卡洛搜索算法解决该问题[7].

2.1 极大极小算法

Minimax算法又名极小化极大算法，该算法是一个零总和算法，一方选择令自己优势达到最大化的选项，另一方选择令对手优势最小化的选项[8].

本文将“1”看作我方选手，“-1”看作对方选手.因井字棋整棵博弈树无法完整呈现，故只展示博弈树中某一分支，具体搜索过程如图1所示.

根据图1所示的博弈树分支可推断出，在可穷举的情况下采用Minimax算法遍历整棵博弈树，可得到根节点的值，换句话说就是可以找到对当前棋局最有利的情况.

2.2 α-β剪枝算法

在生成博弈树过程中会产生诸多节点，且在实际下棋过程中每步行棋都要在一定时间内完成，因此无法对每个分支都进行访问，可利用α-β剪枝算法解决该问题，通过裁剪搜索树中无意义分支来提高搜索效率.

图1 井字棋整棵博弈树中的某一分支Fig.1 A branch of the whole game tree of TicTacToe

对每个节点来说，假设α为下界，β为上界.任意节点分值N的取值范围为α≤N≤β，α≤β代表N有解；α>β代表N无解.本文规定正方形为我方选手，圆形为对方选手，将极大极小值算法和α-β剪枝算法结合起来，通过不断修改α和β的值判定在何处进行剪枝，某一博弈树剪枝后的最终结果如图2所示.

图2 α-β剪枝结果图Fig.2 Results of α-β pruning

2.3 蒙特卡洛搜索算法

仅使用Minimax算法和α-β剪枝算法无法模拟整个博弈过程，针对无法穷举的情况需结合蒙特卡洛树搜索算法(Monte Carlo Tree Search)，将当前棋局的最优走子方法以一种新颖的方式计算出来[9].即在走子时多次模拟博弈过程，并尝试根据模拟结果预测出一种最优走子策略.

MCTS算法核心思想是从当前棋盘一路向下进行一组随机遍历[10]，其中每次模拟博弈时都需要经过博弈树搜索、节点扩展、随机模拟和反向传播4个步骤.针对博弈树搜索和节点扩展两个重要步骤，画出如图3所示的流程图.

3 学习样例质量的定量评价指标

3.1 西洋跳棋简介

西洋跳棋是一种下棋规则复杂的智力游戏，传统西洋跳棋在8×8的棋盘上进行，其中棋盘上有黑白两种颜色的方块(黑色表示不能放置任何棋子，白色反之)，棋盘左上角为黑色方块且相邻方块不能为同种颜色[11].游戏玩家包括红方选手和蓝方选手，对弈双方各持12个相同颜色的棋子，分别占据棋盘上下两边，如图4所示.

图3 MCTS算法模拟博弈流程图Fig.3 MCTS algorithm simulation game flow chart

图4 西洋跳棋64格棋盘Fig.4 Checkers 64 board

本文规定红方选手为先手，双方轮流下棋.“未成王”棋子只能向对方方向无人占据的斜线空格位置行棋，当棋子到达对方底线时变成“王棋”，随后可向4个斜线方向中任一方向移动.普通棋子在“成王”后不能马上继续吃棋，须等下一回合才可移动.在行棋过程中吃子优先级高于走子，出现连吃情况时连吃优先级高于吃子.

出现下述情况判定该局游戏结束：

1)任意一方玩家的棋子被全部吃完，判定留在棋局上的玩家为获胜方.

2)当棋局上留有双方棋子，但双方选手均无法移动，判定红蓝双方平局.

3)移动步数超过最大限度且仍未分出胜负，判定红蓝双方平局.

3.2 棋盘表示

西洋跳棋在程序中常用表示方法有两种：一种是用二维数组表示棋盘，另一种是用一维数组表示棋盘.由于二维数组表示棋盘更加直观易于分析，综合考虑后认为采用二维数组表示西洋跳棋棋盘更合理.

如图4所示，棋盘位置与二维数组中元素成一一对应关系，例如西洋跳棋棋盘中位置6相当于二维数组中的[1][2]元素.数组元素由{-2，-1，0，+1，+2}组成，以正负号区分红方选手和蓝方选手[12]，其中-2表示蓝王棋、-1表示普通蓝棋、0表示空格(无棋子)、+1表示普通红棋、+2表示红王棋.当普通棋子“成王”后，棋子图像由圆形变为标有“王”字样的圆形，以此来区分普通棋子与王棋.

3.3 棋局学习样例生成

博弈树作为记录信息的载体用于记录行棋信息，将博弈树节点看作是一个棋局状态，博弈树每层均可看作某步行棋后所面临的全部情况[13].

西洋跳棋学习样例生成过程包括棋盘表示、双方迭代自对弈和优化神经网络，一次迭代的整体流程如图5所示.

图5 迭代整体流程图Fig.5 Return to the overall flowchart

每次迭代双方需进行多局自对弈，每局均默认红方先行，且红方选手权重获取方式为文件读取，蓝方选手获取权重方式为随机获得.由于初始局红方无较好的神经网络作为开局选手，因此需根据下述操作获得红方下次迭代的权重信息：在第1次迭代过程中，保存所有红方胜n子(即本局结束后红方获胜，且盘面上红方剩余棋子个数比蓝方剩余棋子个数多n个及以上)的权重信息，在红方胜n子的棋局中随机选取一局，作为红方本次迭代的最优训练结果.

从第2次迭代开始，红方选手读取上次迭代训练完成后存入txt文件的权重信息，将其作为本次自对弈下棋的选手，蓝方选手仍以随机获取权重的方式进行自对弈下棋，值得注意的是每次迭代结束前，红方选手能力(即权重信息)不再发生变化.本次迭代完成后双方对战输赢结果一目了然，本文规定红方向蓝方学习，故保留所有蓝方胜n子棋局的详细下棋步骤及权重信息作为学习样例.之所以保存蓝方胜n子的棋局信息，是因为对于那些“侥幸获胜”的蓝方棋局(即没有胜出n子的情况)，本文认为没有太多学习价值，考虑到时间成本问题，决定只保留蓝方胜n(n=6)子的情况.

一次迭代完成后让红方选手向本次迭代中收集到的所有蓝方胜n子棋局学习，并通过不断学习更新自身权重，具体训练过程在3.4小节进行详细介绍.训练完成后将红方选手的权重信息存入文件中，作为下次迭代的开局选手.

重复迭代上述步骤，以此生成更多高质量的学习样例，同时提升红方选手，整体来看红方选手相较于学习前会有一定程度提升.

3.4 局势评估机制

局势评估机制主要包括评估函数和调整权值两大部分.多方参考资料确定影响棋力因素，得到评估函数[14]，并在此基础上生成训练样例，结合函数逼近算法更新红方权重，以此优化红方选手下棋方式.

3.4.1 评估函数

在计算机博弈问题中，评估函数占有重要地位.评估函数确定搜索到的棋局估值大小，估值越大表示对我方棋类选手越有利[15].从当前面临的棋局考虑，为确定下一步棋子走向，需通过评估函数得到下一步所有棋局估值，根据估值大小选择最有利于自己的棋子走向.

西洋跳棋棋盘状态考虑的影响因素包括红蓝双方普通棋子、王棋和空格的位置.每个棋盘状态用一个二维数组表示，根据本文设定的棋盘表示方法，用二维数组的32个元素(x01、x03、x05、x07、x10、x12,…,x72、x74、x76)代表棋盘上32个可走空格状态，其他32个不可走子空格本文不予表示.

本文以蓝方胜局作为红方的学习对象，即用红方下一步面临的棋局状态(蓝方棋局)和红方权值计算出红方的学习目标.结合棋力影响因素确定原始值和目标值，下列式(1)和式(2)为估值法则：

Score_original=Red_status*w_Red

(1)

Score_goal=Blue_status*w_Red

(2)

式(1)中Score_original表示红方本步棋盘状态原始值，Red_status表示红方本步面临的棋局状态；式(2)中Score_goal表示红方本步棋盘状态目标值，Blue_status表示红方下一步面临的棋局状态(蓝方棋局)；w_Red表示红方本局权重.

原始值与目标值的计算均以当前棋盘32个有效位置作为输入，权重和偏差的初始值通过在[-0.2,0.2]上均匀分布采样产生，以BP神经网络输出标量值作为唯一输出，输出值表示当前棋局状态分值.

本文设置神经网络的第1个隐藏层有5个节点，第2个隐藏层3个节点.以第1个隐藏层节点值的计算方法为例，描述计算过程：

第i个神经元的净输入值Si，由32个输入值分别同到该节点的权重累积和，加上该节点本身阈值得到，公式如式(3)所示.此时净输入值Si经过激活函数f(x)变换后作为该节点的输出yj，公式如式(4)所示.

(3)

(4)

其余节点均采用同样计算方法获得输出值，本文不再一一赘述，直到获得输出标量值为止.

3.4.2 调整权值

学习目标函数的过程被称为函数逼近，调整权值是其中一个非常重要的环节.以棋盘状态、原始值和目标值的估值为训练样例，通过BP神经网络的逆向反馈调整权值[16].

BP算法是一个迭代算法，它的基本思想为：

1)计算每层节点分值和激活值，直至输出层(即信号前向传播)；

2)计算每层节点误差，误差的计算过程是从输出层依次向前推进的(即信号反向传播)；

3)更新参数(其目标为使误差减小).迭代步骤1)和步骤2)，直至满足停止准则终止参数更新(如相邻两次迭代的误差差别很小).

某一训练数据(xi，yi)的代价函数如式(5)所示：

Ei=‖yi-oi‖=∑i(yi-oiL)2

(5)

式中：yi为目标值，oi为神经网络对输入xi产生的原始值(即实际输出)，L为神经元层数，i为第i个神经元.

代价函数仅与权值矩阵和偏置向量有关，通过BP算法反向传播调整参数，使总体代价(即误差)变小.过程大致如下：计算神经网络最后一层输出值误差，从后往前反向计算神经网络每层的错误，并计算权值和偏置项的梯度.当多次迭代后达到预设代价函数最小值时，对应的各个神经元参数(即权值和偏置项)即为本次训练最终参数.

3.5 样本规模综合指标

与学习样本产生规模直接相关的两个定量指标分别是：样例总个数s和重复样本率x=r/s.其中，r为重复样本个数，其统计方法是将棋盘状态完全一致(盘面评分未必相同)的学习样例计数为重复样本.

y增大时会有助提高学习样例质量；而x增加会降低学习效果.因此，本文给出了结合两者的样本规模综合指标T，如式(6)所示：

T=α*y-(1-α)*x

(6)

其中，x=r/s；y=tanh(logs)；α为平衡因子且α∈[0,1].

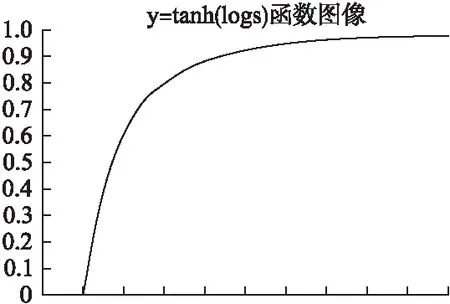
图6 y值随s的变化示意图Fig.6 y value as a function of s

可以看到，T是x和y的线性组合.其中，由于s∈[0,+∞]，故文本对其作了两次变换，首先通过对数log变换降低其数值域，而后通过双曲正切函数tanh变换将值域限定到[0,1].因此，样本规模综合指标T的值域范围为[0,1].其中，y值随s的变化示意如图6所示.

4 实验结果

为验证T指标对学习样例质量的影响，实验中通过设定迭代次数和每次迭代局数两个变量来人为控制棋局规模.

实验1.设定迭代次数和每次迭代局数分别为(100,300)，(300,100)，(100,500)，(500,100)等，其中迭代次数的值为逗号前面的数值；每局迭代局数的值为逗号后面的数值.

表1 不同迭代次数和每次迭代局数下的 样例总个数和重复样本率对比表Table 1 Comparison Table of total number of samples and repeated sample rate under different iterations and rounds per iteration

生成样例中的样例总个数s和重复样本率x如表1所示.

从表1中可得出两个结论：

1)随着整体棋局个数(即迭代次数与每次迭代局数的乘积)的增加，s值也会增加.

2)随着s值增加，x的值虽有小幅度变化，但总体稳定在2%以内.

实验2.设定迭代次数和每次迭代局数分别为(500,1000)，(1000,500)，(2000,300)等，本文给出了每组参数下生成样例中的样例总个数s、重复样本率x、指标值T(a取值为0.8)和用该学习样例数据集训练后的红方AI的胜率情况，如表2所示：

表2 双方自对弈实验结果Table 2 Result of the game experiment

根据表2中数据绘制T值与红方胜率变化组合图，如图7所示.

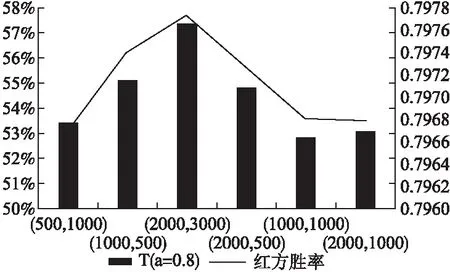
图7 T值与红方胜率变化图Fig.7 T value and red square win rate change chart

图7中横坐标代表迭代次数和每次迭代局数的具体组合情况，左侧数值代表红方胜率，右侧数值代表T值，折线代表红方胜率，长方体代表T值大小.

从表2和图7可得出下列3个结论：

1)迭代次数和每次迭代局数分别为(2000，300)时红方胜率最高，而后随着自对弈次数增加，学习效果反而较差；

2)在平衡参数a取值为0.8时，T值的大小和红方训练后的胜率变化规律一致，这说明在西洋跳棋游戏中T值是一个可以反映学习样例质量的合理指标；

3)采用样本规模综合指标T来决定学习样例大小，可以控制样本规模和学习时间，降低学习成本.

5 结束语

为了在不降低学习效果的前提下大幅降低学习样例产生的计算成本，本文在分析棋盘状态评分方法的基础上，提出采用样本规模综合指标T评价学习样例质量，并在西洋跳棋游戏上进行了验证.

下一步工作包括：验证该指标在其他自对弈棋类游戏学习的指导效果；通过改良实验中的AI选手的神经网络结构来提高学习后的胜率等.