一类具有隔离和治疗措施的新型冠状病毒肺炎(COVID-19)传染病模型研究

闫慧林, 王晓静, 白玉珍

(北京建筑大学 理学院, 北京 100044)

在过去的二十多年里, 出现了一系列由冠状病毒引起的传染病, 如2003年的传染性非典型肺炎(SARS)、2012年的中东呼吸综合征(MERS)等。2019年底至今, 新型冠状病毒肺炎(COVID-19)在中国乃至全世界大流行。截至2021年1月10日, 我国累计确诊病例97 658例,累计死亡病例4 799例; 全球新冠肺炎累计确诊90 714 813例, 累计死亡1 943 597例, 给人们的身体健康和生命安全带来了很大困扰和威胁, 严重影响了全球经济、政治和金融行业的发展[1]。目前尚不确定人们在感染冠状病毒后所获得的免疫能够保持多长时间[2]。

新型冠状病毒肺炎(COVID-19)的症状, 一般包括发热、鼻塞、流涕、咽痛以及最常见的干咳。轻型和普通型患者一般两周左右可以痊愈, 重型的患者可能会出现气促、胸闷、低氧血症, 甚至进展为呼吸衰竭、急性呼吸窘迫综合征、脓毒症休克以及多器官功能衰竭等严重情况, 需要入住ICU进行呼吸支持。一般老年人, 或者有严重基础疾病的患者, 进展到危重型的风险较大, 应该进行早期预警。

为研究COVID-19在人群中的传播情况, 分析影响疾病流行的原因和关键因素, 寻求预防和控制的最优策略, 构建合理的能够刻画COVID-19传播的传染病模型, 并对模型动力学性态进行定性分析和数值模拟, 进而分析疾病的发展过程, 揭示流行规律, 可以为新型冠状病毒肺炎的预防和控制起到指导作用, 具有一定的实际意义和应用价值。

1 模型建立

将我国在COVID-19疫情期间的总人口N分为9个不同的仓室: 易感者(S)、潜伏期感染者(E)、显性感染者(I)、隐性感染者(A)、隔离的易感者(Sq)、隔离的潜伏期感染者(Eq)、入院治疗者(H)、康复者(R)和死亡者(M)。基于目前已有的研究基础[3-8], 为综合考虑隔离和治疗措施对COVID-19传播的影响，做如下假设:

1)人口总数在研究区域内呈均匀分布, 且在传染期内人群总数保持不变。

2)康复者(R)内的治愈者获得免疫不会二次感染。

3)模拟2020年2—5月的疫情情况, 故不考虑人口的出生率和自然死亡率, 并且忽略迁入率和迁出率。

4)潜伏期感染者(E)、显性感染者(I)、隐性感染者(A)的传染力分别为εβ、β、θβ。

由上述假设,建立的仓室模型的流程如图1所示，参数意义见表1。

表1 SEIAHRMSqEq模型的参数意义

其中λ(t)=βc(εE+I+θA)/N，依此构建的模型(1)为：

(1)

2 控制再生数

控制再生数Rc代表1个阈值, 即当环境中都是易感者并且存在治疗措施, 在平均染病周期内具有传染性的1个感染者有效接触易感者后, 导致新增的平均感染人数。当Rc>1时, 疫情一般会继续扩散; 当Rc<1时, 可以认为疫情得到了有效的控制[9-11]。考虑到我国现在严控严防的隔离措施, 因此隔离的易感者Sq、隔离的潜伏期感染者Eq、入院治疗者H在严格的隔离措施下, 不具备继续扩散传染的能力,康复者R获得免疫, 因此在短期内不能再次被感染, 不参与疾病传播, 故只需研究模型(2)：

(2)

模型(2)具有感染力的仓室为E、I、A,模型(2)的无病平衡点P0=(S0,0,0,0)。

由

(3)

(4)

可以算出:

(5)

(6)

(7)

可求出控制再生数为:

Rc=ρ(FV-1)=

(8)

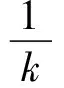
3 稳定性及敏感度分析

定理:如果Rc<1,模型(2)的无病平衡点是局部渐近稳定的;Rc>1时不稳定。

证明:模型(2)在无病平衡点P0的雅可比矩阵[12-13]为:

J|P0=

(9)

由特征多项式(10)：

|λE-J|P0|=

(10)

可得：

λ3+[γI+α+η+γA+k-(1-ρ)φβcε]λ2+

{(γI+α+η)γA+(γI+α+η+γA)[k-

(1-ρ)φβcε]-(1-ρ)φβcpk-

(1-ρ)φβcθk(1-p)}λ+

(γI+α+η)γA[k-(1-ρ)φβcε]-(1-ρ)φβcpkγA-

(1-ρ)φβcθk(1-p)(γI+α+η)=0

(11)

为方便计算,将上面的式子记为：

λ3+p1λ2+p2λ+p3=0

(12)

其中p1、p2、p3分别为：

p1=k(1-R0)+μpk+μθk(1-p)+γI+α+η

(13)

p2=k(1-R0)(γI+α+η+γA)+

(14)

p3=(1-R0)kγA(γI+α+η)

(15)

其中μ=(1-ρ)φβc。

显然当Rc<1时,有p1>0、p2>0并且：

p1p2-p3=k2(1-R0)2(γI+α+η+γA)+

(1-R0)(γI+α+η)γAk+

(1-R0)(γI+α+η+γA)μpk2(1-p)+

(γI+α+η)μθkγA(1-p)+k(1-R0)(γI+α+η)2+

(16)

故由Hurwitz定理可知模型(2)的雅可比矩阵的特征多项式的特征根具有负实部,因此无病平衡点P0是局部渐近稳定的。

当Rc>1时,有p1>0、p2>0和p3=(1-Rc)kγA(γI+α+η)<0,因此可知特征多项式至少有一个特征值是正的,所以无病平衡点是不稳定的。

敏感度分析是了解参数对疾病的影响以及如何控制疾病发展的一种重要方法[14-15]。变量m关于n的敏感度指数定义为:

(17)

将计算Rc对每个参数的敏感度。依次求Rc关于φ、β、θ、ε、c的偏导数,可得：

(18)

(19)

(20)

(21)

(22)

由计算可知,Rc随着φ、β、θ、β、c的增加而增加。由Rc关于ρ、η、k、γA、γI的偏导数：

(23)

(24)

(25)

(26)

(27)

(28)

可发现Rc随着ρ、η、k、γA、γI的增加而减小。

综上所述,Rc随着ρ的增加而减少,当ρ>0.5时Rc对ρ的变化最为敏感,ρ的增加会导致Rc相同甚至更多比例地减少;当ρ<0.5时Rc随着ρ的增加而减少;φ、β、c的增加会导致Rc相同比例地增加。从敏感度分析可知,在传染病传播过程中减少接触率对控制疾病传播有更好的效果。

4 数值模拟

查询2020年2—5月国家卫生健康委员会关于COVID-19的数据[1],可知当下新型冠状肺炎疫情在我国已经得到了较好的控制。

由图2可知，2020年2—5月, 我国新增确诊人数正在逐渐减少，累计死亡人数在长时间内保持不变。

图2 新增确诊人数和累计死亡人数随时间序列

由图3可知，2020年2—5月, 我国累计确诊人数逐渐增加但增幅越来越小，累计治愈人数也在同步增加, 两者间的差距日益缩小, 我国现存确诊人数在逐渐减少, 截至2020年5月31日, 我国现存确诊人数不足100人。

图3 累计确诊人数、累计治愈人数和现存确诊人数随时间序列

由图4可知,Rc随着φ、β、θ、ε的增加而增加,且Rc对β的变化最敏感。

图4 Rc随φ、β、θ、ε的变化趋势

由图5可知,Rc随着η、k、γI、γA的增加而减少, 且Rc对k、γA的变化更敏感。

图5 Rc随η、k、γI、γA的变化趋势

5 结论

本文构建了一类具有隔离和治疗措施的新型冠状病毒肺炎传染病模型,预测了COVID-19的发展趋势,对模型的局部稳定性进行了系统的分析,确定了传染病是否流行的阈值Rc。研究结果表明当Rc<1时,系统的无病平衡点是局部渐近稳定的,即当Rc<1时,疾病会逐渐消失;当Rc>1时,疾病会持续传播。

基于对模型(2)的控制再生数Rc和无病平衡点P0的灵敏度分析和数值模拟结果, 可知传染率系数β和接触率c对疫情的传播起到了至关重要的影响。通过媒体宣传教育等各种手段提醒民众注意个人卫生清洁, 加强自我防范意识, 减少非必要外出活动, 切断传播途径，能够有效地降低疫情传播能力进而达到防控的目的。